一文了解模型量化中的QAT和PTQ
由于前一段时间在做模型的转换工作,实际部署的时候需要一些模型加速的方法,常用的有各家的inference框架,如mnn,tnn,tensorrt等,这些框架除了fp32精度外,都支持了int8的精度,而量化到int8常常可以使我们的模型更小更快,所以在部署端很受欢迎。
常用的模型量化方式有训练中量化,QAT,和训练后量化,PTQ,之前转trt时,用的就是PTQ,在一些常用的模型上表现还不错,几乎没有什么掉点,但是在复杂模型,如带有swish的模型啊,或者nas搜出来的模型,表现就不尽人意了,主要是这些模型的参数分布比较奇怪或者是激活值分布没有很强的规律,导致量化失效。而QAT则避免了这一问题,通过在训练过程中去缩小这种误差,可以达到更好的性能。下面大概介绍一些这两种方法。
PTQ
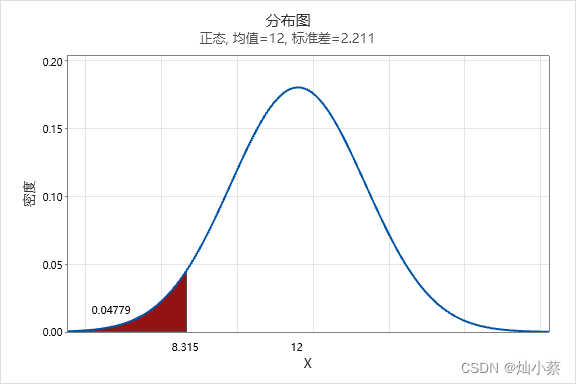
首先是PTQ,以tensorrt的Int8量化为例,它的原理是什么呢,简单概括就是对于常用的模型,如googlenet,resnet等,图片经过网络生成的特征图的值往往具有相同的规律。如下图所示:

图中的绿点表示很多张图的统计结果,所以我们可以看出对于同一模型,任意图的特征激活值都呈现了低激活值高密度的特点,而比较大的那些值所占的比例微乎其微,可以忽略不计,根据这个特点,我们在量化时就不用使用饱和量化(将激活值最大值映射到127),而是人为设计一个阈值,这个阈值可以比最大值小,而刚好可以把高密度区保留,所以trt的int8量化就是在做这样一件事,找阈值s!具体怎么做的呢,那就是一一统计,先将每层特征图的激活值分到2048个bins(按照激活值最小最小区间划分),然后从第127个bin开始尝试设计阈值,什么意思呢,就是先把第128个bin的中间值当为阈值,再把129bin当阈值,一直尝试到2048,每次试阈值时,会把这个阈值映射到127,然后低于这个阈值的元素按照这个计算量化结果,而高于阈值的元素直接归到127(实际在做的时候,看了一些代码实现,都是直接将n个bin分到128个量化值上),由此可以得到一个128维的分布向量,表示每个量化值的元素个数,此时我们要做一件事,就是把这个128维的分布向量和原来的n个bin做相似度计算(分布长度不一样,而且n个bins最后一个bin里边包含尾部所有个数,而128维向量最后一维则不含尾部的。这里有一个trade-off:如果n取得比较小,比如就是128,那么对于非尾部的(<=128)bin,就会和128位向量分布一模一样,但是加上尾部个数后,就会在最后一位分布概率上造成较大的误差,导致相似度降低;如果n取得较大,那么虽然尾部的个数已经比较小了,但是前n个bin的数量较大,导致量化成128维时信息损失较多,从而相似度较低),分布的相似度有很多方法,这里使用kl散度,相似度越高,说明阈值取得越合理,量化的误差也就越小。所以,通过多个阈值的尝试,最后找到误差最小的那个阈值作为scale保留。
注意上面说的是特征图的量化,tensorrt int8量化包含特征图的量化和权重的量化,权重的量化可以缩小模型大小,那么权重是怎么量化的呢,权重的话很简单,就是饱和量化,因为权重的分布比较均匀,所以以最大值映射到127就可以了。
量化好模型后,我们可以得到这么一些参数,首先是权重的int8值,然后是特征图的scale,还有权重的scale,权重的scale是channel-wise的,而特征图则是一层一个。
然后便是,模型的推理了,在模型推理过程中有一个细节,就是,只有kernel内的运算是int8,什么意思呢,就是我们将激活值和量化到int8,和int8的权重做运算,得到结果,这个结果还要反量化回fp32,不然会溢出,再加上bias,最后经过激活,再量化为int8。有人说,则不还是有fp32的运算吗,是的,但是这里可以优化,相较于直接的fp32运算要快得多。
QAT
接着讲QAT,我们在讲PTQ时已经知道,量化过程其实就是在做一件事,就是找阈值 ,或者scale,在PTQ中,我们是通过统计的方法,然后人工通过一些分布相似性得到的,然而,这肯定是有误差的,比如在bin的设计上面,2048只是一个超参。而且,由于量化是每层独立进行的,所以每层的量化是不依赖于前一层量化的结果的,这就导致了在实际的inference过程中会出现误差累积的情况,进一步影响量化后的性能。所以,我们需要一种可学习的scale。QAT就是在做这样一件事情。
这里讲的较详细这个连接讲得比较通俗易懂。
简单概括就是,我们在网络训练过程去模拟量化,我们通过设定一个可学习的scale,这个scale一般可以与weights或者激活值相绑定,然后我们利用一个量化过程 q = round(r/s)*127,将需要量化的值量化到0-127之间,再接着一个反量化过程q * s,就实现了一个误差的传递,接着我们利用反量化后的结果继续前传,最后得到loss,我们求量化后权重的梯度,并用它来更新量化前的权重,使得这种误差被网络抹平,让网络越来越像量化后的权重靠近,最后我们得到了量化后的权重q和缩放因子s。而这一系列操作都可以写成网络中的一个op,实现网络的正常训练。
最后,我们利用q和s,来进行inference。