数据结构–拓扑排序
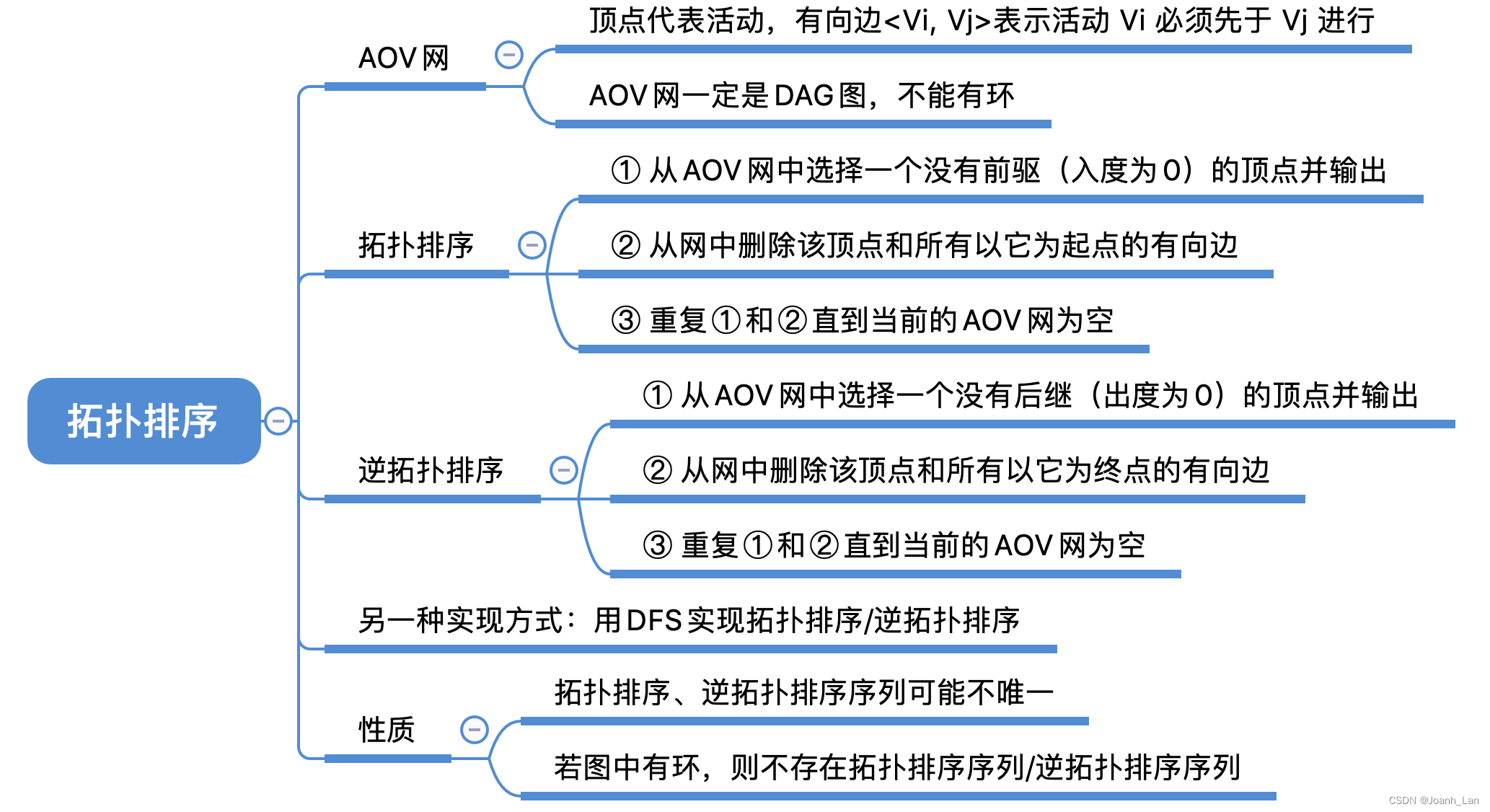
AOV⽹
A O V ⽹ \color{red}AOV⽹ AOV⽹(Activity On Vertex NetWork,⽤顶点表示活动的⽹):
⽤ D A G 图 \color{red}DAG图 DAG图(有向⽆环图)表示⼀个⼯程。顶点表示活动,有向边 < V i , V j > <V_i, V_j> <Vi,Vj>表示活动Vi必须先于活动 V j V_j Vj进⾏
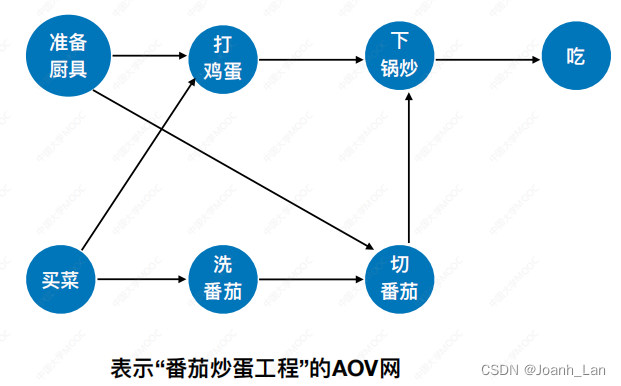
注:如果图中存在环路就不是 A O V 网 \color{red}注:如果图中存在环路就不是AOV网 注:如果图中存在环路就不是AOV网
DAG图是指有向无环图(Directed Acyclic Graph),是一种有向图的特殊形式。它由一些有向边连接的节点组成,并且不存在任何形式的环。换句话说,从任何一个节点出发,沿着有向边的方向无法经过一系列的节点再回到原始节点。DAG图常用于表示一些具有依赖关系的任务或事件,其中每个节点表示一个任务或事件,有向边表示任务或事件之间的依赖关系。DAG图在计算机科学和工程中有广泛的应用,例如任务调度、编译器优化、数据流分析等领域。
拓扑排序
拓扑排序 \color{red}拓扑排序 拓扑排序:在图论中,由⼀个 有向⽆环图 \color{red}有向⽆环图 有向⽆环图的顶点组成的序列,当且仅当满⾜下列条件时,称为该图的⼀个拓扑排序:
① 每个顶点出现且只出现⼀次。
② 若顶点A在序列中排在顶点B的前⾯,则在图中不存在从顶点B到顶点A的路径。或定义为:拓扑排序是对有向⽆环图的顶点的⼀种排序,它使得若存在⼀条从顶点A到顶点B的路径,则在排序中顶点B出现在顶点A的后⾯。每个AOV⽹都有⼀个或多个拓扑排序序列。
上图其中一个拓扑排序:

拓扑排序的实现:
① 从AOV⽹中选择⼀个没有前驱的顶点并输出。
② 从⽹中删除该顶点和所有以它为起点的有向边。
③ 重复①和②直到当前的AOV⽹为空或当前⽹中不存在⽆前驱的顶点为⽌。
注:拓扑排序序列可能有多个 \color{red}注:拓扑排序序列可能有多个 注:拓扑排序序列可能有多个
拓扑排序代码实现
王道书上代码



个人code
#include <iostream>
#include <cstring>
using namespace std;
const int N = 100010;
int n, m;
int h[N], e[N], ne[N], idx;
int q[N], d[N];
void add(int a, int b)
{e[idx] = b;ne[idx] = h[a];h[a] = idx++;
}
bool topsort()
{int tt = -1, hh = 0;for(int i = 1; i <= n; i++)if(!d[i])q[++tt] = i;while(hh <= tt){int t = q[hh++];for(int i = h[t]; i != -1; i = ne[i]){int j = e[i];d[j]--;if(!d[j]) q[++tt] = j;}}return tt == n - 1;
}
int main()
{cin >> n >> m;memset(h, -1, sizeof(h));for(int i = 0; i < n; i++){int a, b;cin >> a >> b;add(a, b);d[b]++;}if(topsort()){for(int i = 0; i < n; i++)cout << q[i] << ' ';cout << endl;}else cout << "-1" << endl;return 0;
}
判断是否存在拓扑序
时间复杂度 O(n + m), n 表示点数,m表示边数
bool topsort()
{int hh = 0, tt = -1;// d[i] 存储点i的⼊度for (int i = 1; i <= n; i ++ )if (!d[i])q[ ++ tt] = i;while (hh <= tt){int t = q[hh ++ ];for (int i = h[t]; i != -1; i = ne[i]){int j = e[i];if (-- d[j] == 0)q[ ++ tt] = j;}}// 如果所有点都⼊队了,说明存在拓扑序列;否则不存在拓扑序列。return tt == n - 1;
}
逆拓扑排序

对⼀个AOV⽹,如果采⽤下列步骤进⾏排序,则称之为 逆拓扑排序 \color{red}逆拓扑排序 逆拓扑排序:
① 从AOV⽹中选择⼀个没有后继( 出度为 0 \color{red}出度为0 出度为0)的顶点并输出。
② 从⽹中删除该顶点和所有以它为终点的有向边。
③ 重复①和②直到当前的AOV⽹为空。
其中一个逆拓扑排序

逆拓扑排序代码实现

逆拓扑排序的实现(DFS算法)

DFS判断是否有环:
int vis[N], cnt; // timestamp
int per[N];
bool cyc[N];// 标记
void dfs(int u) //找环 & 标记环
{vis[u] = ++cnt;for (auto v : g[u]){if (per[u] == v)continue;if (!vis[v]){per[v] = u;dfs(v);}else if (vis[u] > vis[v]){for (int i = u; i != v; i = per[i])cyc[i] = true;cyc[v] = true;}}
}
如果单纯判断是否有环,只需要引进父结点(fa)
dfs(u,fa)
如果 u == fa 则存在环
知识点回顾与重要考点