随着计算机硬件的升级与性能的提高,运算量已不再是阻碍深度学习发展的难题。卷积神经网络(Convolution Neural Network,CNN)是深度学习中一项代表性的工作,CNN 是受人脑对图像的理解过程启发而提出的模型,其雏形是 1998 年 LeCun 提出的 LeNet-5 模型。如今,卷积神经网络已被广泛应用于计算机视觉领域。本文主要介绍卷积神经网络中几个基础的运算,包括卷积、池化与全连接。
目录
1 卷积
2 池化
3 全连接
1 卷积
卷积神经网络中的卷积运算,通常指应用于处理图像的二维卷积。卷积运算是卷积神经网络(Convolution Neural Network,CNN)中不可缺少的部分,使得神经网络具备处理图像的能力。
在介绍卷积运算之前,需要了解卷积运算涉及的几个必要的概念。
(1)卷积核。卷积核通常是一个 3 x 3,或 5 x 5 大小的矩阵,矩阵的元素表示邻近像素值的权重。在卷积运算时,卷积核与图像中某个小区域(也叫局部感受野)的像素值进行加权平均运算。
(2)填充。填充是指处理输入特征图边界的方式。为了不丢失边界信息,可以对输入图像进行边界填充,再执行卷积操作。
(3)步长。步长指卷积核在输入图像上移动的像素数。步长为 1,则每次移动一个像素;步长为 2,则每次移动两个像素;以此类推。
对于输入图像 P,使用 3 x 3 卷积核进行卷积运算,运算步骤如下:
(1)用 0 对图像 P 的边界进行填充,得到扩充图像 P_padding;

(2)按照从上到下、从左到右的顺序,在 P_padding 上移动卷积核,计算像素值的加权平均值,并按照移动的顺序排列,得到输出特征图。

TensorFlow 中使用 tf.nn.conv2d 函数进行卷积运算。
tf.nn.conv2d 用法
tf.nn.conv2d(input,filter,strides,padding,data_format='NHWC',dilations=None,name=None
)tf.nn.conv2d 示例
import numpy as np
import tensorflow as tfx_in = np.array([[[[1], [2], [1]], [[1], [2], [1]],[[1], [2], [1]],
]])kernel_in = np.ones((1,9)).reshape(3, 3, 1, 1)x = tf.constant(x_in, dtype=tf.float32)
kernel = tf.constant(kernel_in, dtype=tf.float32)x_feature = tf.nn.conv2d(x, kernel, strides=[1,1,1,1], padding='SAME')
x_feature.numpy().reshape(3, 3)Spyder 运行结果

一个卷积核只能生成一张特征图像,在实际应用中,为了增强卷积层的表示能力,会使用多个不同的卷积核进行卷积运算,得到若干特征图像。
2 池化
“池化” 一词来源于其英文 pooling,意思是 “使 ...... 集中”。在卷积神经网络中,池化是降低特征图像分辨率的运算,在神经网络中起到二次提取特征的作用。
常用的池化运算有:
(1)最大池化:对局部感受野中的像素值求最大值,作为输出特征图像对应位置的像素值;
(2)平均池化:对局部感受野中的像素值求平均值,作为输出特征图像对应位置的像素值。
下图是对输入图像进行 2 x 2 最大池化的输出结果。

TensorFlow 常用的池化运算如下:
(1)tf.nn.max_pool2d 最大池化
(2)tf.nn.avg_pool2d 平均池化
tf.nn.max_pool2d 用法
tf.nn.max_pool2d(input,ksize,strides,padding,data_format='NHWC',name=None
)tf.nn.max_pool2d 示例
import tensorflow as tfx = tf.constant([[[[4], [6], [1], [3] ], [[0], [9], [7], [13]], [[4], [3], [7], [10]], [[1], [0], [3], [8] ],
]])result = tf.nn.max_pool2d(x, ksize=(2,2), strides=(2,2), padding='SAME')
result.numpy().reshape(2, 2)Spyder 运行结果

3 全连接
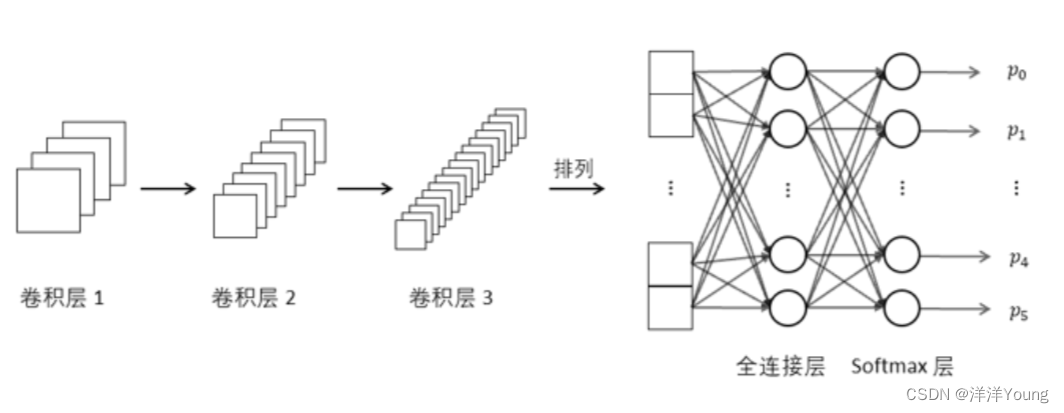
与多层感知机类似,全连接层中的每个神经元与前一网络层中的所有神经元相连。在卷积神经网络中,多个卷积层和池化层后连接着一个或者多个全连接层,全连接运算负责融合卷积层或池化层的局部信息。





![【CTF-web】buuctf-[极客大挑战 2019]EasySQL 1(sql注入)](https://img-blog.csdnimg.cn/0dbcd2b8106847b8a69a2a8731f09877.png)