多变量方差分析：是对多个独立变量是否受单个或多个因素影响而进行的方差分析。它不仅能够分析多个因素对观测变量的独立影响，更能够分析多个因素的交互作用能否对观测变量产生影响。本章以单因素多变量分析为例，即一个分组变量和多个欲分析的变量。

适用条件

各样本是相互独立，满足正态性

满足方差齐性

样本量足够大

对方差齐性的判断通常采用方差齐性检验，实际上只要各组样本含量相等或相近，即使方差不齐，方差分析仍然稳健且检验效能较高。

   在统计软件SPSS中，给出了两种方差齐性检验的方法——Bartlett χ2 检验和Levene检验。相比之下，后者更稳健，且不依赖资料的分布类型。

案例分析

        某研究人员为了解甲 、乙、丙三地男童身体发育情况，在三地分别随机调查了30名8岁男童的身高（cm）、体重（kg）、胸围（cm）指标。

问题：欲分析男童的身体发育是否相同？？

数据视图

 

问题分析：

待分析的因变量为身高、体重、胸围，且均为连续型变量；自变量为地区，分类变量；

手把手教你

【1】分析——一般线性模型——多变量

 

【2】弹出如下所示对话框，将待分析的变量选入“因变量”中，“地区”选入“固定因子”

 

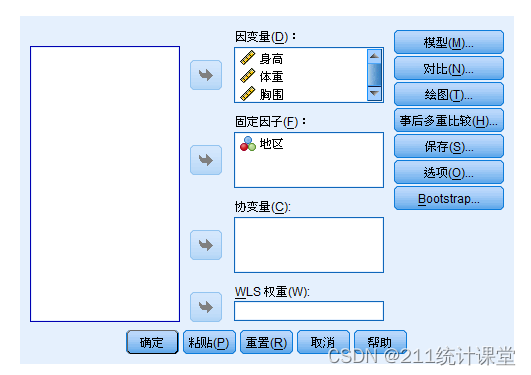
【3】模型（M）——定制，构建类型为“主效应”，选中地区

 

【4】选项——勾选“描述统计”，“同质性检验”  其它统计量可自行选择

 

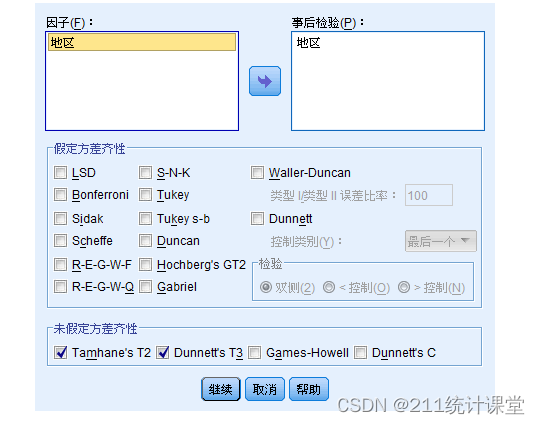
【5】事后多重比较——将地区选入检验框，勾选“未假定方差齐性”的相应检验方法（因为事先已知不满足方差齐性）。

 

结果解析

①描述统计

 

②Levene‘s 方差齐性检验，从结果来看，只有身高满足方差齐性；但仍然可以采用方差分析（因为三组样本含量相等）。

 

③多变量检验

SPSS中给出了四种检验方法，一般选用“Pillai's  Trace”，此法相对较稳定。由结果可知，地区（F=10.983，P<0.001），三地8岁男童的身体发育状况有统计学意义。

 

④主体间效应的检验

身高（F=17.7，P<0.001），体重（F=8.210，P=0.001），胸围（F=17.436 ，P<0.001），可以认为三地2012年8岁男童的身体发育不全相同。

 

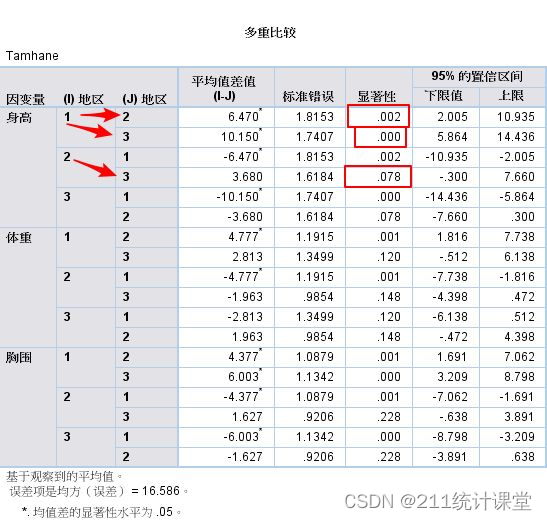
⑤多重比较

以身高为例，检验方法为Tamhane ，检验水准α = 0.05 ，地区甲与乙（P=0.002）和 甲与丙（P<0.001）存在统计学差异 , 乙与丙（P=0.078>0.05）无统计学意义。