部分资料取自于b站：数学建模学习交流清风老师

定义：

• TOPSIS法可翻译为逼近理想解排序法，国内常简称为优劣解距离法
• 它是一种常用的综合评价方法，其能充分利用原始数据的信息，其结果能精确地反映各评价方案之间地差异。

举个例子： 数学成绩越高代表学习能力越强。跑100米花费的时间越少代表体育天赋越好。那怎么样结合这两项不同单位的指标进行综合考量通过打分，得出一名学生最后的得分呢？这就需要使用TOPSIS法，它一般用于已知数据。

问题引入：

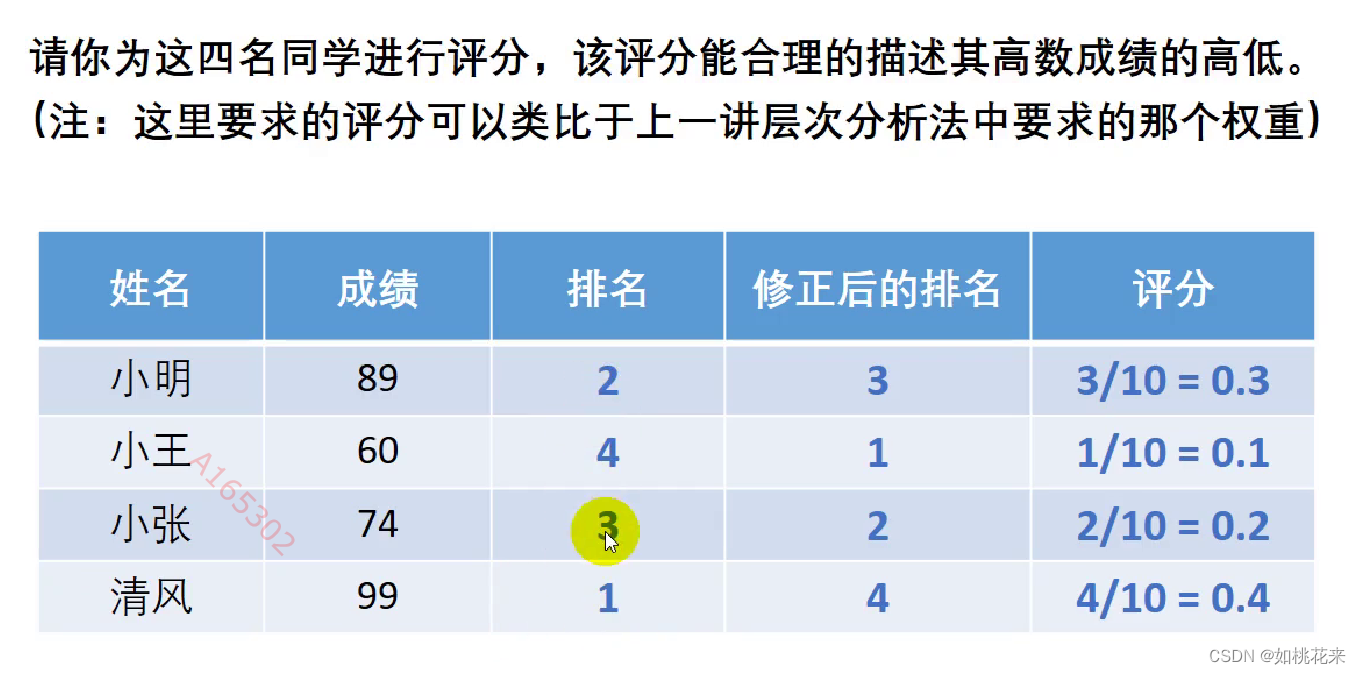
我们需要对一个学生进行评分，成绩越高打的分数自然越高。但是排名数字是从低到高开始的。所以我们需要修正，让修正后的排名数字大小能反映各个学生的评分。如第一名得4分，最后一名得1分。然后进行归一化处理，处理后的评分相加应为1

不合理之处：

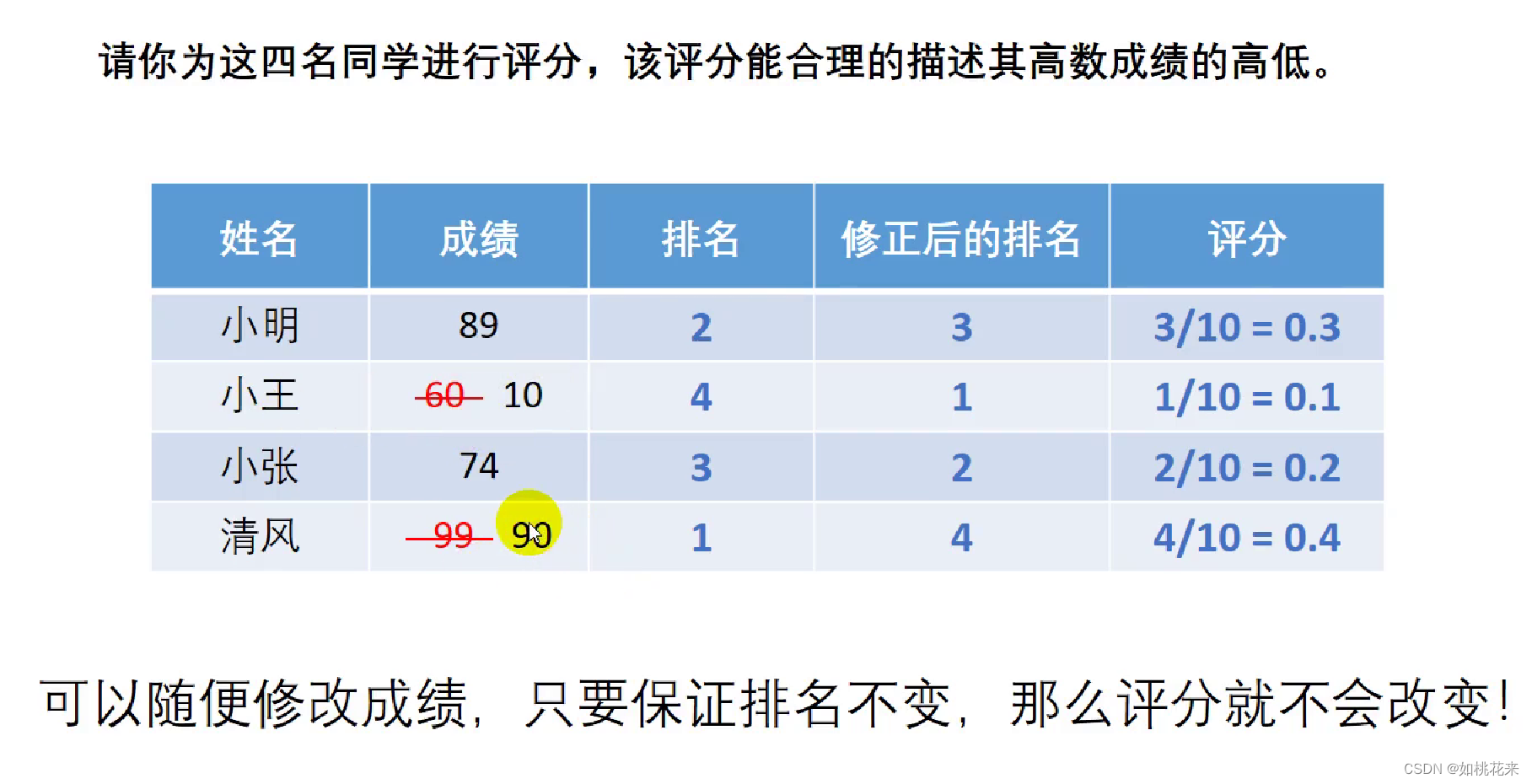
如图所示：按照这种方法进行评价的话。成绩大小可以随意修改，只要不影响排名。这样的话，就会有失合理性。

进行修改：

我们想让成绩的具体分数影响最后的得分，这就必须要引入最高成绩和最低成绩了。通过这两个极值来构造计算评分的公式

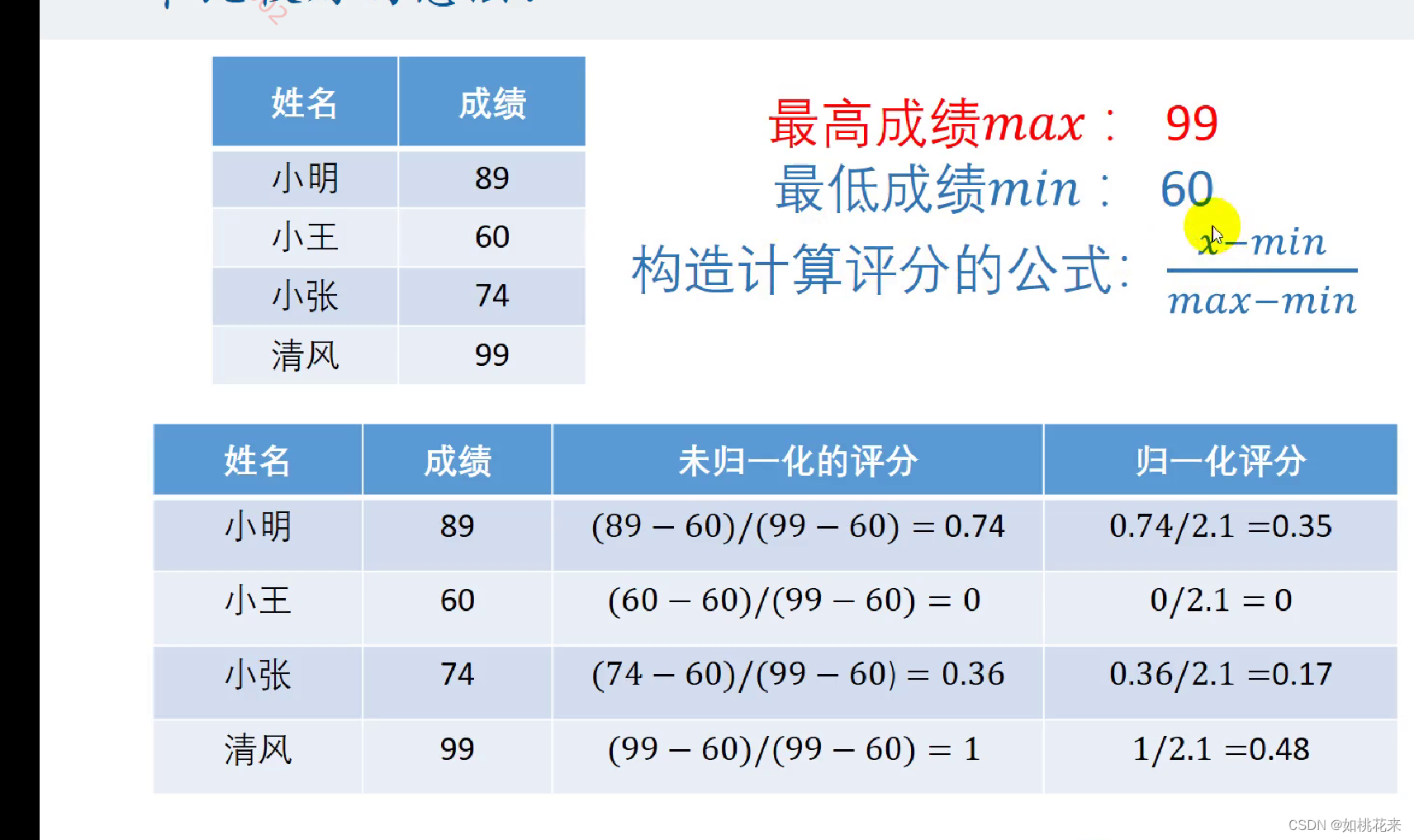
改造后的评分未经过归一化处理时：最高分为1，最低分为0。不用担心0这个数字或者1这个数字过于特殊。实际上，指标通常都在两个以上，综合下来不会出现0和1这种极端情况

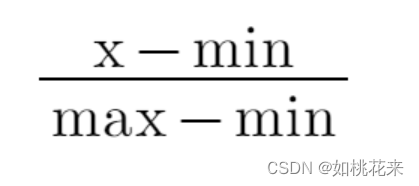
指标分类：

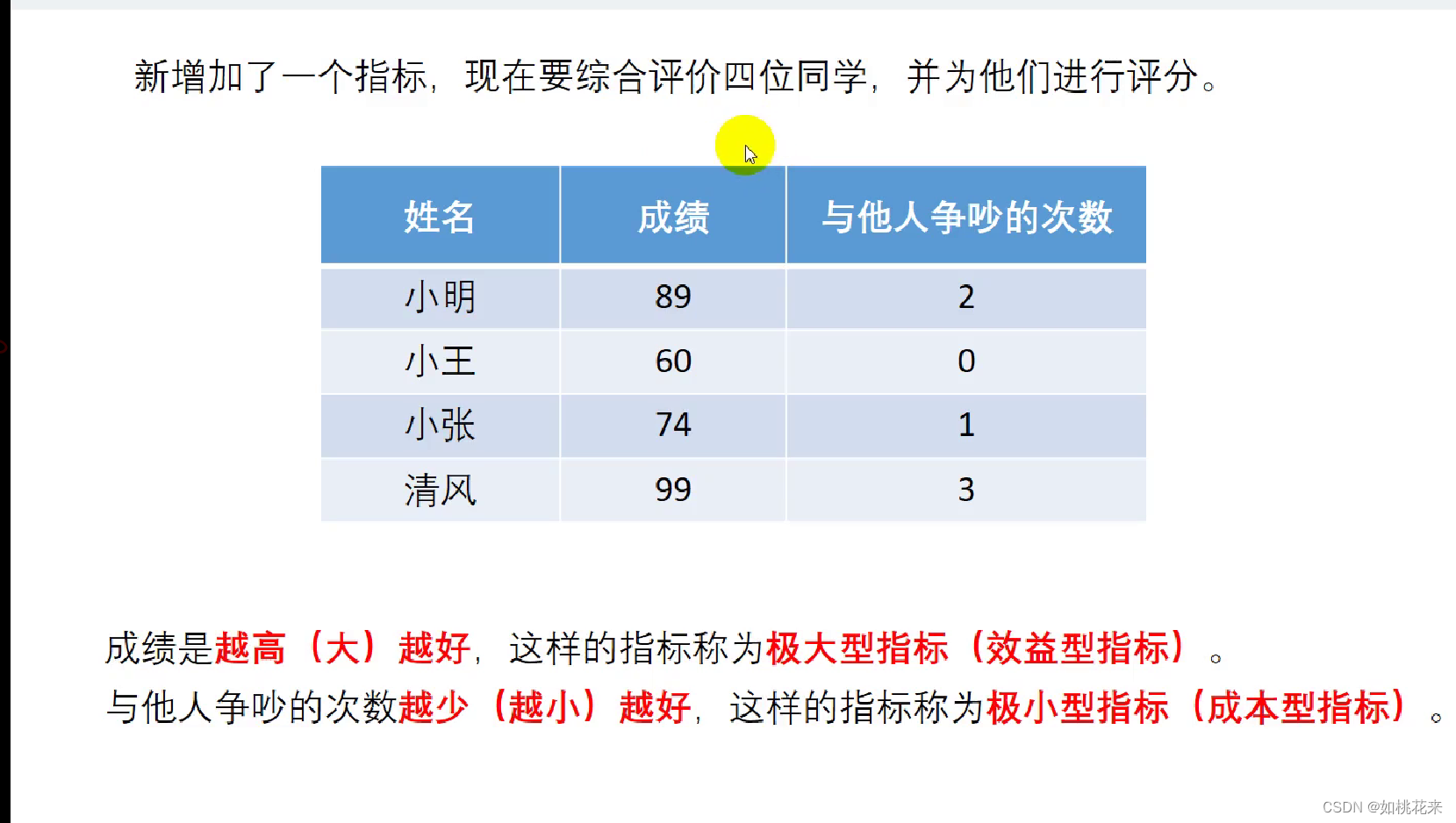
这两个指标一个是越大越好，一个是越少越好。这样的指标就存在分类

常见指标：

1. 极大型指标(效益型指标)：数值越大(多)越好。例子：利润
2. 极小型指标(成本型指标)：数值越小(少)越好。例子：费用
3. 中间型指标：越接近某个值越好。例子：PH值
4. 区间型指标：落在某个区间内最好。例子：体温

指标正向化：

极小型指标正向化公式：

根据上图指出的两个指标来看，成绩越高越好。争吵次数确实越少越好。一个高，一个低不利于进行综合评判。所以我们就需要将所有的指标正向化处理全部化为==极大型指标。==包括中间型指标和区间型指标。

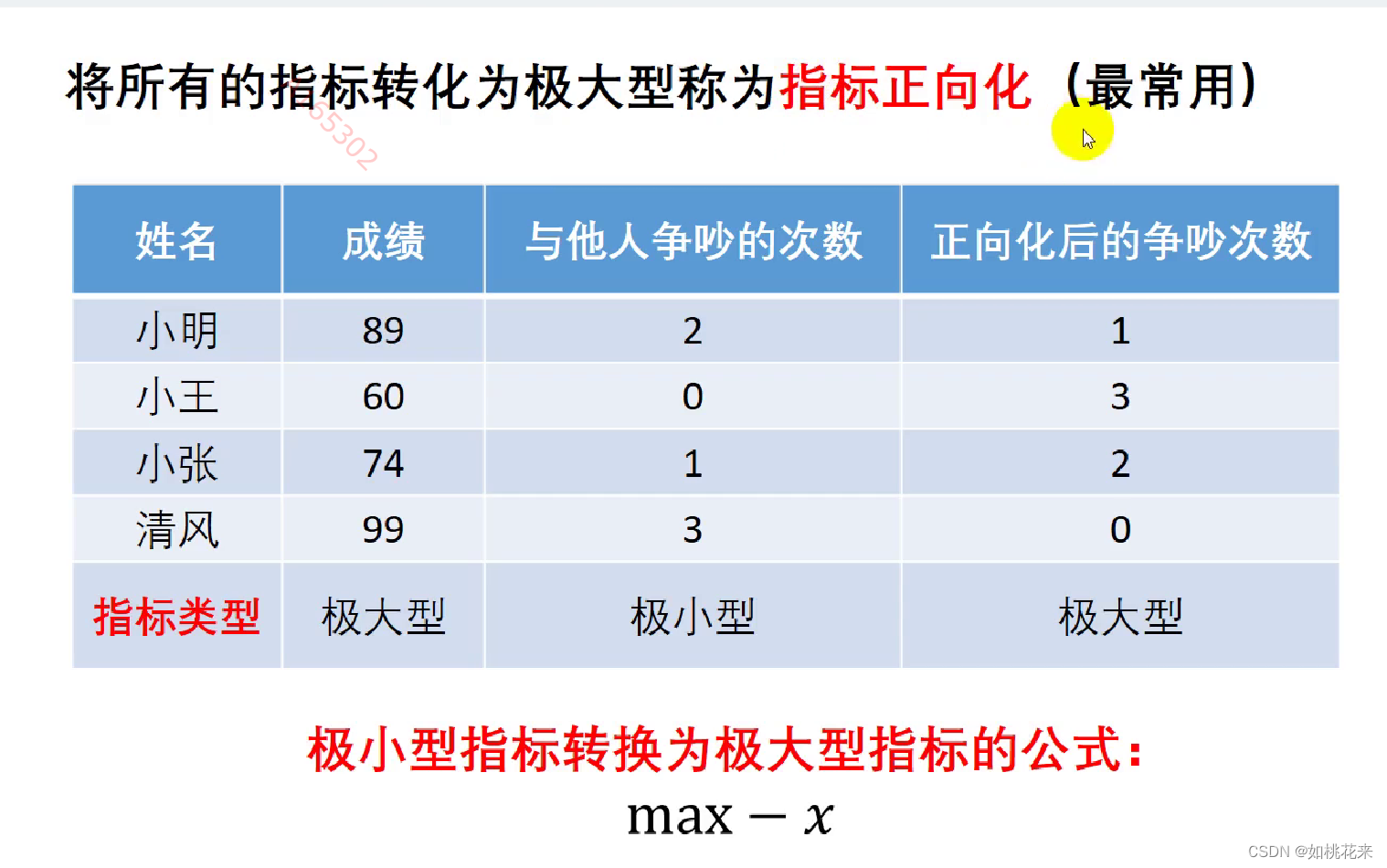
当然了，若是所有元素均为正数，那么也可以使用1/x。但还是推荐第一种max-x

中间型指标正向化公式：

区间型指标正向化公式：

标准化处理(消去单位)：

为了消去不同指标量纲的影响(比如上一题一个单位是分，一个单位是次数)，我们需要对已经正向化的矩阵进行标准化处理。

1. 当前列每一个元素取平方(取平方是因为避免元素产生负数的影响)
2. 对取平方后的列元素求和，再开根号
3. 用当前元素除以2值就是标准化后的结果
4. 标准化后的数值不改变相对大小

代码解析：

%正向化矩阵
X = [89 1;60 3;74 2;99 0];
%对矩阵的行和列进行拆包,n为行,m为列
[n,m] = size(X);
%标准化处理,repmat函数可以将矩阵视为一个整体。按几行几列复制。
res = X./repmat(sum(X.^2).^0.5,n,1)

计算得分：

标准化后的数据还需要计算各指标的总得分，这里不区分权重，所以各项系数均为1

过程解析：

求出z与最大值的距离，最小值同理

1. 求出每个指标下最大的元素，并将它构成行向量
2. 用z的每个指标数据减去1所得的行向量，取平方，再求和。
3. 开根号

代码解析：

clear
clc
%运行标准化结果的文件
run("biao_zhun_hua.m");
[n,m] = size(res);
%求最大距离
max_res = sum((repmat(max(res),n,1)-res).^2,2).^0.5;
%求最小距离
min_res = sum((repmat(min(res),n,1)-res).^2,2).^0.5;
%未归一化后的得分
final_res = min_res./(max_res + min_res);
%归一化后的得分
answer = final_res./repmat(sum(final_res),n,1)

特别注意，这里sum的求和要行求和，因为是各个指标的相加。最后得到的结果是一个列向量，每一列对应一个人的综合得分最大值或者最小值。