AVL树的讲解

算法拾遗三十八AVL树

- - AVL树
  - - AVL树平衡性
    - AVL树加入节点
    - AVL删除节点
    - AVL树代码

AVL树

AVL树具有最严苛的平衡性，（增、删、改、查）时间复杂度为O（logN），AVL树任何一个节点，左树的高度和右树的高度差不超过1（<2）
和SB树，红黑树时间复杂度一样，只是不同的人搞出了不同的平衡性。
AVL树就是一颗搜索二叉树和搜索二叉树的区别主要是做完属于搜索二叉树的调整之后有专属于自己平衡性的补丁。
搜索二叉树加节点，则小于根节点的挂左边，大于根节点的挂右边
搜索二叉树删除节点分情况：
1、当找到了要删除的节点X之后，X既没有左子树也没有右子树，则直接删除
2、找到了要删除的节点X之后，X有左但无右，那么直接让这个删除节点的X的左子树完全替代X
3、如果要删除的节点X，X无左有右，那么直接让右子树替代X
4、如果要删除的X既有左又有右，可以找左树的最右节点（最大节点）或者右树的最左节点（最小节点）代替X

AVL树平衡性

破坏平衡性操作：
LL：
在这里插入图片描述
需要调整为如下：

LR：

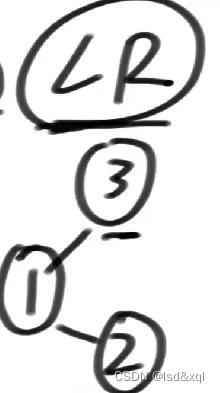
同理还有RR和RL型违规破坏平衡性。

如下图（LR型违规：只要是LR型违规。则让那个孙节点跑上去保持平衡）：
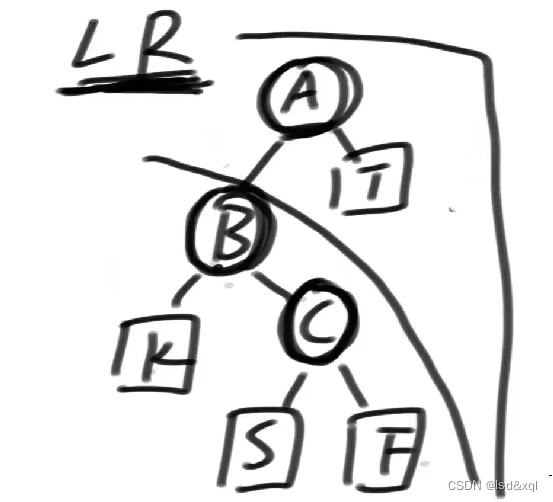
在这里插入图片描述
可知树的不平衡原因为：B的右子树导致的整棵树不平衡，则需要让C来到A节点的位置，那么需要在BC这棵树上对B来一个左旋，得到下图结果：

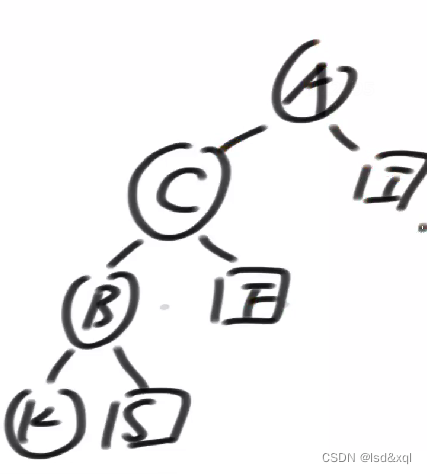
然后再对A来一个右旋C就上去了：

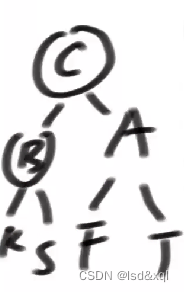
RL型违规：

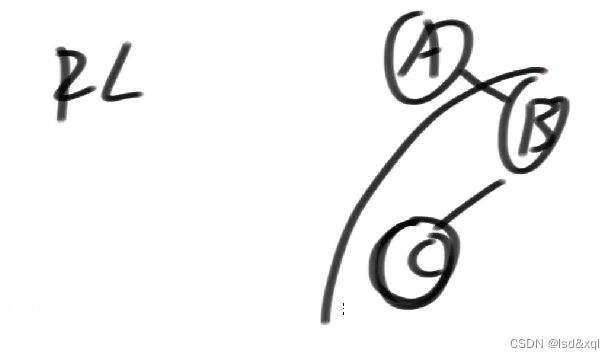
则让它的孙子节点顶上来就完事了，先在B上面执行一个右旋，让C顶上来，再在整棵树上执行一个A的左旋那么最后的C就上来了。

有一个细节：
有没有可能既是LL型违规又是LR型违规：
一棵树的左子树对应的左子树高度和这棵树的右子树对应的右子树高度一样所造成的不平衡是LL和LR型违规
在这里插入图片描述
如上图假设平衡二叉树左树高度为7右树高度为6，在某个时间右树删除一个数导致右树高度为5了，B的左树和右树高度都是6，我的失误既来自LL型又来自LR型

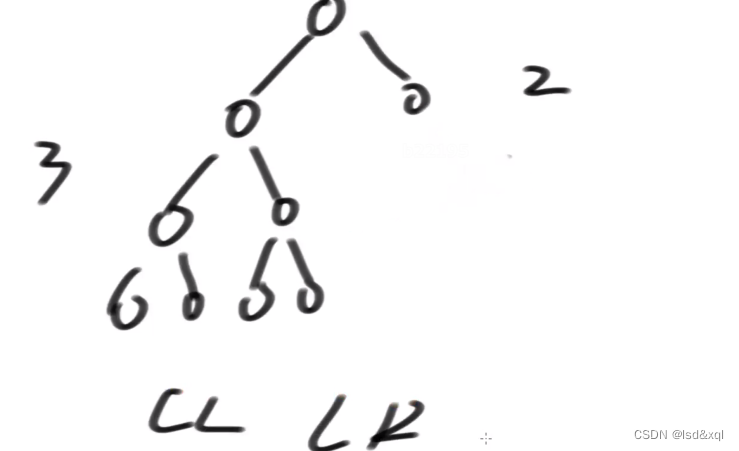
此时一定要按照LL型来调整，直接右旋(总能保证有效)。

如果用LR的方式来调整，则可能不对：有如下图
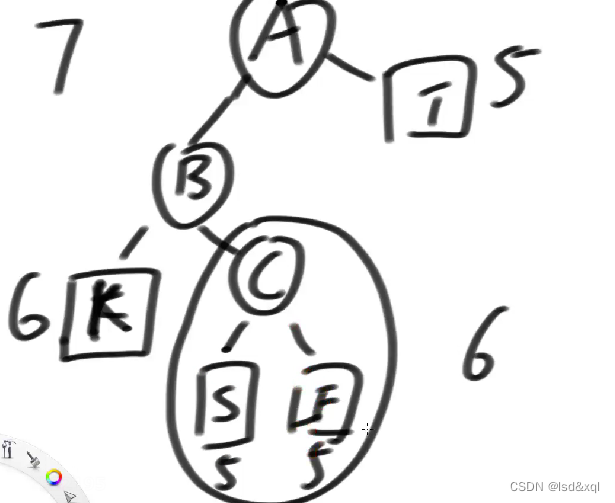
在这里插入图片描述
A的左树高度是7A的右树高度为5，如果这个例子按照LL型调整：会发现这棵树的高度是异常平衡的

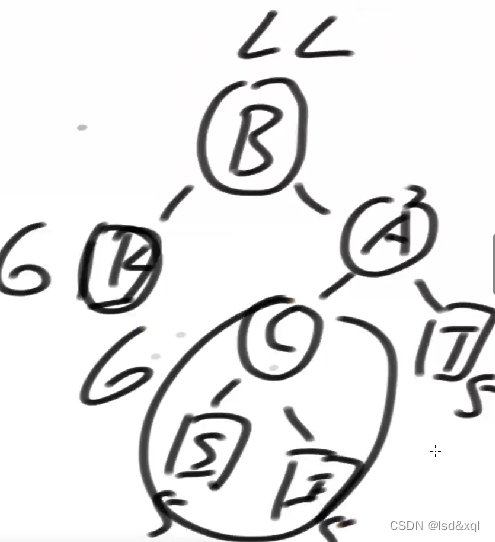
如果按照LR方式来调整：如果将S的高度调整成4的话
这样调整出来的K，S则不平了

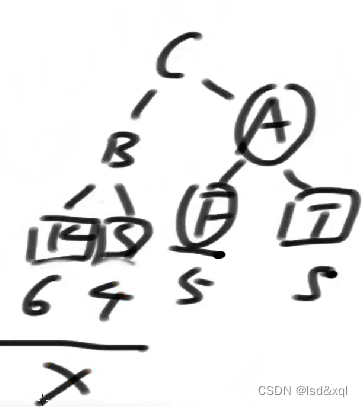
再来一个不平衡的：

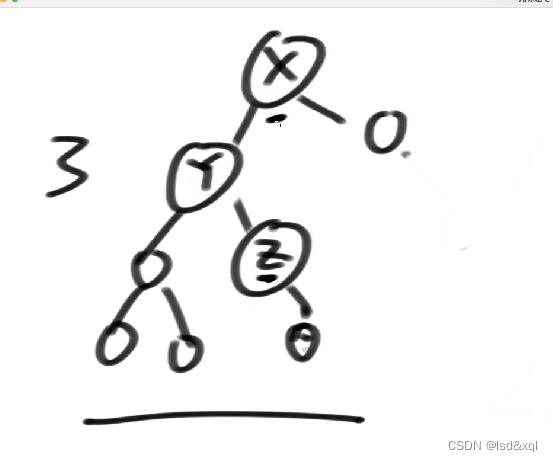
按照LR方式进行调整，z替代y的位置
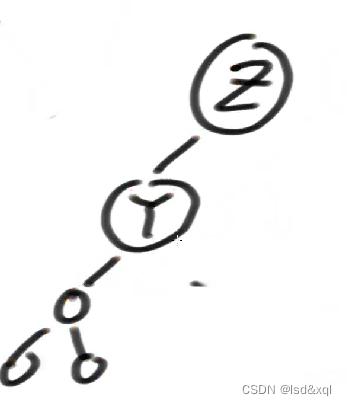
在这里插入图片描述
y接受了z的左空子树，y的右边是没有东西的，最后调整成这样：

综上：
总结：LL型违规只用进行一次右旋，LR型违规则需要进行一次小范围的左旋，再执行整棵树的右旋，RL型违规则需要先进行小范围上的右旋，再进行整棵树的左旋，RR型只需要进行一次左旋，时间复杂度均为O（1）

AVL树加入节点

加入一个节点之后需要依次查询加入的节点中了哪种类型的违规，如果未找到违规则找其对应的父节点，如果父节点未违规则继续找父节点对应的父节点，一直找到根节点未违规为止。
所以AVL树调整不是只对一个节点查是沿途所有节点都需要查（防止旋转一次后其上的节点还需要旋转），整体时间复杂度为O（logN）的调整代价，

如下图加入一个节点X首先看当前X节点是平的，再看X对应的父节点也是平的，最终找到方框标记的节点发现不再平衡了，左树高度为1，右树高度为3，而且是RR型违规
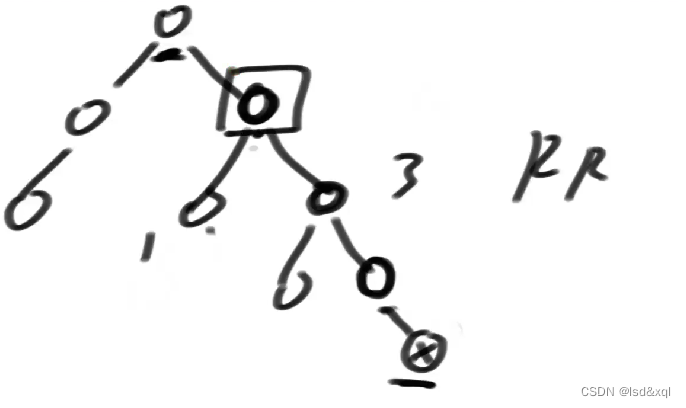
在这里插入图片描述
则需要进行左旋

AVL删除节点

分为以下情况：
1、X节点既没有左也没有右子树，这种情况只需要从删除节点开始算上面每一个父都要全查一遍。
2、X节点有右无左，直接拿右孩子替换原来的X，然后从右孩子来到的位置往上查询一遍
3、X节点既有左又有右孩子，看如下例子
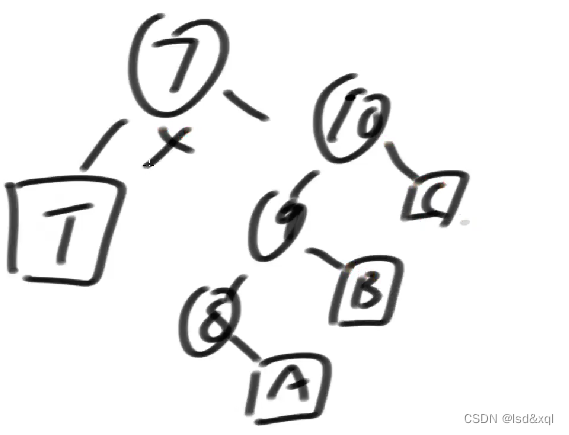
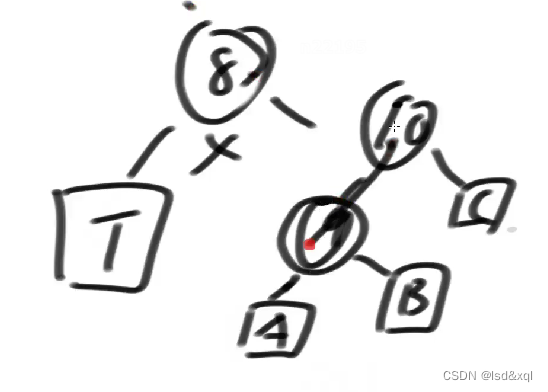
在这里插入图片描述
如果此处要删掉7，则需要找到7对应右孩子的最小值8去替换7的位置，调整成如下图的样子，此时只需要从9开始查它的父节点依次调整即可，

AVL树代码

右旋步骤：
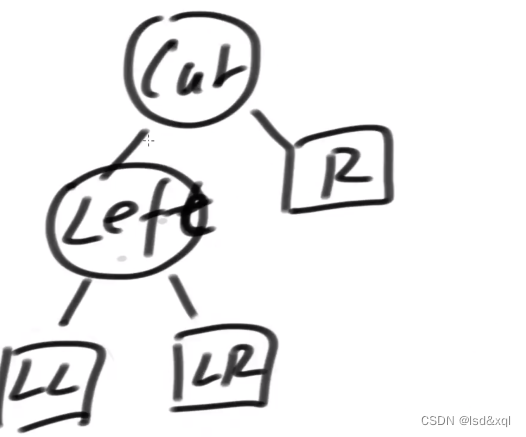
在这里插入图片描述

1、当前树的左边去接管左孩子的右
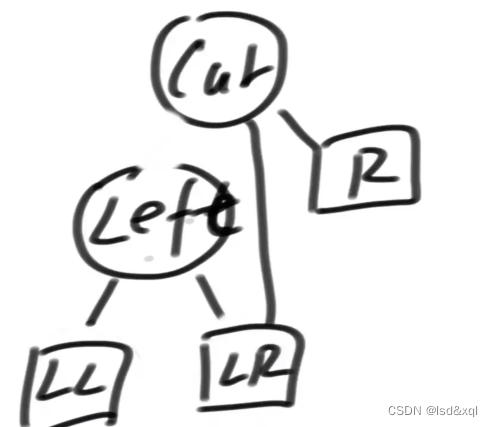
在这里插入图片描述
2、左孩子的右会接管cur

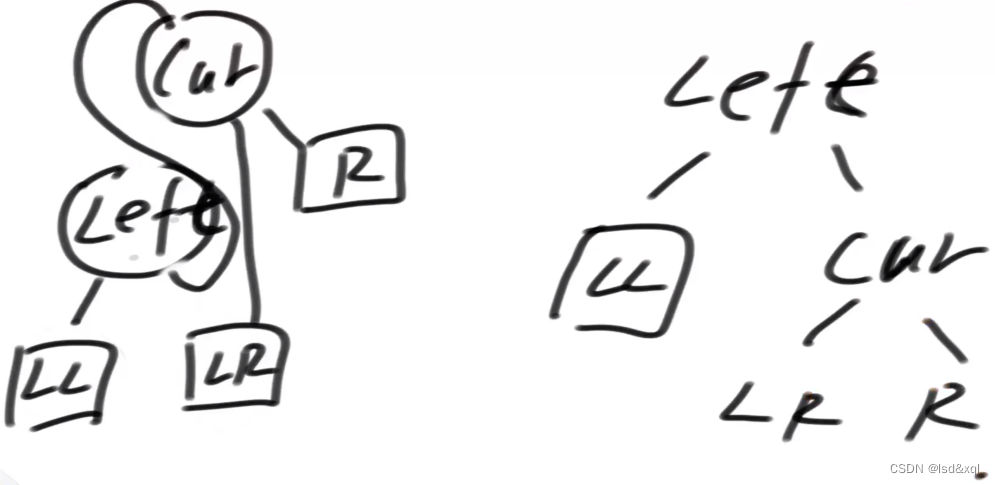
参照代码：

	//右旋private AVLNode<K, V> rightRotate(AVLNode<K, V> cur) {//记录左孩子AVLNode<K, V> left = cur.l;//左孩子的右树挂载当前树的左边cur.l = left.r;//左孩子的右接管curleft.r = cur;//高度也得接管（现在左孩子和右孩子的高度最大的那个再加1）cur.h = Math.max((cur.l != null ? cur.l.h : 0), (cur.r != null ? cur.r.h : 0)) + 1;left.h = Math.max((left.l != null ? left.l.h : 0), (left.r != null ? left.r.h : 0)) + 1;//右旋以left做头节点返回return left;}

再看AVL树add节点：
当前来到cur节点，要加的key是啥要加的value是啥，搜索二叉树潜台词为加入的key都不一样

public class Code_AVLTreeMap {public static class AVLNode<K extends Comparable<K>, V> {public K k;public V v;//左孩子及右孩子public AVLNode<K, V> l;public AVLNode<K, V> r;//高度public int h;public AVLNode(K key, V value) {k = key;v = value;h = 1;}}public static class AVLTreeMap<K extends Comparable<K>, V> {//根节点private AVLNode<K, V> root;//一共加入多少个节点private int size;public AVLTreeMap() {root = null;size = 0;}//右旋private AVLNode<K, V> rightRotate(AVLNode<K, V> cur) {//记录左孩子AVLNode<K, V> left = cur.l;//左孩子的右树挂载当前树的左边cur.l = left.r;//左孩子的右接管curleft.r = cur;//高度也得接管（现在左孩子和右孩子的高度最大的那个再加1）cur.h = Math.max((cur.l != null ? cur.l.h : 0), (cur.r != null ? cur.r.h : 0)) + 1;left.h = Math.max((left.l != null ? left.l.h : 0), (left.r != null ? left.r.h : 0)) + 1;//右旋以left做头节点返回return left;}//左旋private AVLNode<K, V> leftRotate(AVLNode<K, V> cur) {AVLNode<K, V> right = cur.r;cur.r = right.l;right.l = cur;cur.h = Math.max((cur.l != null ? cur.l.h : 0), (cur.r != null ? cur.r.h : 0)) + 1;right.h = Math.max((right.l != null ? right.l.h : 0), (right.r != null ? right.r.h : 0)) + 1;return right;}//平衡性调整private AVLNode<K, V> maintain(AVLNode<K, V> cur) {if (cur == null) {return null;}int leftHeight = cur.l != null ? cur.l.h : 0;int rightHeight = cur.r != null ? cur.r.h : 0;//此时左右树高度差大于1不平衡了if (Math.abs(leftHeight - rightHeight) > 1) {//左树高还是右树高if (leftHeight > rightHeight) {//左树高int leftLeftHeight = cur.l != null && cur.l.l != null ? cur.l.l.h : 0;int leftRightHeight = cur.l != null && cur.l.r != null ? cur.l.r.h : 0;//左树的左树高度大于等于右树的右树高度则LL型if (leftLeftHeight >= leftRightHeight) {//LL型违规cur = rightRotate(cur);} else {//LR型违规cur.l = leftRotate(cur.l);cur = rightRotate(cur);}} else {int rightLeftHeight = cur.r != null && cur.r.l != null ? cur.r.l.h : 0;int rightRightHeight = cur.r != null && cur.r.r != null ? cur.r.r.h : 0;if (rightRightHeight >= rightLeftHeight) {//RRcur = leftRotate(cur);} else {//RLcur.r = rightRotate(cur.r);cur = leftRotate(cur);}}}return cur;}private AVLNode<K, V> findLastIndex(K key) {AVLNode<K, V> pre = root;AVLNode<K, V> cur = root;while (cur != null) {pre = cur;if (key.compareTo(cur.k) == 0) {break;} else if (key.compareTo(cur.k) < 0) {cur = cur.l;} else {cur = cur.r;}}return pre;}private AVLNode<K, V> findLastNoSmallIndex(K key) {AVLNode<K, V> ans = null;AVLNode<K, V> cur = root;while (cur != null) {if (key.compareTo(cur.k) == 0) {ans = cur;break;} else if (key.compareTo(cur.k) < 0) {ans = cur;cur = cur.l;} else {cur = cur.r;}}return ans;}private AVLNode<K, V> findLastNoBigIndex(K key) {AVLNode<K, V> ans = null;AVLNode<K, V> cur = root;while (cur != null) {if (key.compareTo(cur.k) == 0) {ans = cur;break;} else if (key.compareTo(cur.k) < 0) {cur = cur.l;} else {ans = cur;cur = cur.r;}}return ans;}//AVL树加节点private AVLNode<K, V> add(AVLNode<K, V> cur, K key, V value) {if (cur == null) {//如果当前树为null，则新建节点return new AVLNode<K, V>(key, value);} else {//如果key小于当前树的kif (key.compareTo(cur.k) < 0) {//我去左树上面找，头部调整为当前节点的左树//之所以用cur.l = xxx 是因为这条记录挂在左树上是可能换头的//需要将返回值由我的头指针的左子树重新指一下接住cur.l = add(cur.l, key, value);} else {//右树上挂cur.r = add(cur.r, key, value);}//我自己的高度调整对cur.h = Math.max(cur.l != null ? cur.l.h : 0, cur.r != null ? cur.r.h : 0) + 1;//做平衡调整return maintain(cur);}}// 在cur这棵树上，删掉key所代表的节点// 返回cur这棵树的新头部private AVLNode<K, V> delete(AVLNode<K, V> cur, K key) {if (key.compareTo(cur.k) > 0) {cur.r = delete(cur.r, key);} else if (key.compareTo(cur.k) < 0) {cur.l = delete(cur.l, key);} else {if (cur.l == null && cur.r == null) {cur = null;} else if (cur.l == null && cur.r != null) {cur = cur.r;} else if (cur.l != null && cur.r == null) {cur = cur.l;} else {AVLNode<K, V> des = cur.r;while (des.l != null) {des = des.l;}//调用右树删除整个k，同时调整了平衡cur.r = delete(cur.r, des.k);des.l = cur.l;des.r = cur.r;cur = des;}}if (cur != null) {cur.h = Math.max(cur.l != null ? cur.l.h : 0, cur.r != null ? cur.r.h : 0) + 1;}return maintain(cur);}public int size() {return size;}public boolean containsKey(K key) {if (key == null) {return false;}AVLNode<K, V> lastNode = findLastIndex(key);return lastNode != null && key.compareTo(lastNode.k) == 0 ? true : false;}public void put(K key, V value) {if (key == null) {return;}AVLNode<K, V> lastNode = findLastIndex(key);if (lastNode != null && key.compareTo(lastNode.k) == 0) {lastNode.v = value;} else {size++;root = add(root, key, value);}}public void remove(K key) {if (key == null) {return;}if (containsKey(key)) {size--;root = delete(root, key);}}public V get(K key) {if (key == null) {return null;}AVLNode<K, V> lastNode = findLastIndex(key);if (lastNode != null && key.compareTo(lastNode.k) == 0) {return lastNode.v;}return null;}public K firstKey() {if (root == null) {return null;}AVLNode<K, V> cur = root;while (cur.l != null) {cur = cur.l;}return cur.k;}public K lastKey() {if (root == null) {return null;}AVLNode<K, V> cur = root;while (cur.r != null) {cur = cur.r;}return cur.k;}public K floorKey(K key) {if (key == null) {return null;}AVLNode<K, V> lastNoBigNode = findLastNoBigIndex(key);return lastNoBigNode == null ? null : lastNoBigNode.k;}public K ceilingKey(K key) {if (key == null) {return null;}AVLNode<K, V> lastNoSmallNode = findLastNoSmallIndex(key);return lastNoSmallNode == null ? null : lastNoSmallNode.k;}}}