LeetCode 1162. As Far from Land as Possible【多源BFS】中等

本文属于「征服LeetCode」系列文章之一，这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁，本系列将至少持续到刷完所有无锁题之日为止；由于LeetCode还在不断地创建新题，本系列的终止日期可能是永远。在这一系列刷题文章中，我不仅会讲解多种解题思路及其优化，还会用多种编程语言实现题解，涉及到通用解法时更将归纳总结出相应的算法模板。

为了方便在PC上运行调试、分享代码文件，我还建立了相关的仓库：https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中，你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等，还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解，还可以一同分享给他人。

由于本系列文章的内容随时可能发生更新变动，欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。

你现在手里有一份大小为 n x n 的网格 grid，上面的每个单元格都用 0 和 1 标记好了。其中 0 代表海洋，1 代表陆地。

请你找出一个海洋单元格，这个海洋单元格到离它最近的陆地单元格的距离是最大的，并返回该距离。如果网格上只有陆地或者海洋，请返回 -1。

我们这里说的距离是「曼哈顿距离」（ Manhattan Distance）：(x0, y0) 和 (x1, y1) 这两个单元格之间的距离是 |x0 - x1| + |y0 - y1| 。

示例 1：

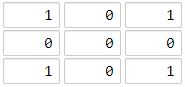
输入：grid = [[1,0,1],[0,0,0],[1,0,1]]
输出：2
解释： 
海洋单元格 (1, 1) 和所有陆地单元格之间的距离都达到最大，最大距离为 2。

示例 2：

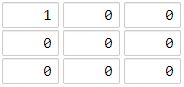
输入：grid = [[1,0,0],[0,0,0],[0,0,0]]
输出：4
解释：
海洋单元格 (2, 2) 和所有陆地单元格之间的距离都达到最大，最大距离为 4。

提示：

n == grid.length
n == grid[i].length
1 <= n <= 100
grid[i][j] 不是 0 就是 1

本题与542. 01 Matrix相同。

解法多源BFS

这里不是求某一个海洋区域到陆地区域的最短路，而是求所有的海洋区域到陆地区域这个「点集」的最短路。显然这不是一个「单源」最短路问题（SSSP）。在我们学习过的最短路算法中，求解 SSSP 问题的方法有 Dijkstra 算法和 SPFA算法，而求解任意两点之间的最短路一般使用 Floyd 算法。那我们在这里就应该使用 Floyd 算法吗？

要考虑这个问题，我们需要分析一下这里使用 Floyd 算法的时间复杂度。我们知道在网格图中求最短路，每个区域（格子）相当于图中的顶点，而每个格子和上下左右四个格子的相邻关系相当于边，我们记顶点的个数为 $V$ ，Floyd 算法的时间复杂度为 $O(V^3)$ ，而这里 $V = n^2$ ，所以 $O(V^3) = O(n^6)$ ，显然是不现实的。

考虑 SSSP 是求一个源点到一个点集中所有点的最短路，而这个问题的本质是求某个点集到另一个点集中所有点的最短路，即「多源最短路」，我们只需要对 Dijkstra 算法或者 SPFA 算法稍作修改。这里以 Dijkstra 算法为例，我们知道堆优化的 Dijkstra 算法实际上是 BFS 的一个变形，把 BFS 中的队列变成了优先队列，在拓展新状态的时候加入了松弛操作。Dijkstra 的堆优化版本第一步是源点入队，我们只需要把它改成源点集合中的所有的点入队，就可以实现求「多源最短路」。

思考：为什么？
因为我们这样做相当于建立了一个超级源点 $S$ ，这个点与源点集中的 $s_0, s_1, s_2 \cdots s_{|V|}$ 都有边，并且权都为 $0$ 。这样求源点集到目标点集的最短路，就变成了求超级源点 $S$ 到它们的最短路，于是又转化成了 SSSP 问题。

继续思考：海洋区域和陆地区域，应该哪一个作为源点集？
也许你分析出「我们需要找一个海洋区域，满足它到陆地的最小距离是最大」会把海洋区域作为源点集。考虑后续的实现，我们知道 Dijkstra 中一个 $d$ 数组用来维护当前源点集到其他点的最短路，而对于源点集中的任意一个点 $s$ ， $d[s_x][s_y] = 0$ ，这很好理解，源点到源点的最短路就是 $0$ 。如果我们把海洋区域作为源点集、陆地区域作为目标点集，假设 $t$ 是目标点集中的一个点，算法执行结束后 $d[t_x][t_y]$ 就是海洋区域中的点到 $t$ 的最短距离，但是我们却不知道哪些 $t$ 是海洋区域点的「最近陆地区域」，我们也不知道每个 $s$ 距离它的「最近陆地区域」的曼哈顿距离。

考虑我们把陆地区域作为源点集、海洋区域作为目标点集，目标点集中的点 $t$ 对应的 $d[t_x][t_y]$ 就是海洋区域 $t$ 对应的距离它的「最近陆地区域」的曼哈顿距离，正是我们需要的，所以应该把陆地区域作为源点集。最终只需要比出 $d[t_x][t_y]$ 的最大值即可。如果使用 Dijkstra 算法，那么在初始化 d 数组时，把每个元素预置为 INF，所以如果发现最终比出的最大值为 INF，那么就返回 $- 1$ 。

由于这里的边权为 $1$ ，不如直接使用多源 BFS，在这里每个点都只会被松弛一次。

class Solution {
public:int maxDistance(vector<vector<int>>& grid) {int n = grid.size();queue<pair<int, int>> q;int MAX_VALUE = n + n;for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {if (grid[i][j] == 1) {grid[i][j] = 0;q.push({i, j});} else grid[i][j] = MAX_VALUE;}}int d[4][2] = {-1, 0, 1, 0, 0, -1, 0, 1};int ans = -1;while (!q.empty()) {auto [x, y] = q.front(); q.pop();for (int i = 0; i < 4; ++i) {int u = x + d[i][0], v = y + d[i][1];if (u >= 0 && u < n && v >= 0 && v < n && grid[x][y] + 1 < grid[u][v]) {// 只有海洋单元格的值会被更新,且一次性更新为到最近陆地单元格的距离grid[u][v] = grid[x][y] + 1;ans = max(ans, grid[u][v]);q.push({u, v});}}}return ans;}
};