目录

GAN：对抗生成网络

损失函数

判别器开始波动很大，先调整判别器

 生成样本和真实样本的统一：真假难辨​编辑

 文字专图片​编辑

 头像转表情包​编辑

 头像转3D​编辑

后向传播

1. 前向传播（forward）

2. 反向传播（backward）：得到权重参数公式，寻找优路径

反向传播的四个基本方程

链式法则误差求和

 梯度下降权重参数更新​编辑

---

GAN：对抗生成网络

 

 

 

损失函数

 

判别器开始波动很大，先调整判别器

 生成样本和真实样本的统一：真假难辨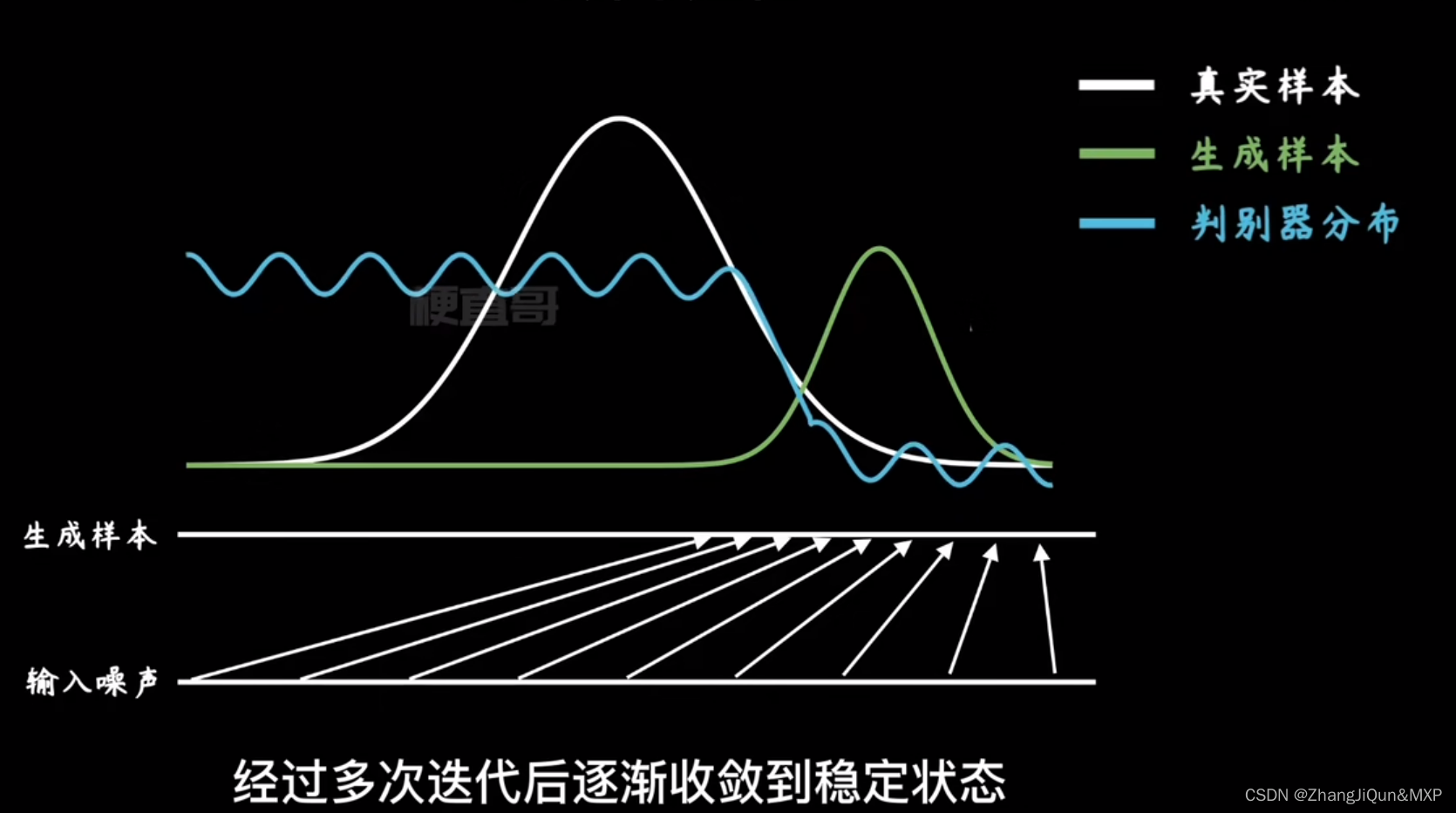

 

 

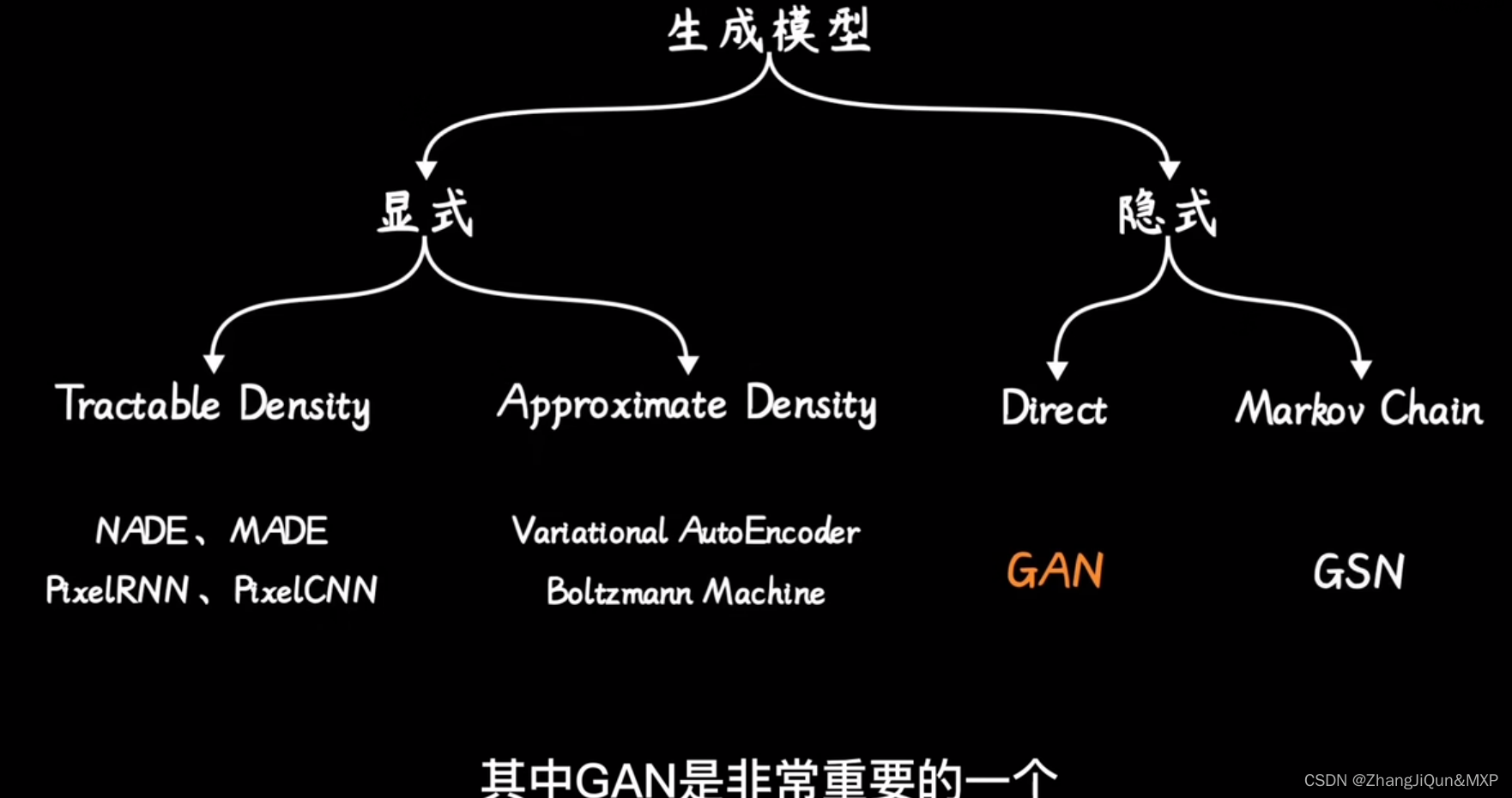
 图像数据集生成

 

 文字专图片

 头像转表情包

 头像转3D

 贝叶斯：后验

 

 

 

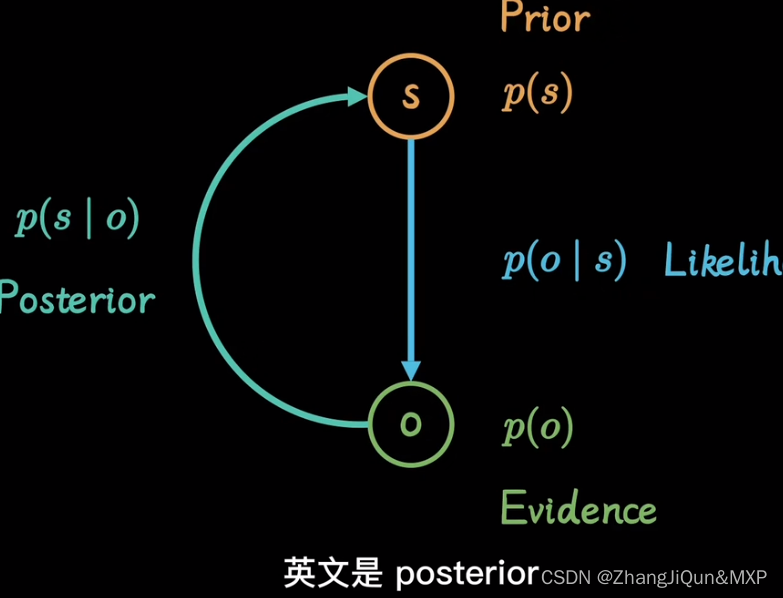
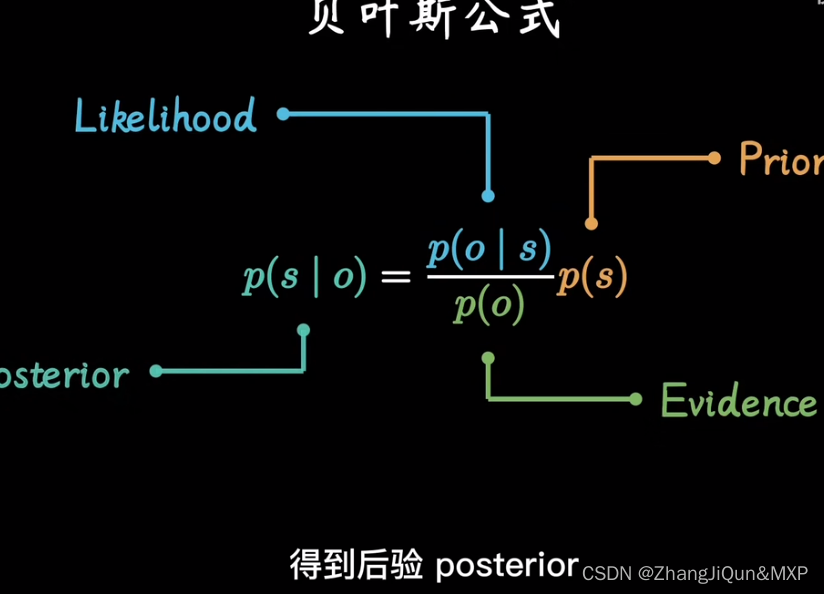
后向传播

 

 

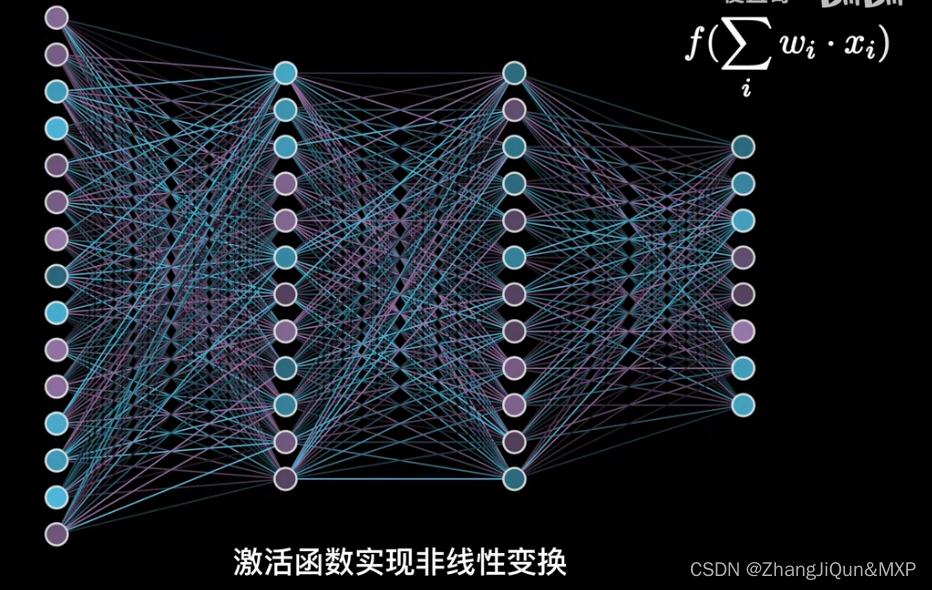
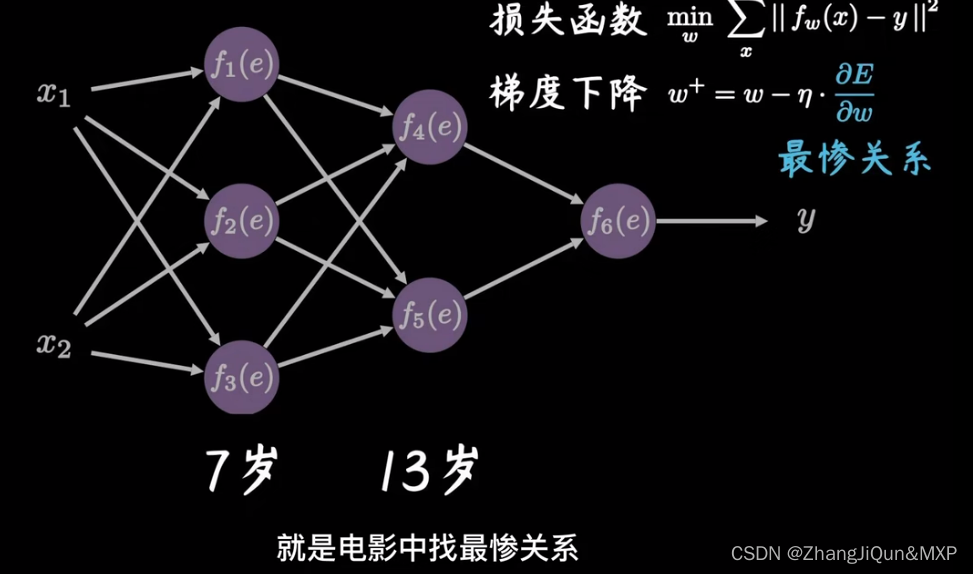
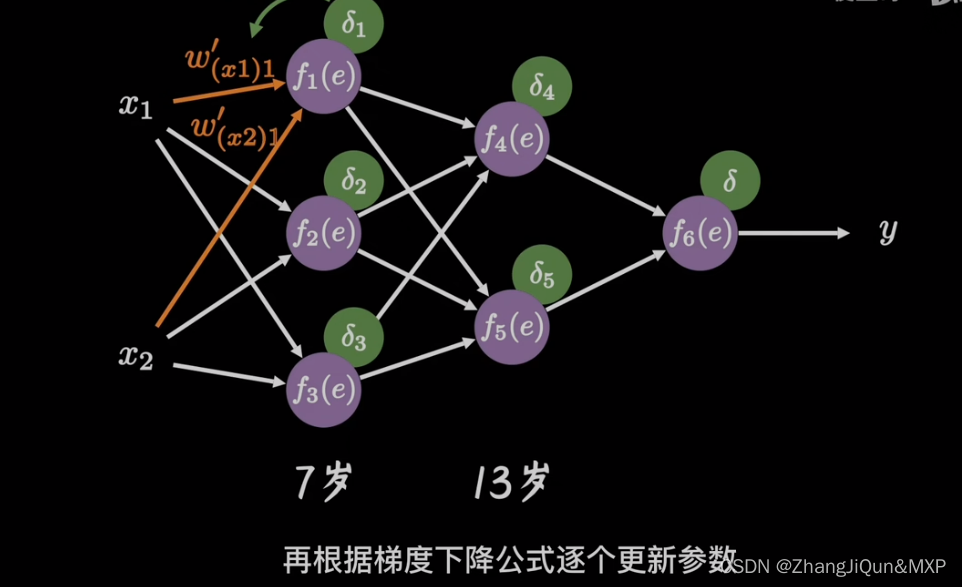
前向传播：通过输入层输入，一路向前，通过输出层输出的一个结果。如图指的是1 、 x1、x2、xn、与权重（weights）相乘，并且加上偏置值b0，然后进行总的求和，同时通过激活函数激活之后算出结果。这个过程就是前向传播。
反向传播：通过输出反向更新权重的过程。具体的说输出位置会产生一个模型的输出，通过这个输出以及原数据计算一个差值。将前向计算过程反过来计算。通过差值和学习率更新权重。

1. 前向传播（forward）

简单理解就是将上一层的输出作为下一层的输入，并计算下一层的输出，一直到运算到输出层为止。接下来我们用数学公式描述一下：

权重

偏置

设 wjkl 为 l−1 层第 k 个神经元到第 l 层第 j 个神经元的weight， bjl 为第 l 层第 j 个神经元的bias， ajl 为第第 l 层第 j 个神经元的激活值（激活函数的输出，保证模型的非线性）。

对于Layer 2的输出 a1(2) ，a2(2)，a3(2)，

a1(2)=σ(z1(2))=σ(w11(2)x1+w12(2)x2+w13(2)x3+b1(2))

a2(2)=σ(z2(2))=σ(w21(2)x1+w22(2)x2+w23(2)x3+b2(2))

a3(2)=σ(z3(2))=σ(w31(2)x1+w32(2)x2+w33(2)x3+b3(2))

对于Layer 3的输出a1(3)，

a1(3)=σ(z1(3))=σ(w11(3)a1(2)+w12(3)a2(2)+w13(3)a3(2)+b1(3))

a2(3)=σ(z2(3))=σ(w21(3)a1(2)+w22(3)a2(2)+w23(3)a3(2)+b2(3))

从上面可以看出，使用代数法一个个的表示输出比较复杂，而如果使用矩阵法则比较的简洁。将上面的例子一般化，并写成矩阵乘法的形式，

z(l)=W(l)a(l−1)+b(l)

a(l)=σ(z(l))

其中 σ 为 激活函数，如Sigmoid，ReLU，PReLU等。

2. 反向传播（backward）：得到权重参数公式，寻找优路径

实际上，反向传播仅指用于计算梯度的方法。而另一种算法，例如随机梯度下降法，才是使用该梯度来进行学习。原则上反向传播可以计算任何函数的到导数。

在了解反向传播算法之前，我们先简单介绍一下链式法则：

微积分中的链式法则（为了不与概率中的链式法则相混淆）用于计复合函数的导数。反向传播是一种计算链式法则的算法，使用高效的特定运输顺序。

设 x 是实数， f 和 g 是从实数映射到实数的函数。假设 y=g(x) 并且 z=f(g(x))=f(y) 。那么链式法则就是： dzdx=dzdydydx 。

反向传播算法的核心是代价函数 C 对网络中参数（各层的权重 W 和偏置 b ）的偏导表达式 ∂C∂W 和∂C∂b。这些表达式描述了代价函数值C随权重W或偏置b变化而变化的程度。BP算法的简单理解：如果当前代价函数值距离预期值较远，那么我们通过调整权重W或偏置b的值使新的代价函数值更接近预期值（和预期值相差越大，则权重W或偏置b调整的幅度就越大）。一直重复该过程，直到最终的代价函数值在误差范围内，则算法停止。

BP算法可以告诉我们神经网络在每次迭代中，网络的参数是如何变化的，理解这个过程对于我们分析网络性能或优化过程是非常有帮助的，所以还是尽可能搞透这个点。

反向传播过程中要计算偏导表达式 ∂C/∂W 和∂C/∂b，我们先对代价函数做两个假设，以二次损失函数为例：

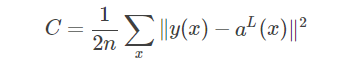
其中 n 为训练样本 x 的总数， y=y(x) 为期望的输出，即ground truth， L 为网络的层数， aL(x) 为网络的输出向量。

假设1：总的代价函数可以表示为单个样本的代价函数之和的平均：

　这个假设的意义在于，因为反向传播过程中我们只能计算单个训练样本的∂Cx/∂Wx 和∂C/∂b，在这个假设下，我们可以通过计算所有样本的平均来得到总体的∂C/∂W 和∂C/∂b。

假设2：代价函数可以表达为网络输出的函数 Loss=C(aL) ，比如单个样本 x 的二次代价函数可以写为：

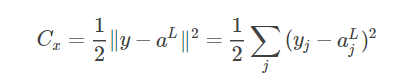
反向传播的四个基本方程

权重W或偏置b的改变如何影响代价函数 C 是理解反向传播的关键。最终，这意味着我们需要计算出每个的∂C/∂Wjkl 和∂C/∂bjkl，在讨论基本方程之前，我们引入误差 δ 的概念，δjl表示第 l 层第 j 个神经元的误差。

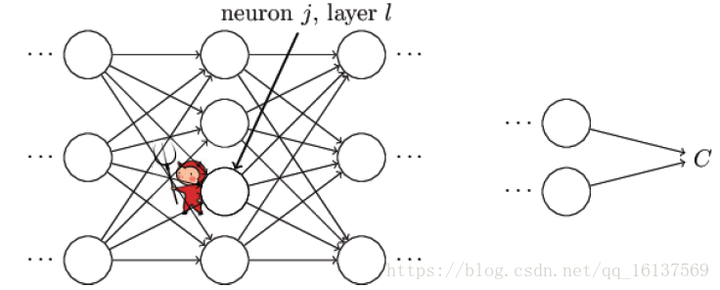
如上图所示，假设有个小恶魔在第 l 层第 j 个神经元捣蛋，他让这个神经元的权重输出变化了 Δzjl ，那么这个神经元的激活输出为 δ(zjl+Δzjl) ，然后这个误差向后逐层传播下去，导致最终的代价函数变化了 ∂C/∂zjlΔzjl 。现在这个小恶魔改过自新，它想帮助我们尽可能减小代价函数的值（使网络输出更符合预期）。假设 ∂C∂zjl 一开始是个很大的正值或者负值，小恶魔通过选择一个和 ∂C/∂zjl 方向相反的Δzjl使代价函数更小（这就是我们熟知的梯度下降法）。随着迭代的进行， ∂C/∂zjl 会逐渐趋向于0，那么Δzjl对于代价函数的改进效果就微乎其微了，这时小恶魔就一脸骄傲的告诉你：“俺已经找到了最优解了（局部最优）”。这启发我们可以用 ∂C/∂zjl 来衡量神经元的误差： δjl=∂C∂zjl 。

下面就来看看四个基本方程是怎么来的。

1. 输出层的误差方程

果上面的东西你看明白了，这个方程应该不难理解，等式右边第一项 ∂C∂ajL 衡量了代价函数随网络最终输出的变化快慢，而第二项 σ(1)(zjL) 则衡量了激活函数输出随 zjL 的变化快慢。当激活函数饱和，即 σ(1)(zjL)≈0 时,无论∂C∂ajL多大，最终 δjL≈0 ，输出神经元进入饱和区，停止学习。

方程中两项都很容易计算，如果代价函数为二次代价函数：

可以得到：

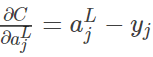
同理，对激活函数 σ(z) 求 zjL 的偏导即可求得 σ(1)(zjL) ,将它重写为矩阵形式：

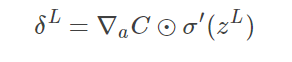
⊙ 为Hadamard积，即矩阵的点积。

链式法则误差求和

 梯度下降权重参数更新