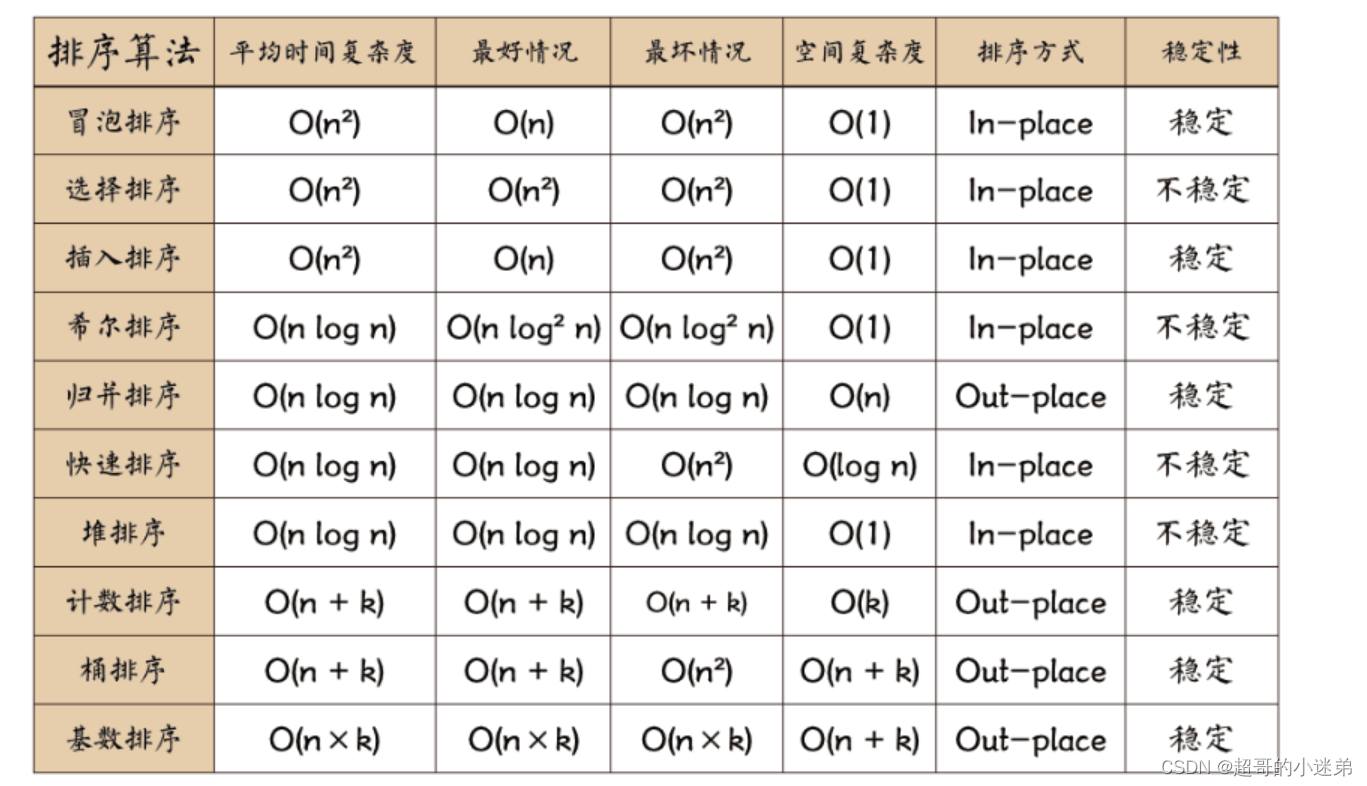
1、排序算法
1.1、堆排序(大顶堆)-重点:
-
参考文章:堆排序1、堆排序二
-
前置知识:
- 大顶堆:完全二叉树,且父节点大于左右儿子,左右子树又是大顶堆,依赖数组来实现(vector)
- 第一个节点的父节点:
(i-1)/2,第i个节点的左儿子:i*2+1,第i个节点的右儿子:i*2+2,这里i从0开始; - 最后有儿子的节点:数组元素有
n个,则最后一个有儿子的节点(n-1-1)/2=n/2-1
-
堆排序基本思想:分为
建堆和排序两步,而核心步骤是对堆的属性进行维护- 维护堆:维护第i个节点的堆属性, 将该节点和左右儿子节点进行对比,选择大的进行交换,然后向下遍历,直到全部都满足堆的属性
- 建堆:对已有的数组,从最后一个有儿子的节点开始向上遍历建立大顶堆,每次都需要维护节点的堆属性
- 排序:每次将第一个元素和最后一个元素进行交换,每次交换,需要维护的数组长度-1,维护的节点是第一个节点
-
复杂度:
- 时间复杂度:最坏、最好、平均时间复杂度均为
O(nlogn) - 空间复杂度:
O(1) - 描述:是个不稳定的内部排序算法
- 时间复杂度:最坏、最好、平均时间复杂度均为
-
代码实现:实列测试
class Solution { public:void heapify(vector<int>& nums,int n,int i) //维护第i个节点的堆结构{int largest = i;int left = i*2+1;//最多遍历树的高度,时间复杂度O(log n)while(left<n) //当left是最后一个节点,也还需要判断一次{if(left<n&&nums[largest]<nums[left]) largest = left; if(left+1<n&&nums[largest]<nums[left+1]) largest = left+1; //if(largest==i) break; //当没有子节点的时候,或者不需要维护的时候跳出whileswap(nums[largest],nums[i]); //将大的值放到i的位置上i = largest; //向下循环子节点left = i*2+1; //子节点的左儿子}}void heapSort(vector<int>& nums,int n){//建堆时间复杂度O(nlog n),从第一个有子节点的节点开始维护for(int i =n/2-1;i>=0;i--) {heapify(nums,n,i); }for(int i=n-1;i>=0;i--) //堆排序 时间复杂度O(nlogn){ //每次将最后一个节点和第一个节点互换swap(nums[i],nums[0]);heapify(nums,i,0); //进行枝剪维护第0个节点}}vector<int> sortArray(vector<int>& nums) {heapSort(nums,nums.size());return nums;} };
1.2、快速排序-重点
- 快速排序基本思想:在区间中,每次选择一个基点,小于基点的放在基点左边,大于基点的放在右边,分别对两边进行快速排序
- 复杂度:
- 时间复杂度:最好、平均时间复杂度为
O(nlogn),最坏时间复杂度O(n^2)-序列基本有序,递归O(n)次 - 空间复杂度: 递归深度
O(log n) - 描述:是个不稳定的内部排序
- 时间复杂度:最好、平均时间复杂度为
- 代码实现:参考视频
-
二路快排,普通快排
class Solution { public:int partition(vector<int>& nums,int l,int r){int pivot = rand()%(r-l+1)+l;swap(nums[pivot],nums[r]);int i=l;for(int j=l;j<=r-1;j++) //用j遍历数组,{if(nums[j]<nums[r]){swap(nums[j],nums[i]); //指针i始终指向pivot右边的第一个元素i++; //i前面的都是小于pivot的元素,}}//遍历完了,i依旧指向大于pivot的元素的第一位// j指向r的位置,也就是pivot的位置,只需要将pivot的位置和i的位置进行交换即可swap(nums[r],nums[i]);return i;}void quikSort(vector<int>& nums,int left,int right){if(left>=right) return;int mid = partition(nums,left,right);quikSort(nums,left,mid-1);quikSort(nums,mid+1,right);}vector<int> sortArray(vector<int>& nums) {quikSort(nums,0,nums.size()-1);return nums;} }; -
三路快排,用于重复元素多的情况
class Solution { public:vector<int> partition(vector<int>& nums,int l,int r){int pivot = rand()%(r-l+1)+l;swap(nums[pivot],nums[r]);// 三路快排,p指向pivot元素相同的第一个元素// i指向大于pivot的元素的第一个位置int i=l;int p=l;for(int j=l;j<=r-1;j++){if(nums[j]<nums[r]){swap(nums[j],nums[i]);swap(nums[i],nums[p]);i++; p++;}else if(nums[j]==nums[r]){swap(nums[j],nums[i]);i++;}}swap(nums[r],nums[i]);return vector<int>{p,i};}void quikSort(vector<int>& nums,int left,int right){if(left>=right) return;vector<int> v = partition(nums,left,right);quikSort(nums,left,v[0]-1);quikSort(nums,v[1]+1,right);}vector<int> sortArray(vector<int>& nums) {quikSort(nums,0,nums.size()-1);return nums;} };
-
1.3、归并排序-重点
- 归并排序基本思想:分治的思想,每将数组递归分成长度接近的两个部分,再进行排序合并回溯
- 复杂度:
- 时间复杂度:平均、最好、最坏均为
O(nlogn) - 空间复杂度:需要引入辅助空间
O(n),如果是给链表排序则只需要O(1) - 描述:是个稳定的外部排序算法
- 时间复杂度:平均、最好、最坏均为
- 代码实现:
- 数组归并
class Solution { public:void merge(vector<int>&nums,vector<int>& arr,int left,int mid,int right){int l = left;//左边第一个未排序元素int r = mid+1;//右边第一个未排序元素int pos = left;//arr数组// 合并while(l<=mid&&r<=right){if(nums[l]<nums[r]) arr[pos++] = nums[l++];else arr[pos++] = nums[r++];}//合并剩余元素while(l<=mid) arr[pos++] = nums[l++];while(r<=right) arr[pos++] = nums[r++];//将临时数组进行拷贝while(left<=right){nums[left] = arr[left];left++;}}void mergeSort(vector<int>& nums,vector<int>& arr,int left,int right){ if(left>=right) return;int mid = (right+left)/2;mergeSort(nums,arr,left,mid);mergeSort(nums,arr,mid+1,right);merge(nums,arr,left,mid,right);}vector<int> sortArray(vector<int>& nums) {vector<int> arr(nums.size());mergeSort(nums,arr,0,nums.size()-1);return nums;} };- 链表归并:
1.4、冒泡排序
-
冒泡排序基本思想:每次循环将最大元素交换到最右边,每次内部循环都需要交换
-
和选择排序的区别:异曲同工,选择排序交换次数少,但是在数组有序的情况下,依旧需要完整的遍历完,时间复杂度稳定到
O(n^2),冒泡排序,可以在数组有序的情况下提前结束 -
复杂度:
- 时间复杂度:平均时间复杂度
O(n^2),最好时间复杂度O(n),平均时间复杂度O(n^2)- 空间复杂度:O(1) - 描述:是个稳定的内部排序
- 时间复杂度:平均时间复杂度
-
代码实现:
// 简单版本,和选择排序基本一致 class Solution { public:void bubbleSort(vector<int>& nums,int n){for(int i=nums.size()-1;i>=0;i--){for(int j=0;j<i;++j){if(nums[j]>nums[j+1]) swap(nums[j],nums[j+1]);}}}vector<int> sortArray(vector<int>& nums) {bubbleSort(nums,nums.size());return nums;} }; // 优化版本class Solution {public:void bubbleSort(vector<int>& nums,int n){bool flag = false;for(int i=nums.size()-1;i>=0;i--){flag = false;for(int j=0;j<i;++j) //一般过去是有序的,则时间复杂度只有O(n){if(nums[j]>nums[j+1]){swap(nums[j],nums[j+1]);flag = true;}}if(!flag) break;}}vector<int> sortArray(vector<int>& nums) {bubbleSort(nums,nums.size());return nums;}};
1.5、选择排序
-
选择排序基本思想:每次选择一个最大的元素排到后面,每次内部循环只需要交换一次
-
复杂度:
- 时间复杂度:最好、最坏、平均时间复杂度为O(n^2)
- 空间复杂度:没有辅助容器为O(1)
- 描述:是个不稳定的内部排序
-
代码实现:
class Solution { public:void selectSort(vector<int>& nums,int n){int Max=-1;for(int i=nums.size()-1;i>=0;i--){Max = i;for(int j=0;j<i;++j){if(nums[j]>nums[Max]) Max=j;}swap(nums[i],nums[Max]);}}vector<int> sortArray(vector<int>& nums) {selectSort(nums,nums.size());return nums;} };
1.6、插入排序
-
插入排序基本思想:每次将一个元素插入到前面维护好顺序的元素里面
-
复杂度:
- 时间复杂度:最坏、平均为
O(n^2),最好为O(n)-基本有序的情况 - 空间复杂度:O(1)
- 描述:是个稳定的内部排序算法
- 时间复杂度:最坏、平均为
-
代码实现:
class Solution { public:void InsertSort(vector<int>& nums,int n){for(int i=1;i<n;++i){// 每次将第i个元素插入到前i-1数组中int tmp = nums[i]; int j=i;while(j>0 && nums[j-1]>tmp){nums[j] = nums[j-1];--j;}nums[j] = tmp;}}vector<int> sortArray(vector<int>& nums) {InsertSort(nums,nums.size());return nums;} };
2、查找算法
2.1、二分查找
-
基本思想:前提是数组有序,通过中间点折半的思想实现快速的查找
-
红蓝边界思想:
int left = -1,right = N; // 数组下标从0到N-1 while left+1!=rightm = (left+right)/2;if IsBlue(m)left = m;else right = m; return left or right; //返回值根据题目要求来定 -
复杂度:
- 时间复杂度:
O(log n)
- 时间复杂度:
-
代码实现:
-
在有序数组中查找元素的下标:测试实列
class Solution { public:/*红蓝边界求值,时间复杂度O(log n)1.没有这个元素的话,且right进行了移动2.没有这个元素的话,且right没有进行移动3.有这个元素,直接返回right*/int search(vector<int>& nums, int target) {int left = -1;int right = nums.size();while(left+1!=right){int mid = (left+right)/2;if(nums[mid]<target) left = mid;else right = mid;}//需要判断对应的节点不存在的可能if(right==nums.size()||nums[right]!=target) return -1; else return right;} };
-