深度学习3：激活函数

一、激活函数的简介与由来

激活函数：是用来加入非线性因素的，解决线性模型所不能解决的问题。

线性函数的组合解决的问题太有限了，碰到非线性问题就束手无策了。如下图。

通过激活函数映射之后，可以输出非线性函数。

最后再通过最优化损失函数的做法，我们能够学习到不断学习靠近能够正确分类三角形和圆形点的曲线 。

二、激活函数的种类

它能够把输入的连续实值变换为0和1之间的输出，特别的，如果是非常大的负数，那么输出就是0；如果是非常大的正数，输出就是1.

缺点：

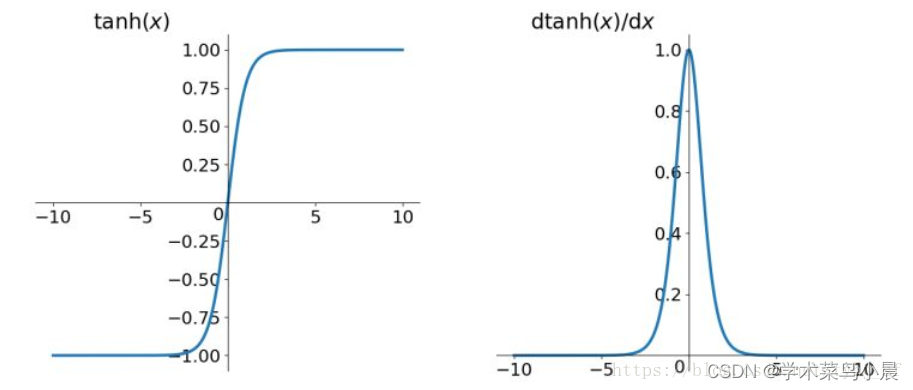
它解决了Sigmoid函数的不是zero-centered输出问题，然而，梯度消失（gradient vanishing）的问题和幂运算的问题仍然存在。

Relu=max(0,x)

ReLU函数其实就是一个取最大值函数.

解决了gradient vanishing问题 (在正区间)，计算速度非常快，只需要判断输入是否大于0，收敛速度远快于sigmoid和tanh。

缺点：

f(x)=max(αx,x)

Leaky ReLU有ReLU的所有优点，外加不会有Dead ReLU问题，但是在实际操作当中，并没有完全证明Leaky ReLU总是好于ReLU。

f(x) = x・tanh(ς(x))，其中， ς(x) = ln(1+e^x)，是一个softmax激活函数和。

在YOLOv4中使用Mish函数的原因是它的低成本和它的平滑、非单调、上无界、有下界等特点，与其他常用函数如ReLU和Swish相比，提高了它的性能。

类似的Swish函数（yolov5使用的激活函数）：

Mish函数优点：

无上界有有界：无上界是任何激活函数都需要的特性，因为它避免了导致训练速度急剧下降的梯度饱和。因此，加快训练过程。无下界属性有助于实现强正则化效果(适当的拟合模型)。(Mish的这个性质类似于ReLU和Swish的性质，其范围是[≈0.31，∞))。
非单调函数：这种性质有助于保持小的负值，从而稳定网络梯度流。大多数常用的激活函数，如ReLU [f(x) = max(0, x)]， Leaky ReLU [f(x) = max(0, x)， 1]，由于其差分为0，不能保持负值，因此大多数神经元没有得到更新。
无穷阶连续性和光滑性：Mish是光滑函数，具有较好的泛化能力和结果的有效优化能力，可以提高结果的质量。在图中，可以看到ReLU和Mish之间的一个随机初始化的神经网络在宏观平滑度上的剧烈变化。然而，在Swish和Mish的情况下，宏观上或多或少还是相似的。
计算量较大，但是效果更好：与ReLU相比，它的计算比较贵，但在深度神经网络中显示了比ReLU更好的结果。
自门控：此属性受到Swish函数的启发，其中标量输入被提供给gate。它优于像ReLU这样的点式激活函数，后者只接受单个标量输入，而不需要更改网络参数。