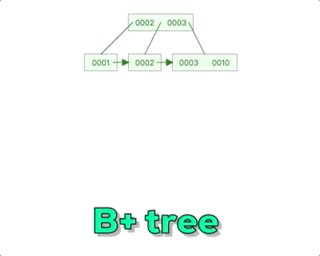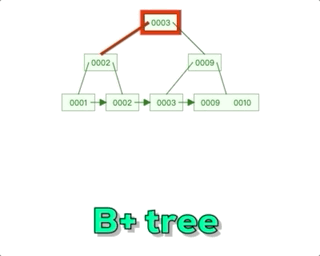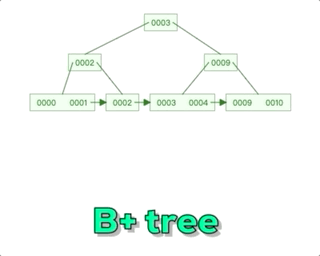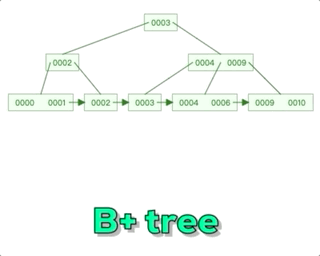
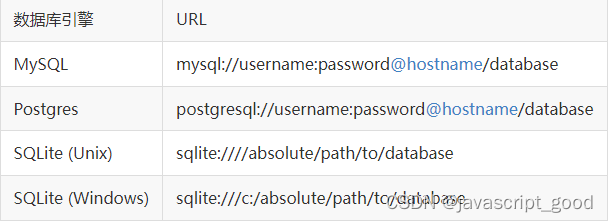
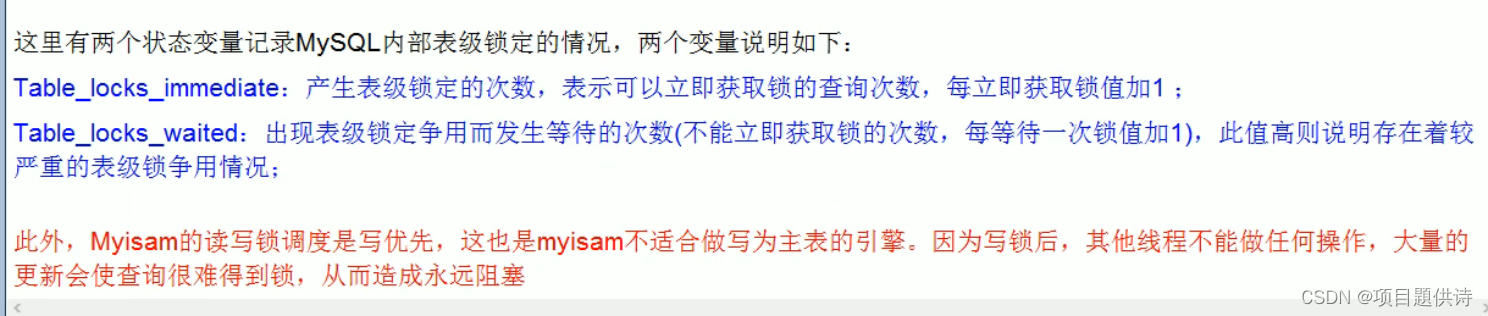
回溯算法团灭子集、组合、排列问题
根据元素是否重复和是否可复选，分为以下三种变体：
1、元素无重不可复选
2、元素有重不可复选
3、元素无重可复选

该篇给出第三种情况的代码，另外两种的实现见上方变体链接。

class NoRepeatAndMultiple:"""元素无重可复选"""def subsets(self, nums: List[int], target) -> List[List[int]]:"""子集问题:param nums::return:"""self.res = []self.track = []self.track_sum = 0self.s_backtrack(nums, 0, target)return self.resdef s_backtrack(self, nums, start, target):#  base caseif self.track_sum == target:self.res.append(self.track[:])return# base caseif self.track_sum > target:returnfor i in range(start, len(nums)):# 做选择self.track_sum += nums[i]self.track.append(nums[i])# 通过 start 参数控制树枝的遍历，避免产⽣重复的⼦集self.s_backtrack(nums, i, target)# 撤销选择self.track_sum -= nums[i]self.track.pop()def combination(self, nums: List[int], k: int) -> List[List[int]]:"""组合问题，这里等价于子集问题:param nums::param k::return:"""passdef permute(self, nums: List[int]) -> List[List[int]]:"""排列问题:param nums::return:"""self.res = []self.track = []self.p_backtrack(nums)return self.resdef p_backtrack(self, nums):#  base caseif len(self.track) == len(nums):self.res.append(self.track[:])returnfor i in range(0, len(nums)):# 做选择self.track.append(nums[i])# 通过 start 参数控制树枝的遍历，避免产⽣重复的⼦集self.p_backtrack(nums)# 撤销选择self.track.pop()