数据结构与算法基础-学习-29-图之关键路径

 图的其他相关知识点和源码分享可以参考之前的博客：   

《数据结构与算法基础-学习-23-图之邻接矩阵与邻接表》，

《数据结构与算法基础-学习-24-图的遍历之DFS（深度优先搜索）和BFS（广度优先搜索）》，

《数据结构与算法基础-学习-25-图之MST（最小代价生成树）之Prim（普利姆）算法》，

《数据结构与算法基础-学习-26-图之MST（最小代价生成树）之Kluskal（克鲁斯卡尔）算法》，

《数据结构与算法基础-学习-27-图之最短路径之Dijkstra（迪杰斯特拉）算法》，

《数据结构与算法基础-学习-28-图之拓扑排序》

一、相关定义

1、把工程计划表示为边表示活动的网络，即AOE网，用顶点表示事件，弧表示活动，弧的权表示活动持续时间。

2、事件表示在它之前的活动已经完成，在它之后的活动可以开始。

3、关键路径：路径长度最长的路径。

4、路径长度：路径上个活动持续时间之和。

二、个人理解

1、关键路径表示一个工程的话，例如做饭，开始做饭表示整个工程开始，结束做饭表示整个工程结束，也就是说只一个起点或者叫源点（入度为0的顶点），只有一个终点或者叫汇点（出度为0的顶点）。

2、我们在进行关键路径计算时，需要判断：

（1）这是不是一个有向图。

（2）是不是无环（可以通过拓扑排序来判断）。

（3）是不是只有一个源点和一个终点。

三、解决了那些事

1、完成整项工程至少需要花费多少时间。

2、哪些活动是影响工程进度的关键。

四、描述量

名称描述
ve(vj)表示事件（顶点）vj的最早发生时间。
vl(vj)表示事件（顶点）vj的最迟发生时间。
e(i)表示活动（弧）ai的最早开始时间。
l(i)表示活动（弧）ai的最迟开始时间。

五、公式

1、ve(j) = Max(ve(i) + w(i,j)),表示i->j的情况下。

2、vl(i) = Min(vl(j) - w(i,j)),表示i->j的情况下。

3、e(i) = ve(j),表示j->k，第i各活动的情况下。

4、l(i) = vl(k) - w(j,k),表示j->k，第i各活动的情况下。

六、关键路径算法思路

​

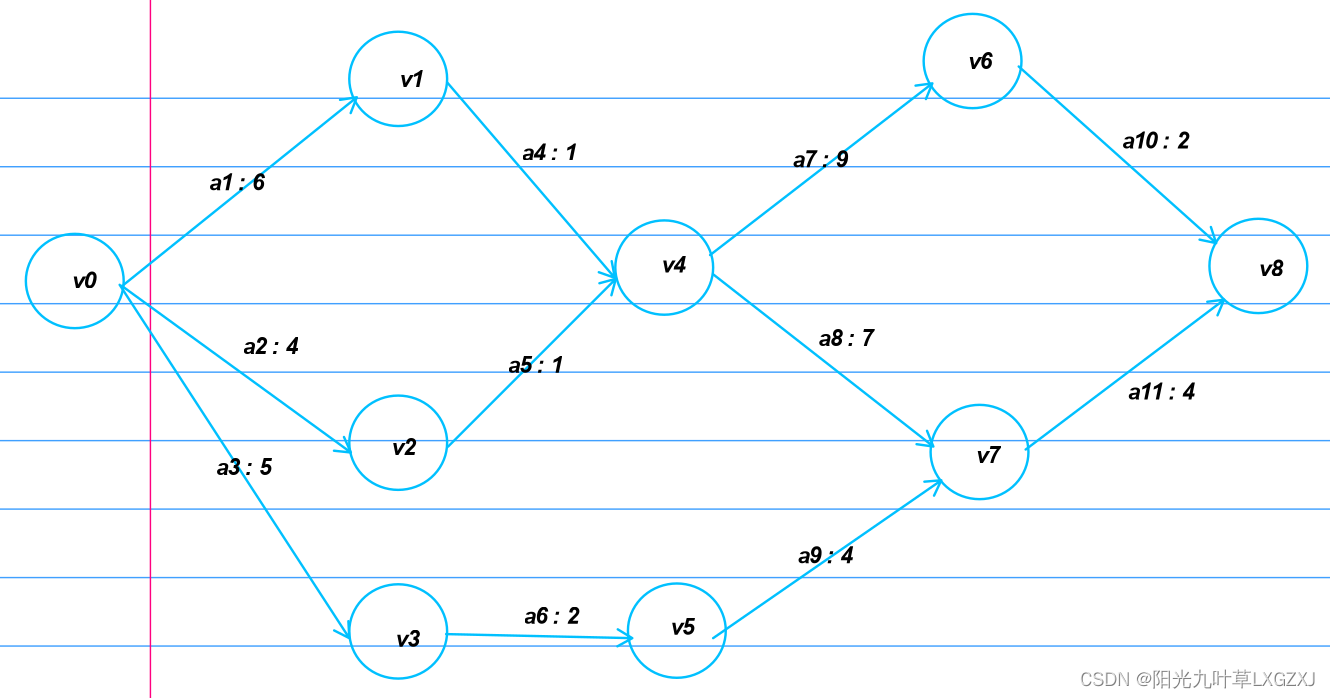
 我这边是结合邻接矩阵实现的，生成邻接矩阵如下：

2023-8-23 9:33:49--[ Debug ]--Printf AMGraph                     :
VertexArray    : [0 ,1 ,2 ,3 ,4 ,5 ,6 ,7 ,8 ]
ArcArray       :
0  : [32767 ,6     ,4     ,5     ,32767 ,32767 ,32767 ,32767 ,32767 ]
1  : [32767 ,32767 ,32767 ,32767 ,1     ,32767 ,32767 ,32767 ,32767 ]
2  : [32767 ,32767 ,32767 ,32767 ,1     ,32767 ,32767 ,32767 ,32767 ]
3  : [32767 ,32767 ,32767 ,32767 ,32767 ,2     ,32767 ,32767 ,32767 ]
4  : [32767 ,32767 ,32767 ,32767 ,32767 ,32767 ,9     ,7     ,32767 ]
5  : [32767 ,32767 ,32767 ,32767 ,32767 ,32767 ,32767 ,4     ,32767 ]
6  : [32767 ,32767 ,32767 ,32767 ,32767 ,32767 ,32767 ,32767 ,2     ]
7  : [32767 ,32767 ,32767 ,32767 ,32767 ,32767 ,32767 ,32767 ,4     ]
8  : [32767 ,32767 ,32767 ,32767 ,32767 ,32767 ,32767 ,32767 ,32767 ]
InduityArray   : [0 ,1 ,1 ,1 ,2 ,1 ,1 ,2 ,2 ]
OutdegreeArray : [3 ,1 ,1 ,1 ,2 ,1 ,1 ,1 ,0 ]
CurVertexNum   : 9
CurArcNum      : 11

在之前分享的邻接矩阵代码的基础上增加了入度InduityArray和出度OutdegreeArray，为了方便计算。

1、计算事件最早发生时间

2023-8-23 9:46:19--[ Debug ]--SqQueue Data   :
Data           : [ 0 ,-1 ,-1 ,-1 ,-1 ,-1 ,-1 ,-1 ,-1 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 9
SqQueueMaxLen  : 9
Flag           : INT_TYPE_FLAG

初始化一个事件最早发生的队列，不一定是队列，数组也行。源点的最早发生时间是0，填入到队列中，其他值还不确定所以先初始化-1。

2023-8-23 9:56:37--[ Debug ]--Printf SqStack
Data           : [ 0 ]
Flag           : INT_TYPE_FLAG
2023-8-23 9:56:37--[ Debug ]--Printf HashTable
DataNum : 1     , [ (0,(nil)) ]
DataNum : 0     , [(nil)]
DataNum : 0     , [(nil)]
DataNum : 0     , [(nil)]
DataNum : 0     , [(nil)]
DataNum : 0     , [(nil)]
DataNum : 0     , [(nil)]
DataNum : 0     , [(nil)]
DataNum : 0     , [(nil)]
TotalDataNum : 1     
ArrayMaxLen  : 9

还需要两个访问数组，分别是用哈希表和栈实现的，为什么要用两个呢，因为一个用来快速访问节点是否访问过。一个用来进行节点回溯。后面看着看着就会领悟的。我们先把访问过的源点0压入两个访问数组中。

进入一个大循环，循环退出条件为所有节点都被访问过。

栈中压出第一个节点0，然后我们在邻接矩阵中扫描第0行。我们可以扫描到三个边a1、a2、a3，且他们对应的终点V1、V2、V3的入度都是1，根据公式ve(j) = Max(ve(i) + w(i,j))。

（1）0->1，ve(1) = Max(ve(0) + w(0,1)) = 0 + 6 = 6

（2）0->2，ve(2) = Max(ve(0) + w(0,2)) = 0 + 4 = 4

（3）0->3，ve(3) = Max(ve(0) + w(0,3)) = 0 + 5 = 5

这三个点都访问过，我们都压入访问数组中，具体如下：

2023-8-23 9:56:37--[ Debug ]--SqQueue Data   :
Data           : [ 0 ,6 ,4 ,5 ,-1 ,-1 ,-1 ,-1 ,-1 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 9
SqQueueMaxLen  : 9
Flag           : INT_TYPE_FLAG
2023-8-23 9:56:37--[ Debug ]--Printf SqStack
Data           : [ 1 ,2 ,3 ]
Flag           : INT_TYPE_FLAG
2023-8-23 9:56:37--[ Debug ]--Printf HashTable
DataNum : 1     , [ (0,(nil)) ]
DataNum : 1     , [ (1,(nil)) ]
DataNum : 1     , [ (2,(nil)) ]
DataNum : 1     , [ (3,(nil)) ]
DataNum : 0     , [(nil)]
DataNum : 0     , [(nil)]
DataNum : 0     , [(nil)]
DataNum : 0     , [(nil)]
DataNum : 0     , [(nil)]
TotalDataNum : 4     
ArrayMaxLen  : 9

第0行都已经遍历完，我们压出栈的下一个元素3，然后我们在邻接矩阵中扫描第3行。

我们可以扫描到边a6，且对应的终点V6的入度是1，根据公式ve(j) = Max(ve(i) + w(i,j))。

（1）3->5，ve(5) = Max(ve(3) + w(3,5)) = 5 + 2 = 7

这个点访问过，我们压入访问数组中，具体如下：

2023-8-23 9:56:37--[ Debug ]--SqQueue Data   :
Data           : [ 0 ,6 ,4 ,5 ,-1 ,7 ,-1 ,-1 ,-1 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 9
SqQueueMaxLen  : 9
Flag           : INT_TYPE_FLAG
2023-8-23 9:56:37--[ Debug ]--Printf SqStack
Data           : [ 1 ,2 ,5 ]
Flag           : INT_TYPE_FLAG
2023-8-23 9:56:37--[ Debug ]--Printf HashTable
DataNum : 1     , [ (0,(nil)) ]
DataNum : 1     , [ (1,(nil)) ]
DataNum : 1     , [ (2,(nil)) ]
DataNum : 1     , [ (3,(nil)) ]
DataNum : 0     , [(nil)]
DataNum : 1     , [ (5,(nil)) ]
DataNum : 0     , [(nil)]
DataNum : 0     , [(nil)]
DataNum : 0     , [(nil)]
TotalDataNum : 5     
ArrayMaxLen  : 9

第3行都已经遍历完，我们压出栈的下一个元素5，然后我们在邻接矩阵中扫描第5行。

我们可以扫描到边a9，且对应的终点V7的入度是2，且V7的另一条入度边a8的起点V4没有访问过，所以不能计算V7的事件最早发生时间。

具体如下：

2023-8-23 9:56:37--[ Debug ]--SqQueue Data   :
Data           : [ 0 ,6 ,4 ,5 ,-1 ,7 ,-1 ,-1 ,-1 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 9
SqQueueMaxLen  : 9
Flag           : INT_TYPE_FLAG
2023-8-23 9:56:37--[ Debug ]--Printf SqStack
Data           : [ 1 ,2 ]
Flag           : INT_TYPE_FLAG
2023-8-23 9:56:37--[ Debug ]--Printf HashTable
DataNum : 1     , [ (0,(nil)) ]
DataNum : 1     , [ (1,(nil)) ]
DataNum : 1     , [ (2,(nil)) ]
DataNum : 1     , [ (3,(nil)) ]
DataNum : 0     , [(nil)]
DataNum : 1     , [ (5,(nil)) ]
DataNum : 0     , [(nil)]
DataNum : 0     , [(nil)]
DataNum : 0     , [(nil)]
TotalDataNum : 5     
ArrayMaxLen  : 9

第5行都已经遍历完，我们压出栈的下一个元素2，然后我们在邻接矩阵中扫描第2行。

我们可以扫描到边a5，且对应的终点V4的入度是2，V4入度边的起点V1和V2我们都是访问过的，可以计算事件最早发生时间，根据公式ve(j) = Max(ve(i) + w(i,j))。

（1）1->4，2->4，ve(4) = Max(ve(1) + w(1,4)，ve(2) + w(2,4)) = Max(6 +1，4 + 1) = Max(7，5) = 7

这个点访问过，我们压入访问数组中，具体如下：

2023-8-23 9:56:37--[ Debug ]--SqQueue Data   :
Data           : [ 0 ,6 ,4 ,5 ,7 ,7 ,-1 ,-1 ,-1 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 9
SqQueueMaxLen  : 9
Flag           : INT_TYPE_FLAG
2023-8-23 9:56:37--[ Debug ]--Printf SqStack
Data           : [ 1 ,4 ]
Flag           : INT_TYPE_FLAG
2023-8-23 9:56:37--[ Debug ]--Printf HashTable
DataNum : 1     , [ (0,(nil)) ]
DataNum : 1     , [ (1,(nil)) ]
DataNum : 1     , [ (2,(nil)) ]
DataNum : 1     , [ (3,(nil)) ]
DataNum : 1     , [ (4,(nil)) ]
DataNum : 1     , [ (5,(nil)) ]
DataNum : 0     , [(nil)]
DataNum : 0     , [(nil)]
DataNum : 0     , [(nil)]
TotalDataNum : 6     
ArrayMaxLen  : 9

第2行都已经遍历完，我们压出栈的下一个元素4，然后我们在邻接矩阵中扫描第4行。

我们可以扫描到边a7，a8，V6的入度是1我们可以直接计算事件最早发生，a8对应的终点V7的入度是2，V7入度边的起点V4和V5我们都是访问过的，可以计算事件最早发生时间，根据公式ve(j) = Max(ve(i) + w(i,j))。

（1）4->6，ve(6) = Max(ve(4) + w(4,6)) = Max(7 + 9) = 16

（2）4->7，5->7，ve(7) = Max(ve(4) + w(4,7)，ve(5) + w(5,7)) = Max(7 +7，7 + 4) = Max(14，11) = 14

这些点访问过，我们压入访问数组中，具体如下：

2023-8-23 9:56:37--[ Debug ]--SqQueue Data   :
Data           : [ 0 ,6 ,4 ,5 ,7 ,7 ,16 ,14 ,-1 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 9
SqQueueMaxLen  : 9
Flag           : INT_TYPE_FLAG
2023-8-23 9:56:37--[ Debug ]--Printf SqStack
Data           : [ 1 ,6 ,7 ]
Flag           : INT_TYPE_FLAG
2023-8-23 9:56:37--[ Debug ]--Printf HashTable
DataNum : 1     , [ (0,(nil)) ]
DataNum : 1     , [ (1,(nil)) ]
DataNum : 1     , [ (2,(nil)) ]
DataNum : 1     , [ (3,(nil)) ]
DataNum : 1     , [ (4,(nil)) ]
DataNum : 1     , [ (5,(nil)) ]
DataNum : 1     , [ (6,(nil)) ]
DataNum : 1     , [ (7,(nil)) ]
DataNum : 0     , [(nil)]
TotalDataNum : 8     
ArrayMaxLen  : 9

第4行都已经遍历完，我们压出栈的下一个元素7，然后我们在邻接矩阵中扫描第7行。

我们可以扫描到边a11，V8入度边的起点V6和V7我们都是访问过的，可以计算事件最早发生时间，根据公式ve(j) = Max(ve(i) + w(i,j))。

（1）6->8，7->8，ve(8) = Max(ve(6) + w(6,8)，ve(7) + w(7,8)) = Max(16 +2，14 + 4) = Max(18，18) = 18

这些点访问过，我们压入访问数组中，具体如下：

2023-8-23 9:56:37--[ Debug ]--SqQueue Data   :
Data           : [ 0 ,6 ,4 ,5 ,7 ,7 ,16 ,14 ,18 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 9
SqQueueMaxLen  : 9
Flag           : INT_TYPE_FLAG
2023-8-23 9:56:37--[ Debug ]--Printf SqStack
Data           : [ 1 ,6 ,8 ]
Flag           : INT_TYPE_FLAG
2023-8-23 9:56:37--[ Debug ]--Printf HashTable
DataNum : 1     , [ (0,(nil)) ]
DataNum : 1     , [ (1,(nil)) ]
DataNum : 1     , [ (2,(nil)) ]
DataNum : 1     , [ (3,(nil)) ]
DataNum : 1     , [ (4,(nil)) ]
DataNum : 1     , [ (5,(nil)) ]
DataNum : 1     , [ (6,(nil)) ]
DataNum : 1     , [ (7,(nil)) ]
DataNum : 1     , [ (8,(nil)) ]
TotalDataNum : 9     
ArrayMaxLen  : 9

所有点被访问完了，事件最早发生时间也就被算出来了。

2、事件最迟发生时间

事件最迟发生时间和事件最早发生时间的计算上的区别：

1、事件最早发生时间是从起点到源点，事件最迟发生时间反之从源点到起点。

2、事件最早发生时间是横向扫描邻接矩阵，事件最迟发生时间反之是纵向扫描。

3、事件最早发生时间是根据入度进行相关判断，事件最迟发生时间反之是根据出度判断。

源点的事件最迟发生时间和起点是一样的，都是18，我们先填入18和节点8，如下：

2023-8-23 14:6:28--[ Debug ]--SqQueue Data   :
Data           : [ -1 ,-1 ,-1 ,-1 ,-1 ,-1 ,-1 ,-1 ,18 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 9
SqQueueMaxLen  : 9
Flag           : INT_TYPE_FLAG
2023-8-23 14:6:28--[ Debug ]--Printf SqStack
Data           : [ 8 ]
Flag           : INT_TYPE_FLAG
2023-8-23 14:6:28--[ Debug ]--Printf HashTable
DataNum : 0     , [(nil)]
DataNum : 0     , [(nil)]
DataNum : 0     , [(nil)]
DataNum : 0     , [(nil)]
DataNum : 0     , [(nil)]
DataNum : 0     , [(nil)]
DataNum : 0     , [(nil)]
DataNum : 0     , [(nil)]
DataNum : 1     , [ (8,(nil)) ]
TotalDataNum : 1     
ArrayMaxLen  : 9

进入循环，我们从栈中压出节点8，开始纵向扫描节点8，发现6和7节点，且他们的出度都是1，根据公式vl(j) = Min(vl(j) - w(i,j))，进行计算：

（1）6->8，vl(6) = Min(vl(8) - w(6,8)) = Min(18 - 2) = 16

（2）7->8，vl(7) = Min(vl(8) - w(7,8)) = Min(18 - 4) = 14

这些点访问过，我们压入访问数组中，具体如下：

2023-8-23 14:6:28--[ Debug ]--SqQueue Data   :
Data           : [ -1 ,-1 ,-1 ,-1 ,-1 ,-1 ,16 ,14 ,18 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 9
SqQueueMaxLen  : 9
Flag           : INT_TYPE_FLAG
2023-8-23 14:6:28--[ Debug ]--Printf SqStack
Data           : [ 6 ,7 ]
Flag           : INT_TYPE_FLAG
2023-8-23 14:6:28--[ Debug ]--Printf HashTable
DataNum : 0     , [(nil)]
DataNum : 0     , [(nil)]
DataNum : 0     , [(nil)]
DataNum : 0     , [(nil)]
DataNum : 0     , [(nil)]
DataNum : 0     , [(nil)]
DataNum : 1     , [ (6,(nil)) ]
DataNum : 1     , [ (7,(nil)) ]
DataNum : 1     , [ (8,(nil)) ]
TotalDataNum : 3     
ArrayMaxLen  : 9

继续进入循环，我们从栈中压出节点7，开始纵向扫描节点7，发现4和5节点，5的出度是1，可以直接计算，4的出度是2，且节点6和7都已经访问过了，也可以计算，根据公式vl(j) = Min(vl(j) - w(i,j))，进行计算：

（1）4->6，4->7，vl(4) = Min(vl(6) - w(4,6)，vl(7) - w(4,7)) = Min(16 - 9，14 - 7) = 7

（2）5->7，vl(5) = Min(vl(7) - w(5,7)) = Min(14 - 4) = 10

这些点访问过，我们压入访问数组中，具体如下：

2023-8-23 14:6:28--[ Debug ]--SqQueue Data   :
Data           : [ -1 ,-1 ,-1 ,-1 ,7 ,10 ,16 ,14 ,18 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 9
SqQueueMaxLen  : 9
Flag           : INT_TYPE_FLAG
2023-8-23 14:6:28--[ Debug ]--Printf SqStack
Data           : [ 6 ,4 ,5 ]
Flag           : INT_TYPE_FLAG
2023-8-23 14:6:28--[ Debug ]--Printf HashTable
DataNum : 0     , [(nil)]
DataNum : 0     , [(nil)]
DataNum : 0     , [(nil)]
DataNum : 0     , [(nil)]
DataNum : 1     , [ (4,(nil)) ]
DataNum : 1     , [ (5,(nil)) ]
DataNum : 1     , [ (6,(nil)) ]
DataNum : 1     , [ (7,(nil)) ]
DataNum : 1     , [ (8,(nil)) ]
TotalDataNum : 5     
ArrayMaxLen  : 9

继续进入循环，我们从栈中压出节点5，开始纵向扫描节点5，发现3节点，3的出度是1，可以直接计算，根据公式vl(j) = Min(vl(j) - w(i,j))，进行计算：

（1）3->5，vl(3) = Min(vl(5) - w(3,5)) = Min(10 - 2) = 8

这些点访问过，我们压入访问数组中，具体如下：

2023-8-23 14:6:28--[ Debug ]--SqQueue Data   :
Data           : [ -1 ,-1 ,-1 ,8 ,7 ,10 ,16 ,14 ,18 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 9
SqQueueMaxLen  : 9
Flag           : INT_TYPE_FLAG
2023-8-23 14:6:28--[ Debug ]--Printf SqStack
Data           : [ 6 ,4 ,3 ]
Flag           : INT_TYPE_FLAG
2023-8-23 14:6:28--[ Debug ]--Printf HashTable
DataNum : 0     , [(nil)]
DataNum : 0     , [(nil)]
DataNum : 0     , [(nil)]
DataNum : 1     , [ (3,(nil)) ]
DataNum : 1     , [ (4,(nil)) ]
DataNum : 1     , [ (5,(nil)) ]
DataNum : 1     , [ (6,(nil)) ]
DataNum : 1     , [ (7,(nil)) ]
DataNum : 1     , [ (8,(nil)) ]
TotalDataNum : 6     
ArrayMaxLen  : 9

继续进入循环，我们从栈中压出节点3，开始纵向扫描节点3，发现0节点，0的出度是3，发现1号点没有访问过直接退出当前循环，后面的2，3不需要扫描，因为一个没访问就不可以进行计算。

具体如下：

2023-8-23 14:6:28--[ Debug ]--SqQueue Data   :
Data           : [ -1 ,-1 ,-1 ,8 ,7 ,10 ,16 ,14 ,18 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 9
SqQueueMaxLen  : 9
Flag           : INT_TYPE_FLAG
2023-8-23 14:6:28--[ Debug ]--Printf SqStack
Data           : [ 6 ,4 ]
Flag           : INT_TYPE_FLAG
2023-8-23 14:6:28--[ Debug ]--Printf HashTable
DataNum : 0     , [(nil)]
DataNum : 0     , [(nil)]
DataNum : 0     , [(nil)]
DataNum : 1     , [ (3,(nil)) ]
DataNum : 1     , [ (4,(nil)) ]
DataNum : 1     , [ (5,(nil)) ]
DataNum : 1     , [ (6,(nil)) ]
DataNum : 1     , [ (7,(nil)) ]
DataNum : 1     , [ (8,(nil)) ]
TotalDataNum : 6     
ArrayMaxLen  : 9

继续进入循环，我们从栈中压出节点4，开始纵向扫描节点4，发现1，2节点，且出度都是1，可以直接计算，根据公式vl(j) = Min(vl(j) - w(i,j))，进行计算：

（1）1->4，vl(1) = Min(vl(4) - w(1,4)) = Min(7 - 1) = 6

（2）2->4，vl(2) = Min(vl(4) - w(2,4)) = Min(7 - 1) = 6

这些点访问过，我们压入访问数组中，具体如下：

2023-8-23 14:6:28--[ Debug ]--SqQueue Data   :
Data           : [ -1 ,6 ,6 ,8 ,7 ,10 ,16 ,14 ,18 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 9
SqQueueMaxLen  : 9
Flag           : INT_TYPE_FLAG
2023-8-23 14:6:28--[ Debug ]--Printf SqStack
Data           : [ 6 ,1 ,2 ]
Flag           : INT_TYPE_FLAG
2023-8-23 14:6:28--[ Debug ]--Printf HashTable
DataNum : 0     , [(nil)]
DataNum : 1     , [ (1,(nil)) ]
DataNum : 1     , [ (2,(nil)) ]
DataNum : 1     , [ (3,(nil)) ]
DataNum : 1     , [ (4,(nil)) ]
DataNum : 1     , [ (5,(nil)) ]
DataNum : 1     , [ (6,(nil)) ]
DataNum : 1     , [ (7,(nil)) ]
DataNum : 1     , [ (8,(nil)) ]
TotalDataNum : 8     
ArrayMaxLen  : 9

继续进入循环，我们从栈中压出节点2，开始纵向扫描节点2，发现0节点，且出度都是3，1，2，3节点都被访问过，可以直接计算，根据公式vl(j) = Min(vl(j) - w(i,j))，进行计算：

（1）0->1，0->2，0->3，vl(0) = Min(vl(1) - w(0,1)，vl(2) - w(0,2)，vl(3) - w(0,4)) = Min(6 - 6，6 - 4，8 - 5) = Min(0，2，3) = 0

这些点访问过，我们压入访问数组中，具体如下：

2023-8-23 14:6:28--[ Debug ]--SqQueue Data   :
Data           : [ 0 ,6 ,6 ,8 ,7 ,10 ,16 ,14 ,18 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 9
SqQueueMaxLen  : 9
Flag           : INT_TYPE_FLAG
2023-8-23 14:6:28--[ Debug ]--Printf SqStack
Data           : [ 6 ,1 ,0 ]
Flag           : INT_TYPE_FLAG
2023-8-23 14:6:28--[ Debug ]--Printf HashTable
DataNum : 1     , [ (0,(nil)) ]
DataNum : 1     , [ (1,(nil)) ]
DataNum : 1     , [ (2,(nil)) ]
DataNum : 1     , [ (3,(nil)) ]
DataNum : 1     , [ (4,(nil)) ]
DataNum : 1     , [ (5,(nil)) ]
DataNum : 1     , [ (6,(nil)) ]
DataNum : 1     , [ (7,(nil)) ]
DataNum : 1     , [ (8,(nil)) ]
TotalDataNum : 9     
ArrayMaxLen  : 9

所有点被访问完了，事件最迟发生时间也就被算出来了。

3、活动最早开始、最迟时间，关键路径

有了事件最迟发生时间和事件最早发生时间，活动最早开始、最迟时间，关键路径就好算了，直接套公式。

我们一条边一条边来。

关键路径我是活动最早开始事件 - 活动最迟开始事件，所以是负值，但不影响取关键路径。

弧信息活动最早开始事件活动最迟开始事件关键路径
a1边，0->1e(1) = ve(0) = 0

l(1) = vl(1) - w(0,1) = 0

0 - 0 = 0
a2边，0->2e(2) = ve(0) = 0

l(2) = vl(2) - w(0,2) = 2

0 - 2 = -2
a3边，0->3e(3) = ve(0) = 0

l(3) = vl(3) - w(0,3) = 3

0 - 3 = -3
a4边，1->4e(4) = ve(1) = 6

l(4) = vl(4) - w(1,4) = 6

6 - 6 = 0
a5边，2->4e(5) = ve(2) = 4

l(5) = vl(4) - w(2,4) = 6

4 - 6 = -2
a6边，3->5e(6) = ve(3) = 5

l(6) = vl(5) - w(3,5) = 8

5 - 8 = -3
a7边，4->6e(7) = ve(4) = 7

l(7) = vl(6) - w(4,6) = 7

7 - 7 = 0
a8边，4->7e(8) = ve(4) = 7

l(8) = vl(7) - w(4,7) = 7

7 - 7 = 0
a9边，5->7e(9) = ve(5) = 7

l(9) = vl(7) - w(5,7) = 10

7 - 10 = -3
a10边，6->8e(10) = ve(6) = 16

l(10) = vl(8) - w(6,8) = 16

16 - 16 = 0
a11边，7->8e(11) = ve(7) = 14

l(11) = vl(8) - w(7,8) = 14

14 - 14 = 0

七、自定义宏定义

#define CRITICAL_PATH_INIT_VAL -1

八、自定义结构体

typedef struct CriticalPathEventSt
{SqQueue* VertexEarlyQueue;    //事件最早发生权值或时间的队列。公式：ve(j) = Max(ve(i) + w(i,j)),表示i->j的情况下。SqQueue* VertexLateQueue;     //事件最晚发生权值或时间的队列。公式：vl(i) = Min(vl(j) - w(i,j)),表示i->j的情况下。
}CriticalPathEventSt;typedef struct CriticalPathActivitySt
{SqQueue* ArcStartVertexQueue; //存放活动（弧）的起始节点索引的队列。SqQueue* ArcEndVertexQueue;   //存放活动（弧）的结束节点索引的队列。SqQueue* ArcEarlyQueue;       //活动最早发生权值或时间的队列。公式：e(i) = ve(j),表示j->k，第i各活动的情况下。SqQueue* ArcLateQueue;        //活动最晚发生权值或时间的队列。公式：l(i) = vl(k) - w(j,k),表示j->k，第i各活动的情况下。SqQueue* CriticalPathQueue;   //关键路径的队列。
}CriticalPathActivitySt;typedef struct CriticalPathSt
{CriticalPathEventSt*    Event;CriticalPathActivitySt* Activity;
}CriticalPathSt;

九、自定义函数

1、InitCriticalPathEventSt

Status InitCriticalPathEventSt(CriticalPathEventSt** CpEvent, VertexIndexType ArrayMaxLen)
{JudgeAllNullPointer(CpEvent);*CpEvent                     = (CriticalPathEventSt*)MyMalloc(sizeof(CriticalPathEventSt));(*CpEvent)->VertexEarlyQueue = NULL;(*CpEvent)->VertexLateQueue  = NULL;InitSqQueue(&((*CpEvent)->VertexEarlyQueue),ArrayMaxLen,INT_TYPE_FLAG);InitSqQueue(&((*CpEvent)->VertexLateQueue),ArrayMaxLen,INT_TYPE_FLAG);LogFormat(Debug, "%s\n", "Init Critical Path Event St OK.");return SuccessFlag;
}

2、DestroyCriticalPathEventSt

Status DestroyCriticalPathEventSt(CriticalPathEventSt** CpEvent)
{JudgeAllNullPointer(*CpEvent);DestroySqQueue(&((*CpEvent)->VertexEarlyQueue));DestroySqQueue(&((*CpEvent)->VertexLateQueue));(*CpEvent)->VertexEarlyQueue = NULL;(*CpEvent)->VertexLateQueue  = NULL;free(*CpEvent);*CpEvent                     = NULL;LogFormat(Debug, "%s\n", "Destroy Critical Path Event St OK.");return SuccessFlag;
}

3、InitCriticalPathActivitySt

Status InitCriticalPathActivitySt(CriticalPathActivitySt** CpActivity, VertexIndexType ArrayMaxLen)
{JudgeAllNullPointer(CpActivity);*CpActivity                        = (CriticalPathActivitySt*)MyMalloc(sizeof(CriticalPathActivitySt));(*CpActivity)->ArcStartVertexQueue = NULL;(*CpActivity)->ArcEndVertexQueue   = NULL;(*CpActivity)->ArcEarlyQueue       = NULL;(*CpActivity)->ArcLateQueue        = NULL;(*CpActivity)->CriticalPathQueue   = NULL;InitSqQueue(&((*CpActivity)->ArcStartVertexQueue),ArrayMaxLen,INT_TYPE_FLAG);InitSqQueue(&((*CpActivity)->ArcEndVertexQueue),ArrayMaxLen,INT_TYPE_FLAG);InitSqQueue(&((*CpActivity)->ArcEarlyQueue),ArrayMaxLen,INT_TYPE_FLAG);InitSqQueue(&((*CpActivity)->ArcLateQueue),ArrayMaxLen,INT_TYPE_FLAG);InitSqQueue(&((*CpActivity)->CriticalPathQueue),ArrayMaxLen,INT_TYPE_FLAG);LogFormat(Debug, "%s\n", "Init Critical Path Activity St OK.");return SuccessFlag;
}

4、DestroyCriticalPathActivitySt

Status DestroyCriticalPathActivitySt(CriticalPathActivitySt** CpActivity)
{JudgeAllNullPointer(*CpActivity);DestroySqQueue(&((*CpActivity)->ArcStartVertexQueue));DestroySqQueue(&((*CpActivity)->ArcEndVertexQueue));DestroySqQueue(&((*CpActivity)->ArcEarlyQueue));DestroySqQueue(&((*CpActivity)->ArcLateQueue));DestroySqQueue(&((*CpActivity)->CriticalPathQueue));(*CpActivity)->ArcStartVertexQueue = NULL;(*CpActivity)->ArcEndVertexQueue   = NULL;(*CpActivity)->ArcEarlyQueue       = NULL;(*CpActivity)->ArcLateQueue        = NULL;(*CpActivity)->CriticalPathQueue   = NULL;free(*CpActivity);*CpActivity = NULL;LogFormat(Debug, "%s\n", "Destroy Critical Path Activity St OK.");return SuccessFlag;
}

5、InitCriticalPathSt

Status InitCriticalPathSt(CriticalPathSt** CP, AMGraph* AMG)
{JudgeAllNullPointer(CP);JudgeAllNullPointer(AMG);if (AMG->DirectionFlag == NET_UNDIRECTION_FLAG)//关键路径只支持有向网。{LogFormat(Warning,"Critical Path Init Only Support Directed Net, Exit.");return FailFlag;}*CP             = (CriticalPathSt*)MyMalloc(sizeof(CriticalPathSt));(*CP)->Event    = NULL;(*CP)->Activity = NULL;InitCriticalPathEventSt(&((*CP)->Event), AMG->CurVertexNum);InitCriticalPathActivitySt(&((*CP)->Activity), AMG->CurArcNum);LogFormat(Debug, "%s\n", "Init Critical Path St OK.");return SuccessFlag;
}

6、DestroyCriticalPathSt

Status DestroyCriticalPathSt(CriticalPathSt** CP)
{JudgeAllNullPointer(*CP);DestroyCriticalPathEventSt(&((*CP)->Event));DestroyCriticalPathActivitySt(&((*CP)->Activity));(*CP)->Event    = NULL;(*CP)->Activity = NULL;free(*CP);*CP             = NULL;LogFormat(Debug, "%s\n", "Destroy Critical Path St OK.");return SuccessFlag;
}

7、CheckCriticalPathAmgIllegal

//检查邻接矩阵是否适用于关键路径算法，只有一个起点和一个汇点。
//检查起点是否合法。
Status CheckCriticalPathAmgIllegal(AMGraph* AMG, VertexIndexType StartVertexIndex)
{JudgeAllNullPointer(AMG);//判断起始节点StartVertexIndex是否是在顶点索引范围内，不在，退出函数。if (StartVertexIndex < 0 || StartVertexIndex >= (AMG->CurVertexNum)){LogFormat(Debug,"StartVertexIndex : %d Is Illegal Node.\n",StartVertexIndex);return FailFlag;}VertexIndexType i;VertexIndexType StartVertexNum      = 0;  //起点个数VertexIndexType EndVertexNum        = 0;  //汇点个数VertexIndexType TmpStartVertexIndex = -1; //起点索引，和StartVertexIndex做对比。VertexIndexType TmpEndVertexIndex   = -1; //汇点索引。for ( i = 0; i < AMG->CurVertexNum; i++){if (AMG->InduityArray[i] == 0){StartVertexNum++;TmpStartVertexIndex = i;}if (StartVertexNum > 1){LogFormat(Debug,"Adjacency Matrix Graph Has Multiple Starting Vertex.\n");return FailFlag;}}if (StartVertexNum != TmpStartVertexIndex){LogFormat(Debug,"StartVertexIndex : %d ,It Has Precursor Vertex, Check Adjacency Matrix Graph Fail\n",StartVertexIndex);}for ( i = 0; i < AMG->CurVertexNum; i++){if (AMG->OutdegreeArray[i] == 0){EndVertexNum++;TmpEndVertexIndex = i;}if (EndVertexNum > 1)//汇点数量大于1，不符合关键路径的场景。{LogFormat(Debug,"Adjacency Matrix Graph Has Multiple Ending Vertex, Check Adjacency Matrix Graph Fail\n");return FailFlag;}}LogFormat(Debug, "(StartVertexIndex : %d,EndVertexIndex : %d), Check Adjacency Matrix Graph OK.\n",TmpStartVertexIndex,TmpEndVertexIndex);return SuccessFlag;
}

8、CheckInduityVertexExists

//检查某个顶点的入度顶点是否都存在于访问哈希表中。
//都被访问过返回：SuccessFlag。反之返回：FailFlag。
Status CheckInduityVertexExists(AMGraph* AMG, VertexIndexType VertexIndex, MyHashTable* VisitedHashTable, SqQueue* VertexEarlyQueue, WeightType* MaxWeight)
{JudgeAllNullPointer(AMG);JudgeAllNullPointer(VisitedHashTable);VertexIndexType i;VertexIndexType Induity         = AMG->InduityArray[VertexIndex];WeightType      PreVertexWeight = 0;//上一个节点的权值if (Induity == 0){LogFormat(Error,"Internal Logic Error, VertexIndex(%d) Induity(0).\n",VertexIndex);return FailFlag;}HashTabElemType HashValue;for (i = 0; i < AMG->CurVertexNum; i++)//入度为复数的情况{if (AMG->ArcArray[i][VertexIndex] != MAX_INT_TYPE_NUM){if (SearchHashTable(VisitedHashTable,&i,&HashValue) == SuccessFlag){ReadSqQueue(VertexEarlyQueue,i,&PreVertexWeight);if (Induity == AMG->InduityArray[VertexIndex])//给MaxWeight赋予初值{*MaxWeight = AMG->ArcArray[i][VertexIndex] + PreVertexWeight;}else{*MaxWeight = MY_MAX(*MaxWeight,AMG->ArcArray[i][VertexIndex] + PreVertexWeight);}Induity--;}else{return FailFlag;}}if (Induity == 0)//说明所有入度点全部被找到，下面的顶点不需要再扫描，跳出循环。{break;}}return SuccessFlag;
}

9、CheckOutDegreeVertexExists

//检查某个顶点的出度顶点是否都存在于访问哈希表中。
//都被访问过返回：SuccessFlag。反之返回：FailFlag。
Status CheckOutDegreeVertexExists(AMGraph* AMG, VertexIndexType VertexIndex, MyHashTable* VisitedHashTable, SqQueue* VertexLateQueue, WeightType* MinWeight)
{JudgeAllNullPointer(AMG);JudgeAllNullPointer(VisitedHashTable);VertexIndexType i;VertexIndexType OutDegree       = AMG->OutdegreeArray[VertexIndex];WeightType      PreVertexWeight = 0;//上一个节点的权值if (OutDegree == 0){LogFormat(Error,"Internal Logic Error, VertexIndex(%d) OutDegree(0).\n",VertexIndex);return FailFlag;}HashTabElemType HashValue;for (i = 0; i < AMG->CurVertexNum; i++)//出度为复数的情况{if (AMG->ArcArray[VertexIndex][i] != MAX_INT_TYPE_NUM){if (SearchHashTable(VisitedHashTable,&i,&HashValue) == SuccessFlag){ReadSqQueue(VertexLateQueue,i,&PreVertexWeight);if (OutDegree == AMG->OutdegreeArray[VertexIndex])//给MinWeight赋予初值{*MinWeight = PreVertexWeight - AMG->ArcArray[VertexIndex][i];}else{*MinWeight = MY_MIN(*MinWeight,PreVertexWeight - AMG->ArcArray[VertexIndex][i]);}OutDegree--;}else{return FailFlag;}}if (OutDegree == 0)//说明所有出度点全部被找到，下面的顶点不需要再扫描，跳出循环。{break;}}return SuccessFlag;
}

10、ComputeCriticalPath

Status ComputeCriticalPath(CriticalPathSt* CP,AMGraph* AMG, VertexIndexType StartVertexIndex)
{JudgeAllNullPointer(CP);JudgeAllNullPointer(AMG);if (CheckCriticalPathAmgIllegal(AMG, StartVertexIndex) == FailFlag){return FailFlag;}ComputeCriticalPathEvent(CP, AMG, StartVertexIndex);ComputeCriticalPathActivity(CP, AMG);LogFormat(Debug, "%s\n", "Compute Critical Path OK.");return SuccessFlag;
}

11、ComputeCriticalPathActivity

Status ComputeCriticalPathActivity(CriticalPathSt* CP,AMGraph* AMG)
{JudgeAllNullPointer(CP);JudgeAllNullPointer(AMG);VertexIndexType i;VertexIndexType j;WeightType      VertexEarlyWeight;WeightType      VertexLateWeight;WeightType      CriticalPathWeight;for (i = 0; i < AMG->CurVertexNum; i++){for (j = 0; j < AMG->CurVertexNum; j++){if (AMG->ArcArray[i][j] != MAX_INT_TYPE_NUM){EnterSqQueue(CP->Activity->ArcStartVertexQueue,&i);EnterSqQueue(CP->Activity->ArcEndVertexQueue,&j);ReadSqQueue(CP->Event->VertexEarlyQueue,i,&VertexEarlyWeight);   EnterSqQueue(CP->Activity->ArcEarlyQueue,&VertexEarlyWeight);ReadSqQueue(CP->Event->VertexLateQueue,j,&VertexLateWeight);VertexLateWeight = VertexLateWeight - AMG->ArcArray[i][j];EnterSqQueue(CP->Activity->ArcLateQueue,&VertexLateWeight);CriticalPathWeight = VertexEarlyWeight - VertexLateWeight;EnterSqQueue(CP->Activity->CriticalPathQueue,&CriticalPathWeight);}}}LogFormat(Debug, "%s\n", "Compute Critical Path Activity OK.");return SuccessFlag;
}

12、ComputeCriticalPathEvent

Status ComputeCriticalPathEvent(CriticalPathSt* CP,AMGraph* AMG, VertexIndexType StartVertexIndex)
{JudgeAllNullPointer(CP);JudgeAllNullPointer(AMG);VertexIndexType InitVal          = CRITICAL_PATH_INIT_VAL;VertexIndexType j;VertexIndexType NextVertexIndex  = StartVertexIndex;//下一个需要访问的顶点行MyHashTable*    VisitedHashTable = NULL;WeightType      TmpWeight        = 0;               //下一个需要访问的顶点的权值WeightType      TmpAddWeight     = 0;               //临时权值和SqStack*        VisitedStack     = NULL;InitSqStack(&VisitedStack,INT_TYPE_FLAG);//1、处理事件最早发生//初始化事件队列for ( j = 0; j < AMG->CurVertexNum; j++){EnterSqQueue(CP->Event->VertexEarlyQueue,&InitVal);EnterSqQueue(CP->Event->VertexLateQueue,&InitVal);}j = 0;UpdateSqQueue(CP->Event->VertexEarlyQueue,StartVertexIndex,&j);//初始化访问数组InitHashTable(&VisitedHashTable, AMG->CurVertexNum, INT_TYPE_FLAG);InsertHashTable(&StartVertexIndex, VisitedHashTable);PushSqStack(VisitedStack,&StartVertexIndex);// PrintfSqQueue(CP->Event->VertexEarlyQueue);// PrintfSqStack(VisitedStack);// PrintfHashTable(VisitedHashTable,Debug);while (VisitedHashTable->TotalDataNum != AMG->CurVertexNum)//所有节点访问一遍，退出循环{PopSqStack(VisitedStack,&NextVertexIndex);ReadSqQueue(CP->Event->VertexEarlyQueue,NextVertexIndex,&TmpWeight);for (j = 0; j < AMG->CurVertexNum; j++)//横向扫描AMG{if (AMG->ArcArray[NextVertexIndex][j] != MAX_INT_TYPE_NUM )//不等于无穷大，说明一定有入度。{if (AMG->InduityArray[j] == 1)//入度为1的情况{InsertHashTable(&j, VisitedHashTable);PushSqStack(VisitedStack,&j);TmpAddWeight   = AMG->ArcArray[NextVertexIndex][j] + TmpWeight;UpdateSqQueue(CP->Event->VertexEarlyQueue,j,&TmpAddWeight);}else if (CheckInduityVertexExists(AMG, j, VisitedHashTable, CP->Event->VertexEarlyQueue, &TmpAddWeight) == SuccessFlag){InsertHashTable(&j, VisitedHashTable);PushSqStack(VisitedStack,&j);UpdateSqQueue(CP->Event->VertexEarlyQueue,j,&TmpAddWeight);}// PrintfSqQueue(CP->Event->VertexEarlyQueue);// PrintfSqStack(VisitedStack);// PrintfHashTable(VisitedHashTable,Debug);}}}//清理访问栈和哈希表ClearSqStack(VisitedStack);ClearHashTable(VisitedHashTable);//2、处理事件最晚发生//和上面时间最早发生的区别是，处理事件最晚是纵向扫描，看顶点的出度，且是从汇点算到起点，倒着算。//初始化for ( j = 0; j < AMG->CurVertexNum; j++){if (AMG->OutdegreeArray[j] == 0)//取汇点索引值。{InitVal = j;break;}}InsertHashTable(&InitVal, VisitedHashTable);PushSqStack(VisitedStack,&InitVal);ReadSqQueue(CP->Event->VertexEarlyQueue,InitVal,&TmpWeight); //读出事件最早发生的汇点权值。UpdateSqQueue(CP->Event->VertexLateQueue,InitVal,&TmpWeight);//更新事件最晚发生的汇点权值。// PrintfSqQueue(CP->Event->VertexLateQueue);// PrintfSqStack(VisitedStack);// PrintfHashTable(VisitedHashTable,Debug);while (VisitedHashTable->TotalDataNum != AMG->CurVertexNum)//所有节点访问一遍，退出循环{PopSqStack(VisitedStack,&NextVertexIndex);ReadSqQueue(CP->Event->VertexLateQueue,NextVertexIndex,&TmpWeight);for (j = 0; j < AMG->CurVertexNum; j++)//纵向扫描AMG{if (AMG->ArcArray[j][NextVertexIndex] != MAX_INT_TYPE_NUM )//不等于无穷大，说明一定有出度。{if (AMG->OutdegreeArray[j] == 1)//出度为1的情况{InsertHashTable(&j, VisitedHashTable);PushSqStack(VisitedStack,&j);TmpAddWeight = TmpWeight - AMG->ArcArray[j][NextVertexIndex];UpdateSqQueue(CP->Event->VertexLateQueue,j,&TmpAddWeight);}else if (CheckOutDegreeVertexExists(AMG, j, VisitedHashTable, CP->Event->VertexLateQueue, &TmpAddWeight) == SuccessFlag){InsertHashTable(&j, VisitedHashTable);PushSqStack(VisitedStack,&j);UpdateSqQueue(CP->Event->VertexLateQueue,j,&TmpAddWeight);}// PrintfSqQueue(CP->Event->VertexLateQueue);// PrintfSqStack(VisitedStack);// PrintfHashTable(VisitedHashTable,Debug);}}}DestroyHashTable(&VisitedHashTable);DestroyStack(&VisitedStack);LogFormat(Debug, "%s\n", "Compute Critical Path Event OK.");return SuccessFlag;
}

十、Linux环境编译测试

[gbase@czg2 Graph]$ make
gcc -Wall -Wextra -O3 Graph.c MinimumSpanningTree.c ShortestPath.c TopologicalOrder.c CriticalPath.c main.c -o TestGraph -I /opt/Developer/ComputerLanguageStudy/C/DataStructureTestSrc/Log/ -I /opt/Developer/ComputerLanguageStudy/C/DataStructureTestSrc/PublicFunction/ -I /opt/Developer/ComputerLanguageStudy/C/DataStructureTestSrc/PublicFunction/HashTable/include/ -I /opt/Developer/ComputerLanguageStudy/C/DataStructureTestSrc/PublicFunction/SqQueue/ -I /opt/Developer/ComputerLanguageStudy/C/DataStructureTestSrc/PublicFunction/SqStack/ -L /opt/Developer/ComputerLanguageStudy/C/DataStructureTestSrc/PublicFunction/Make/Libs/ -lPublicFunction -lLog -lMyHashTable -lSqStack -lSqQueue[gbase@czg2 Graph]$ ./TestGraph 
2023-8-23 16:5:57--[ Debug ]--Create Net Data                    : OK
2023-8-23 16:5:57--[ Debug ]--Create Net Use AMGraph             : OK
2023-8-23 16:5:57--[ Debug ]--Printf AMGraph                     :
VertexArray    : [0 ,1 ,2 ,3 ,4 ,5 ,6 ,7 ,8 ]
ArcArray       :
0  : [32767 ,6     ,4     ,5     ,32767 ,32767 ,32767 ,32767 ,32767 ]
1  : [32767 ,32767 ,32767 ,32767 ,1     ,32767 ,32767 ,32767 ,32767 ]
2  : [32767 ,32767 ,32767 ,32767 ,1     ,32767 ,32767 ,32767 ,32767 ]
3  : [32767 ,32767 ,32767 ,32767 ,32767 ,2     ,32767 ,32767 ,32767 ]
4  : [32767 ,32767 ,32767 ,32767 ,32767 ,32767 ,9     ,7     ,32767 ]
5  : [32767 ,32767 ,32767 ,32767 ,32767 ,32767 ,32767 ,4     ,32767 ]
6  : [32767 ,32767 ,32767 ,32767 ,32767 ,32767 ,32767 ,32767 ,2     ]
7  : [32767 ,32767 ,32767 ,32767 ,32767 ,32767 ,32767 ,32767 ,4     ]
8  : [32767 ,32767 ,32767 ,32767 ,32767 ,32767 ,32767 ,32767 ,32767 ]
InduityArray   : [0 ,1 ,1 ,1 ,2 ,1 ,1 ,2 ,2 ]
OutdegreeArray : [3 ,1 ,1 ,1 ,2 ,1 ,1 ,1 ,0 ]
CurVertexNum   : 9
CurArcNum      : 11
2023-8-23 16:5:57--[ Debug ]--Init SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Init SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Init Critical Path Event St OK.
2023-8-23 16:5:57--[ Debug ]--Init SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Init SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Init SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Init SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Init SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Init Critical Path Activity St OK.
2023-8-23 16:5:57--[ Debug ]--Init Critical Path St OK.
2023-8-23 16:5:57--[ Debug ]--StartVertexIndex : 0 ,It Has Precursor Vertex, Check Adjacency Matrix Graph Fail
2023-8-23 16:5:57--[ Debug ]--(StartVertexIndex : 0,EndVertexIndex : 8), Check Adjacency Matrix Graph OK.
2023-8-23 16:5:57--[ Debug ]--Init SqStack OK.
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Update SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Init Hash Table OK.
2023-8-23 16:5:57--[ Debug ]--Hash : (0,9,0).
2023-8-23 16:5:57--[ Debug ]--New Hash Table Node OK.
2023-8-23 16:5:57--[ Debug ]--Insert Hash Table OK.
2023-8-23 16:5:57--[ Debug ]--Push SqStack OK.
2023-8-23 16:5:57--[ Debug ]--Judge SqStack Not Empty
2023-8-23 16:5:57--[ Debug ]--Pop SqStack OK.
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Hash : (1,9,1).
2023-8-23 16:5:57--[ Debug ]--New Hash Table Node OK.
2023-8-23 16:5:57--[ Debug ]--Insert Hash Table OK.
2023-8-23 16:5:57--[ Debug ]--Push SqStack OK.
2023-8-23 16:5:57--[ Debug ]--Update SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Hash : (2,9,2).
2023-8-23 16:5:57--[ Debug ]--New Hash Table Node OK.
2023-8-23 16:5:57--[ Debug ]--Insert Hash Table OK.
2023-8-23 16:5:57--[ Debug ]--Push SqStack OK.
2023-8-23 16:5:57--[ Debug ]--Update SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Hash : (3,9,3).
2023-8-23 16:5:57--[ Debug ]--New Hash Table Node OK.
2023-8-23 16:5:57--[ Debug ]--Insert Hash Table OK.
2023-8-23 16:5:57--[ Debug ]--Push SqStack OK.
2023-8-23 16:5:57--[ Debug ]--Update SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Judge SqStack Not Empty
2023-8-23 16:5:57--[ Debug ]--Pop SqStack OK.
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Hash : (5,9,5).
2023-8-23 16:5:57--[ Debug ]--New Hash Table Node OK.
2023-8-23 16:5:57--[ Debug ]--Insert Hash Table OK.
2023-8-23 16:5:57--[ Debug ]--Push SqStack OK.
2023-8-23 16:5:57--[ Debug ]--Update SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Judge SqStack Not Empty
2023-8-23 16:5:57--[ Debug ]--Pop SqStack OK.
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Hash : (4,9,4).
2023-8-23 16:5:57--[ Debug ]--Search Hash Table Fail, HashValue : 4.
2023-8-23 16:5:57--[ Debug ]--Judge SqStack Not Empty
2023-8-23 16:5:57--[ Debug ]--Pop SqStack OK.
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Hash : (1,9,1).
2023-8-23 16:5:57--[ Debug ]--Search Hash Table OK, HashValue : 1.
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Hash : (2,9,2).
2023-8-23 16:5:57--[ Debug ]--Search Hash Table OK, HashValue : 2.
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Hash : (4,9,4).
2023-8-23 16:5:57--[ Debug ]--New Hash Table Node OK.
2023-8-23 16:5:57--[ Debug ]--Insert Hash Table OK.
2023-8-23 16:5:57--[ Debug ]--Push SqStack OK.
2023-8-23 16:5:57--[ Debug ]--Update SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Judge SqStack Not Empty
2023-8-23 16:5:57--[ Debug ]--Pop SqStack OK.
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Hash : (6,9,6).
2023-8-23 16:5:57--[ Debug ]--New Hash Table Node OK.
2023-8-23 16:5:57--[ Debug ]--Insert Hash Table OK.
2023-8-23 16:5:57--[ Debug ]--Push SqStack OK.
2023-8-23 16:5:57--[ Debug ]--Update SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Hash : (4,9,4).
2023-8-23 16:5:57--[ Debug ]--Search Hash Table OK, HashValue : 4.
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Hash : (5,9,5).
2023-8-23 16:5:57--[ Debug ]--Search Hash Table OK, HashValue : 5.
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Hash : (7,9,7).
2023-8-23 16:5:57--[ Debug ]--New Hash Table Node OK.
2023-8-23 16:5:57--[ Debug ]--Insert Hash Table OK.
2023-8-23 16:5:57--[ Debug ]--Push SqStack OK.
2023-8-23 16:5:57--[ Debug ]--Update SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Judge SqStack Not Empty
2023-8-23 16:5:57--[ Debug ]--Pop SqStack OK.
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Hash : (6,9,6).
2023-8-23 16:5:57--[ Debug ]--Search Hash Table OK, HashValue : 6.
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Hash : (7,9,7).
2023-8-23 16:5:57--[ Debug ]--Search Hash Table OK, HashValue : 7.
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Hash : (8,9,8).
2023-8-23 16:5:57--[ Debug ]--New Hash Table Node OK.
2023-8-23 16:5:57--[ Debug ]--Insert Hash Table OK.
2023-8-23 16:5:57--[ Debug ]--Push SqStack OK.
2023-8-23 16:5:57--[ Debug ]--Update SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Clear SqStack OK.
2023-8-23 16:5:57--[ Debug ]--Clear Hash Table OK.
2023-8-23 16:5:57--[ Debug ]--Hash : (8,9,8).
2023-8-23 16:5:57--[ Debug ]--New Hash Table Node OK.
2023-8-23 16:5:57--[ Debug ]--Insert Hash Table OK.
2023-8-23 16:5:57--[ Debug ]--Push SqStack OK.
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Update SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Judge SqStack Not Empty
2023-8-23 16:5:57--[ Debug ]--Pop SqStack OK.
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Hash : (6,9,6).
2023-8-23 16:5:57--[ Debug ]--New Hash Table Node OK.
2023-8-23 16:5:57--[ Debug ]--Insert Hash Table OK.
2023-8-23 16:5:57--[ Debug ]--Push SqStack OK.
2023-8-23 16:5:57--[ Debug ]--Update SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Hash : (7,9,7).
2023-8-23 16:5:57--[ Debug ]--New Hash Table Node OK.
2023-8-23 16:5:57--[ Debug ]--Insert Hash Table OK.
2023-8-23 16:5:57--[ Debug ]--Push SqStack OK.
2023-8-23 16:5:57--[ Debug ]--Update SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Judge SqStack Not Empty
2023-8-23 16:5:57--[ Debug ]--Pop SqStack OK.
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Hash : (6,9,6).
2023-8-23 16:5:57--[ Debug ]--Search Hash Table OK, HashValue : 6.
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Hash : (7,9,7).
2023-8-23 16:5:57--[ Debug ]--Search Hash Table OK, HashValue : 7.
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Hash : (4,9,4).
2023-8-23 16:5:57--[ Debug ]--New Hash Table Node OK.
2023-8-23 16:5:57--[ Debug ]--Insert Hash Table OK.
2023-8-23 16:5:57--[ Debug ]--Push SqStack OK.
2023-8-23 16:5:57--[ Debug ]--Update SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Hash : (5,9,5).
2023-8-23 16:5:57--[ Debug ]--New Hash Table Node OK.
2023-8-23 16:5:57--[ Debug ]--Insert Hash Table OK.
2023-8-23 16:5:57--[ Debug ]--Push SqStack OK.
2023-8-23 16:5:57--[ Debug ]--Update SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Judge SqStack Not Empty
2023-8-23 16:5:57--[ Debug ]--Pop SqStack OK.
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Hash : (3,9,3).
2023-8-23 16:5:57--[ Debug ]--New Hash Table Node OK.
2023-8-23 16:5:57--[ Debug ]--Insert Hash Table OK.
2023-8-23 16:5:57--[ Debug ]--Push SqStack OK.
2023-8-23 16:5:57--[ Debug ]--Update SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Judge SqStack Not Empty
2023-8-23 16:5:57--[ Debug ]--Pop SqStack OK.
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Hash : (1,9,1).
2023-8-23 16:5:57--[ Debug ]--Search Hash Table Fail, HashValue : 1.
2023-8-23 16:5:57--[ Debug ]--Judge SqStack Not Empty
2023-8-23 16:5:57--[ Debug ]--Pop SqStack OK.
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Hash : (1,9,1).
2023-8-23 16:5:57--[ Debug ]--New Hash Table Node OK.
2023-8-23 16:5:57--[ Debug ]--Insert Hash Table OK.
2023-8-23 16:5:57--[ Debug ]--Push SqStack OK.
2023-8-23 16:5:57--[ Debug ]--Update SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Hash : (2,9,2).
2023-8-23 16:5:57--[ Debug ]--New Hash Table Node OK.
2023-8-23 16:5:57--[ Debug ]--Insert Hash Table OK.
2023-8-23 16:5:57--[ Debug ]--Push SqStack OK.
2023-8-23 16:5:57--[ Debug ]--Update SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Judge SqStack Not Empty
2023-8-23 16:5:57--[ Debug ]--Pop SqStack OK.
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Hash : (1,9,1).
2023-8-23 16:5:57--[ Debug ]--Search Hash Table OK, HashValue : 1.
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Hash : (2,9,2).
2023-8-23 16:5:57--[ Debug ]--Search Hash Table OK, HashValue : 2.
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Hash : (3,9,3).
2023-8-23 16:5:57--[ Debug ]--Search Hash Table OK, HashValue : 3.
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Hash : (0,9,0).
2023-8-23 16:5:57--[ Debug ]--New Hash Table Node OK.
2023-8-23 16:5:57--[ Debug ]--Insert Hash Table OK.
2023-8-23 16:5:57--[ Debug ]--Push SqStack OK.
2023-8-23 16:5:57--[ Debug ]--Update SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Clear Hash Table OK.
2023-8-23 16:5:57--[ Debug ]--Destroy Hash Table OK.
2023-8-23 16:5:57--[ Debug ]--Destroy SqStack OK.
2023-8-23 16:5:57--[ Debug ]--Compute Critical Path Event OK.
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Read  SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Enter SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Compute Critical Path Activity OK.
2023-8-23 16:5:57--[ Debug ]--Compute Critical Path OK.
2023-8-23 16:5:57--[ Debug ]--SqQueue Data   :
Data           : [ 0 ,6 ,4 ,5 ,7 ,7 ,16 ,14 ,18 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 9
SqQueueMaxLen  : 9
Flag           : INT_TYPE_FLAG
2023-8-23 16:5:57--[ Debug ]--SqQueue Data   :
Data           : [ 0 ,6 ,6 ,8 ,7 ,10 ,16 ,14 ,18 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 9
SqQueueMaxLen  : 9
Flag           : INT_TYPE_FLAG
2023-8-23 16:5:57--[ Debug ]--SqQueue Data   :
Data           : [ 0 ,0 ,0 ,1 ,2 ,3 ,4 ,4 ,5 ,6 ,7 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 11
SqQueueMaxLen  : 11
Flag           : INT_TYPE_FLAG
2023-8-23 16:5:57--[ Debug ]--SqQueue Data   :
Data           : [ 1 ,2 ,3 ,4 ,4 ,5 ,6 ,7 ,7 ,8 ,8 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 11
SqQueueMaxLen  : 11
Flag           : INT_TYPE_FLAG
2023-8-23 16:5:57--[ Debug ]--SqQueue Data   :
Data           : [ 0 ,0 ,0 ,6 ,4 ,5 ,7 ,7 ,7 ,16 ,14 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 11
SqQueueMaxLen  : 11
Flag           : INT_TYPE_FLAG
2023-8-23 16:5:57--[ Debug ]--SqQueue Data   :
Data           : [ 0 ,2 ,3 ,6 ,6 ,8 ,7 ,7 ,10 ,16 ,14 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 11
SqQueueMaxLen  : 11
Flag           : INT_TYPE_FLAG
2023-8-23 16:5:57--[ Debug ]--SqQueue Data   :
Data           : [ 0 ,-2 ,-3 ,0 ,-2 ,-3 ,0 ,0 ,-3 ,0 ,0 ]
FrontIndex     : 0
RearIndex      : 0
SqQueueLen     : 11
SqQueueMaxLen  : 11
Flag           : INT_TYPE_FLAG
2023-8-23 16:5:57--[ Debug ]--Destroy SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Destroy SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Destroy Critical Path Event St OK.
2023-8-23 16:5:57--[ Debug ]--Destroy SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Destroy SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Destroy SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Destroy SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Destroy SqQueue OK
2023-8-23 16:5:57--[ Debug ]--Destroy Critical Path Activity St OK.
2023-8-23 16:5:57--[ Debug ]--Destroy Critical Path St OK.
2023-8-23 16:5:57--[ Debug ]--Destroy SqStack OK.
2023-8-23 16:5:57--[ Debug ]--Destroy StAccessPath OK.
2023-8-23 16:5:57--[ Debug ]--Destroy StAccessPath OK.
2023-8-23 16:5:57--[ Debug ]--Destroy StAccessPath OK.
2023-8-23 16:5:57--[ Debug ]--Destroy StAccessPath OK.
2023-8-23 16:5:57--[ Debug ]--Destroy StAccessPath OK.
2023-8-23 16:5:57--[ Debug ]--Destroy StAccessPath OK.
2023-8-23 16:5:57--[ Debug ]--Destroy StAccessPath OK.
2023-8-23 16:5:57--[ Debug ]--Destroy StAccessPath OK.
2023-8-23 16:5:57--[ Debug ]--Destroy StDijkstraAccees OK.
2023-8-23 16:5:57--[ Debug ]--Destroy Net Data                   : OK
2023-8-23 16:5:57--[ Debug ]--Destroy Net Use AMGraph            : OK
2023-8-23 16:5:57--[ Debug ]--Destroy Net Use AGraph             : OK

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/102833.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

自带云盘的内网即时通讯软件，保障数据在公司局域网内安全流通

自带云盘的内网即时通讯软件，保障数据在公司局域网内安全流通

在信息时代&#xff0c;很多对于内部机密性要求较高的企业&#xff0c;都不惜成本地选择在内网搭建专属的私有化即时通讯系统。企业员工在内部通讯与协同办公的时候&#xff0c;会分享一些文件、文档等资料&#xff0c; 为了保证所有在通讯软件流通的文件&#xff0c;就需要选…
阅读更多...
Sui第四轮资助：16个团队瓜分

Sui第四轮资助：16个团队瓜分

近日&#xff0c;Sui基金会公布了第四轮开发者资助名单&#xff0c;受助项目均是集中在DeFi、支付、基础设施、游戏、预言机等领域的Sui生态项目&#xff0c;他们是从2023年7月1日之前提交的申请中选出的。在此时间之后提交的任何项目目前正在审查中。 在前三轮资助中累积发放…
阅读更多...
视频转音频mp3怎么弄？

视频转音频mp3怎么弄？

视频转音频mp3怎么弄&#xff1f;在很多人看来&#xff0c;音频就是视频中的一部分&#xff0c;其实这时是一定道理的&#xff0c;视频是一种包含图像和有声音的多媒体文件&#xff0c;没有声音的视频是不完美的。时代发展到现在&#xff0c;短视频已经融入了我们生活的方方面面…
阅读更多...
百度许少辉著Baidu《乡村振兴战略下传统村落文化旅游设计》图书馆新书通报

百度许少辉著Baidu《乡村振兴战略下传统村落文化旅游设计》图书馆新书通报

百度许少辉著Baidu《乡村振兴战略下传统村落文化旅游设计》图书馆新书通报
阅读更多...
什么是变量提升（hoisting）？它在JavaScript中是如何工作的？

什么是变量提升（hoisting）？它在JavaScript中是如何工作的？

聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 变量提升&#xff08;Hoisting&#xff09;⭐ 变量提升的示例&#xff1a;⭐ 写在最后 ⭐ 专栏简介 前端入门之旅&#xff1a;探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦 几何带你启航前端之旅 欢迎来到前端入门之旅&…
阅读更多...
微服务架构2.0--云原生时代

微服务架构2.0--云原生时代

云原生 云原生&#xff08;Cloud Native&#xff09;是一种关注于在云环境中构建、部署和管理应用程序的方法和理念。云原生应用能够最大程度地利用云计算基础设施的优势&#xff0c;如弹性、自动化、可伸缩性和高可用性。这个概念涵盖了许多方面&#xff0c;包括架构、开发、…
阅读更多...
【FAQ】H.265视频无插件流媒体播放器EasyPlayer.js播放webrtc断流重连的异常修复

【FAQ】H.265视频无插件流媒体播放器EasyPlayer.js播放webrtc断流重连的异常修复

H5无插件流媒体播放器EasyPlayer属于一款高效、精炼、稳定且免费的流媒体播放器&#xff0c;可支持多种流媒体协议播放&#xff0c;可支持H.264与H.265编码格式&#xff0c;性能稳定、播放流畅&#xff0c;能支持WebSocket-FLV、HTTP-FLV&#xff0c;HLS&#xff08;m3u8&#…
阅读更多...
ssm网上医院预约挂号系统源码和论文

ssm网上医院预约挂号系统源码和论文

ssm网上医院预约挂号系统源码和论文051 开发工具&#xff1a;idea 数据库mysql5.7 数据库链接工具&#xff1a;navcat,小海豚等 技术&#xff1a;ssm 摘 要 如今的信息时代&#xff0c;对信息的共享性&#xff0c;信息的流通性有着较高要求&#xff0c;因此传统管理方式…
阅读更多...
数据结构初阶--排序

数据结构初阶--排序

目录 一.排序的基本概念 1.1.什么是排序 1.2.排序算法的评价指标 1.3.排序的分类 二.插入排序 2.1.直接插入排序 2.2.希尔排序 三.选择排序 3.1.直接选择排序 3.2.堆排序 重建堆 建堆 排序 四.交换排序 4.1.冒泡排序 4.2.快速排序 快速排序的递归实现 法一&a…
阅读更多...
【每日易题】七夕限定——单身狗问题以及进阶问题位运算法的深入探讨

【每日易题】七夕限定——单身狗问题以及进阶问题位运算法的深入探讨

君兮_的个人主页 勤时当勉励 岁月不待人 C/C 游戏开发 Hello,米娜桑们&#xff0c;这里是君兮_&#xff0c;在写这篇博客的前一天是七夕&#xff0c;也是中国传统的“情人节”&#xff0c;不知道各位脱单了吗&#xff1f;碰巧最近刷题时遇到了经典的单身狗问题想带大家深入探…
阅读更多...
设计模式概述

设计模式概述

文章目录 设计模式概述创建型模式&#xff1a;结构型模式&#xff1a;行为型模式&#xff1a; 设计模式概述 设计模式是什么&#xff1f; 设计模式的一般定义为&#xff1a; 设计模式&#xff08;Design Pattern&#xff09;是一套反复使用、多人知晓的&#xff0c;经过分类…
阅读更多...
java电子病历源码 电子病历编辑器源码 病历在线制作、管理和使用

java电子病历源码 电子病历编辑器源码 病历在线制作、管理和使用

电子病历在线制作、管理和使用的一体化电子病历解决方案&#xff0c;通过一体化的设计&#xff0c;提供对住院病人的电子病历书写、保存、修改、打印等功能。电子病历系统将临床医护需要的诊疗资料以符合临床思维的方法展示。建立以病人为中心&#xff0c;以临床诊疗信息为主线…
阅读更多...
echart 图表添加数据分析功能,(右上控制选择)

echart 图表添加数据分析功能,(右上控制选择)

echart 图表添加数据分析功能,可区域选择数据,右上按钮,控制echart行为 chart.on(globalcursortaken, onGlobalcursortaken); //绑定事件chart.off("brushSelected");//解绑事件处理函数chart.on(brushSelected, renderBrushed);getBarDev2(eIndex, eTimeArr, eSerie…
阅读更多...
mmdetection基于 PyTorch 的目标检测开源工具箱 入门教程

mmdetection基于 PyTorch 的目标检测开源工具箱 入门教程

安装环境 MMDetection 支持在 Linux&#xff0c;Windows 和 macOS 上运行。它需要 Python 3.7 以上&#xff0c;CUDA 9.2 以上和 PyTorch 1.8 及其以上。 1、安装依赖 步骤 0. 从官方网站下载并安装 Miniconda。 步骤 1. 创建并激活一个 conda 环境。 conda create --name…
阅读更多...
Java 中使用 ES 高级客户端库 RestHighLevelClient 清理百万级规模历史数据

Java 中使用 ES 高级客户端库 RestHighLevelClient 清理百万级规模历史数据

&#x1f389;工作中遇到这样一个需求场景&#xff1a;由于ES数据库中历史数据过多&#xff0c;占用太多的磁盘空间&#xff0c;需要定期地进行清理&#xff0c;在一定程度上可以释放磁盘空间&#xff0c;减轻磁盘空间压力。 &#x1f388;在经过调研之后发现&#xff0c;某服务…
阅读更多...
SpringCloud学习笔记(四)_ZooKeeper注册中心

SpringCloud学习笔记(四)_ZooKeeper注册中心

基于Spring Cloud实现服务的发布与调用。而在18年7月份&#xff0c;Eureka2.0宣布停更了&#xff0c;将不再进行开发&#xff0c;所以对于公司技术选型来说&#xff0c;可能会换用其他方案做注册中心。本章学习便是使用ZooKeeper作为注册中心。 本章使用的zookeeper版本是 3.6…
阅读更多...
vue中form和table标签过长

vue中form和table标签过长

form标签过长 效果&#xff1a; 代码&#xff1a; <el-form-item v-for"(item,index) in ticketEditTable1" :label"item.fieldNameCn" :propitem.fieldName :key"item.fieldNameCn" overflow"":rules"form[item.fieldName…
阅读更多...
【Unity】Text文本组件的一些操作

【Unity】Text文本组件的一些操作

Unity的Text组件的几种常见的操作方法 Text组件是Unity中用于在UI界面上显示文本的组件。它包含了一些常见的属性和方法&#xff0c;可以用来控制文本的内容、外观和交互。以下是一些常见的Text组件的操作&#xff1a; 设置文本内容&#xff1a;通过直接在Unity编辑器中的Text…
阅读更多...
【方案】基于AI边缘计算的智慧工地解决方案

【方案】基于AI边缘计算的智慧工地解决方案

一、方案背景 在工程项目管理中&#xff0c;工程施工现场涉及面广&#xff0c;多种元素交叉&#xff0c;状况较为复杂&#xff0c;如人员出入、机械运行、物料运输等。特别是传统的现场管理模式依赖于管理人员的现场巡查。当发现安全风险时&#xff0c;需要提前报告&#xff0…
阅读更多...
C语言基础之——操作符（上）

C语言基础之——操作符（上）

本篇文章&#xff0c;我们将展开讲解C语言中的各种常用操作符&#xff0c;帮助大家更容易的解决一些运算类问题。 这里提醒一下小伙伴们&#xff0c;本章知识会大量涉及到二进制序列&#xff0c;不清楚二进制序列的小伙伴&#xff0c;可以去阅读我的另一篇文章《数据在内存中的…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023