目录
- 题目:辗转相除法(求最大公约数)
- 思路分析:辗转相除法(也叫欧几里得算法)`gcd(a,b) = gcd(b,a mod b)`
- 复杂度:时间复杂度 O ( n + l o g ( m a x ) ) O(n+log(max)) O(n+log(max))、空间复杂度 O ( 1 ) O(1) O(1)
- Go代码
- 题目:判断是否是素数
- 思路分析:判断n是否是素数只需测试 2 到 sqrtN 的所有可能因子 + "6K +1/-1" 规则
- 复杂度:时间复杂度 O ( s q r t ( n ) ) O(sqrt(n)) O(sqrt(n))、空间复杂度 O ( 1 ) O(1) O(1)
- Go代码
- 题目:埃氏筛
- 思路分析:埃氏筛法思想,逐步排除掉不是质数的数
- 复杂度:时间复杂度 O ( n l o g l o g n ) O(n log log n) O(nloglogn)、空间复杂度 O ( n ) O(n) O(n)
- Go代码
- 题目:判断是不是丑数
- 思路分析:循环除2 3 5 判断最后值是否==1
- 复杂度:时间复杂度 O ( l o g n ) O(log n) O(logn)、空间复杂度 O ( 1 ) O(1) O(1)
- Go代码
题目:辗转相除法(求最大公约数)
题目链接:LeetCode-1979. 找出数组的最大公约数

思路分析:辗转相除法(也叫欧几里得算法)gcd(a,b) = gcd(b,a mod b)
辗转相除法其核心部分为:若r 是a ÷ b的余数,则 gcd(a, b)=gcd(b, r)
复杂度:时间复杂度 O ( n + l o g ( m a x ) ) O(n+log(max)) O(n+log(max))、空间复杂度 O ( 1 ) O(1) O(1)
Go代码
func findGCD(nums []int) int {max, min := getMaxMin(nums)return getGcd(max, min)
}
// gcd求最大公约数
func getGcd(a int, b int) int {yu := 0for b != 0 {yu = a % b //得到余数a = b //根据辗转相除法,把被除数赋给除数b = yu //余数赋给被除数}return a //返回除数
}
func getMaxMin(nums []int) (max int, min int) {max, min = nums[0], nums[0]length := len(nums)for i:=1; i<length; i++ {if nums[i] > max {max = nums[i]}if nums[i] < min {min = nums[i]}}return
}
题目:判断是否是素数
思路分析:判断n是否是素数只需测试 2 到 sqrtN 的所有可能因子 + “6K +1/-1” 规则
复杂度:时间复杂度 O ( s q r t ( n ) ) O(sqrt(n)) O(sqrt(n))、空间复杂度 O ( 1 ) O(1) O(1)
Go代码
func isPrimes(n int) bool {if n <= 1 {return false}if n <= 3 {return true}if n%2==0 || n%3==0 {return false}// 判断n是否是素数时,只需要测试 2 到 sqrtN 的所有可能因子// max := int(math.Pow(float64(n), 0.5))max := int(math.Sqrt(float64(n)))// 根据 "6K +1/-1" 规则for i:=5; i<=max; i+=6 {// i+2 正好是 "6K +1/-1" 中的一个值if n % i == 0 || n%(i+2) == 0 {return false}}return true
}
题目:埃氏筛
题目链接:LeetCode-204. 计数质数

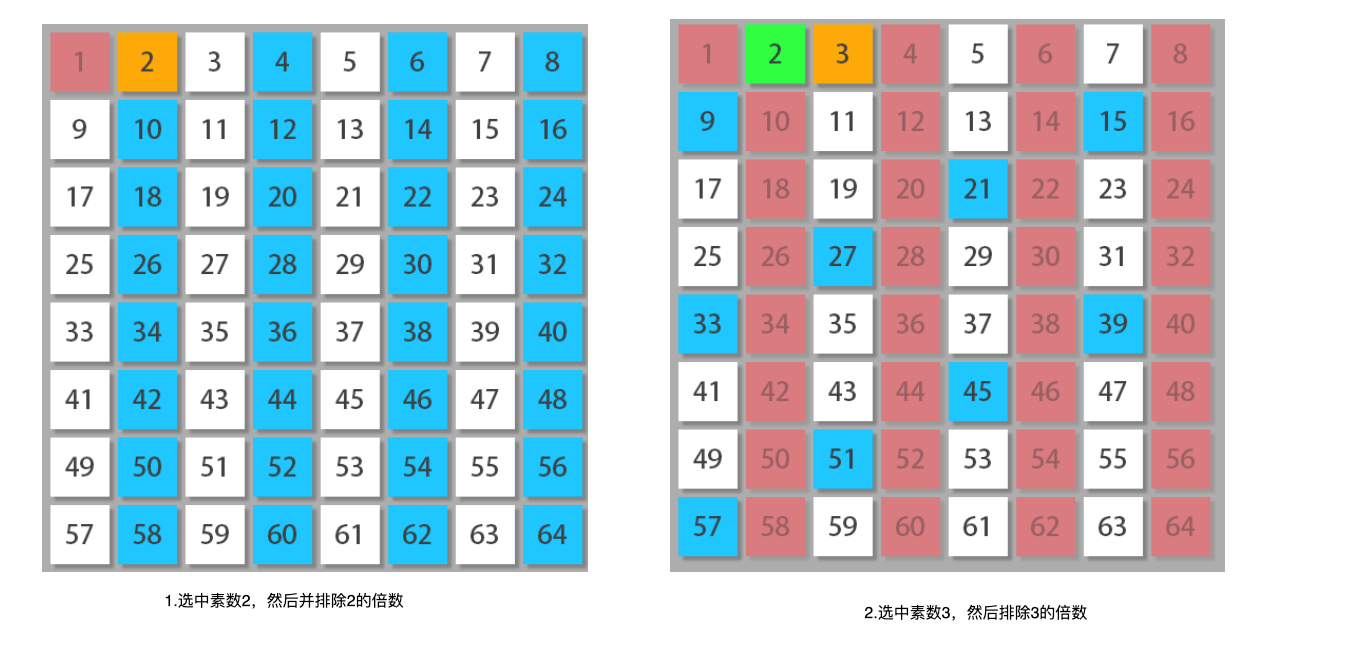
思路分析:埃氏筛法思想,逐步排除掉不是质数的数
如果 x 是质数,那么大于 x 的 x 的倍数 2x,3x,… 一定不是质数。
复杂度:时间复杂度 O ( n l o g l o g n ) O(n log log n) O(nloglogn)、空间复杂度 O ( n ) O(n) O(n)
- 时间复杂度分析:
- 外层循环的迭代次数是 n-2,即 O ( n ) O(n) O(n) 次。
- 内层循环的迭代次数是在素数的情况下,从 i*i 开始,每次递增 i,直到 n。这是因为小于 i 的倍数在之前已经被标记为非质数。内层循环迭代次数约为 n/i,其中 i 为质数。因此,总的迭代次数为 n/2 + n/3 + n/5 + …,这个和式是 O ( n l o g l o g n ) O(n log log n) O(nloglogn)的。
Go代码
func countPrimes(n int) int {count := 0isNotPrimes := make([]bool, n)for i:=2; i<n; i++ {if !isNotPrimes[i] {count++for j:=i*i; j<n; j+=i {isNotPrimes[j] = true}}}return count
}
或者 下面这个语言更清晰,不过多了 O ( n ) O(n) O(n)的时间复杂度
func countPrimes(n int) (count int) {isPrimies := make([]bool, n)for i, _ := range isPrimies {isPrimies[i] = true}for i:=2; i<n; i++ {// 从2开始已经把2的所有倍数标记为false,3也是,所以剩下的未标记的都是质数if isPrimies[i] {count++// 直接从i*i开始标记,因为2i,3i...这些数一定在i之前就被其他数的倍数标记过了,例如2的所有倍数,3的所有倍数等for j:=i*i; j<n; j+=i {isPrimies[j] = false}}}return
}
题目:判断是不是丑数
题目链接:LeetCode-263. 丑数

思路分析:循环除2 3 5 判断最后值是否==1
复杂度:时间复杂度 O ( l o g n ) O(log n) O(logn)、空间复杂度 O ( 1 ) O(1) O(1)
- 时间复杂度:取决于对n除以2 3 5的次数,由于每次至少将n除以2,所以除法运算的次数不会超过 O ( l o g n ) O(log n) O(logn)
Go代码
func isUgly(n int) bool {if n < 1 {return false}if n == 1 {return true}arr := [3]int{2,3,5}for _, v := range arr {for n%v == 0 {n = n/v}}return n == 1
}