机器学习笔记之优化算法——梯度下降法在强凸函数上的收敛性证明
- 引言
- 回顾:
- 凸函数与强凸函数
- 梯度下降法:凸函数上的收敛性分析
- 关于白老爹定理的一些新的认识
- 梯度下降法在强凸函数上的收敛性
- 收敛性定理介绍
- 结论分析
- 证明过程
引言
本节将介绍:梯度下降法在强凸函数上的收敛性,以及证明过程。
回顾:
凸函数与强凸函数
关于凸函数的定义使用数学符号表示如下:
∀ x 1 , x 2 ∈ R n , ∀ λ ∈ ( 0 , 1 ) ⇒ f [ λ ⋅ x 2 + ( 1 − λ ) ⋅ x 1 ] ≤ λ ⋅ f ( x 2 ) + ( 1 − λ ) ⋅ f ( x 1 ) \forall x_1,x_2 \in \mathbb R^n, \forall \lambda \in (0,1) \Rightarrow f [\lambda \cdot x_2 + (1 - \lambda) \cdot x_1] \leq \lambda \cdot f(x_2) + (1 - \lambda) \cdot f(x_1) ∀x1,x2∈Rn,∀λ∈(0,1)⇒f[λ⋅x2+(1−λ)⋅x1]≤λ⋅f(x2)+(1−λ)⋅f(x1)
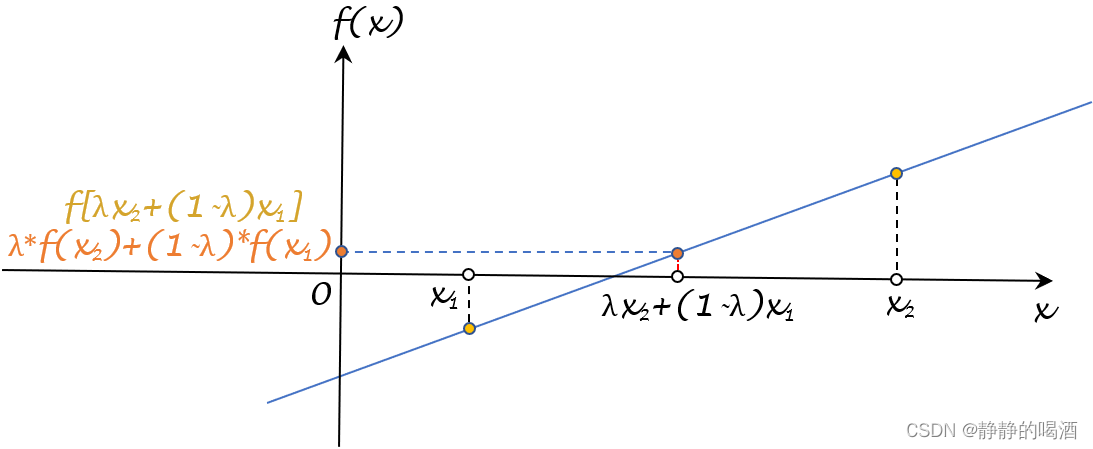
很明显,这描述的是 f [ λ ⋅ x 2 + ( 1 − λ ) ⋅ x 1 ] f[\lambda \cdot x_2 + (1 - \lambda) \cdot x_1] f[λ⋅x2+(1−λ)⋅x1]与 λ ⋅ f ( x 2 ) + ( 1 − λ ) ⋅ f ( x 1 ) \lambda \cdot f(x_2) + (1 - \lambda) \cdot f(x_1) λ⋅f(x2)+(1−λ)⋅f(x1)两个量之间的大小关系。以 x 1 , x 2 ∈ R x_1,x_2 \in \mathbb R x1,x2∈R为例,它们的大小关系在图像中表示如下:

观察公式,可以看出:作为凸函数的定义,两个量之间有机会取等。依然以 x 1 , x 2 ∈ R x_1,x_2 \in \mathbb R x1,x2∈R为例,两个量取等情况下的图像示例如下:
很明显,这是一个线性函数,对应的函数图像是一条直线。任选 x 1 , x 2 ∈ R x_1,x_2 \in \mathbb R x1,x2∈R,对应函数结果的连线内的任意一点都在该直线上。
类似地,关于强凸函数的定义使用数学符号表示如下:对于 ∀ x 1 , x 2 ∈ R n , ∀ λ ∈ ( 0 , 1 ) , ∃ m > 0 \forall x_1,x_2 \in \mathbb R^n,\forall \lambda \in (0,1),\exist m > 0 ∀x1,x2∈Rn,∀λ∈(0,1),∃m>0,总有:
λ ⋅ f ( x 1 ) + ( 1 − λ ) ⋅ f ( x 2 ) ≥ f [ λ ⋅ x 1 + ( 1 − λ ) ⋅ x 2 ] + m 2 ⋅ λ ( 1 − λ ) ⋅ ∣ ∣ x 1 − x 2 ∣ ∣ 2 \lambda \cdot f(x_1) + (1 - \lambda) \cdot f(x_2) \geq f[\lambda \cdot x_1 + (1 - \lambda) \cdot x_2] + \frac{m}{2} \cdot \lambda(1 - \lambda) \cdot ||x_1 - x_2||^2 λ⋅f(x1)+(1−λ)⋅f(x2)≥f[λ⋅x1+(1−λ)⋅x2]+2m⋅λ(1−λ)⋅∣∣x1−x2∣∣2
相比于凸函数的定义,强凸函数定义明显的特点是:两个量之间不仅不能取等,并且还要相差一个大小为 m 2 ⋅ λ ( 1 − λ ) ⋅ ∣ ∣ x 1 − x 2 ∣ ∣ 2 \begin{aligned}\frac{m}{2} \cdot \lambda(1 - \lambda) \cdot ||x_1 - x_2||^2\end{aligned} 2m⋅λ(1−λ)⋅∣∣x1−x2∣∣2的正值。
其中m m m表示描述强凸函数的参数,也被称作m m m-强凸函数。这种定义的描述彻底杜绝了线性函数这种‘看起来不凸’的凸函数的情况。也就是说,强凸函数对于两个量之间的大小关系的约束更强了。
梯度下降法:凸函数上的收敛性分析
关于梯度下降法在凸函数上的收敛性描述表示如下:
- 条件:
- 函数 f ( ⋅ ) f(\cdot) f(⋅)向下有界,在其定义域内可微,并且 f ( ⋅ ) f(\cdot) f(⋅)是凸函数;
- 关于梯度函数 ∇ f ( ⋅ ) \nabla f(\cdot) ∇f(⋅)满足 L \mathcal L L-利普希兹连续;
- 在梯度下降法的迭代过程中,步长 α k ( k = 1 , 2 , 3 , ⋯ ) \alpha_k(k=1,2,3,\cdots) αk(k=1,2,3,⋯)存在明确的约束范围: α k ∈ ( 0 , 1 L ] \begin{aligned}\alpha_k \in \left(0,\frac{1}{\mathcal L}\right]\end{aligned} αk∈(0,L1];
关于步长α k \alpha_k αk约束范围的上界1 L \begin{aligned}\frac{1}{\mathcal L}\end{aligned} L1,详见二次上界引理,这里不再赘述。
- 结论:目标函数序列 { f ( x k ) } k = 0 ∞ \{f(x_k)\}_{k=0}^{\infty} {f(xk)}k=0∞以 O ( 1 k ) \begin{aligned}\mathcal O \left(\frac{1}{k}\right)\end{aligned} O(k1)的收敛类型,次线性收敛于目标函数的最优解 f ∗ f^* f∗。
关于证明过程详见优化算法——梯度下降法在凸函数上的收敛性
关于白老爹定理的一些新的认识
在 Baillon Haddad Theorem \text{Baillon Haddad Theorem} Baillon Haddad Theorem一节中介绍过:如果 f ( ⋅ ) f(\cdot) f(⋅)在定义域内可微,并且是凸函数,而且 ∇ f ( ⋅ ) \nabla f(\cdot) ∇f(⋅)满足 L \mathcal L L-利普希兹连续,那么必然有:函数 G ( x ) = L 2 x T x − f ( x ) \begin{aligned}\mathcal G(x) = \frac{\mathcal L}{2}x^Tx - f(x)\end{aligned} G(x)=2LxTx−f(x)同样是凸函数。
虽然证明过程比较简单,但新的问题出现:为什么要设计 G ( x ) \mathcal G(x) G(x)这样的函数 ? ? ?或者关于项 L 2 x T x \begin{aligned}\frac{\mathcal L}{2}x^Tx\end{aligned} 2LxTx产生的原因是什么 ? ? ?是否存在什么意义 ? ? ?
重新观察: ∇ f ( ⋅ ) \nabla f(\cdot) ∇f(⋅)满足 L \mathcal L L-利普希兹连续这个条件:
∀ x , y ∈ R n , ∃ L ⇒ ∣ ∣ ∇ f ( x ) − ∇ f ( y ) ∣ ∣ ≤ L ⋅ ∣ ∣ x − y ∣ ∣ \forall x,y \in \mathbb R^n,\exist \mathcal L \Rightarrow ||\nabla f(x) - \nabla f(y)|| \leq \mathcal L \cdot ||x - y|| ∀x,y∈Rn,∃L⇒∣∣∇f(x)−∇f(y)∣∣≤L⋅∣∣x−y∣∣
如果函数 f ( ⋅ ) f(\cdot) f(⋅)在其定义域内二阶可微,根据拉格朗日中值定理,有:
其中 I \mathcal I I表示单位矩阵。
∃ ξ ∈ ( x , y ) ⇒ ∣ ∣ ∇ f ( x ) − ∇ f ( y ) ∣ ∣ ∣ ∣ x − y ∣ ∣ = ∇ 2 f ( ξ ) ≼ L ⋅ I \exist \xi \in (x,y) \Rightarrow \frac{||\nabla f(x) - \nabla f(y)||}{||x - y||} = \nabla^2 f(\xi) \preccurlyeq \mathcal L \cdot \mathcal I ∃ξ∈(x,y)⇒∣∣x−y∣∣∣∣∇f(x)−∇f(y)∣∣=∇2f(ξ)≼L⋅I
最终整理,有:
L ⋅ I − ∇ 2 f ( ξ ) ≽ 0 \mathcal L \cdot \mathcal I - \nabla^2 f(\xi) \succcurlyeq 0 L⋅I−∇2f(ξ)≽0
而不等式左侧正是 L 2 ξ T ξ − f ( ξ ) \begin{aligned}\frac{\mathcal L}{2}\xi^T\xi - f(\xi)\end{aligned} 2LξTξ−f(ξ)的二阶梯度结果。这意味着: G ( x ) = L 2 x T x − f ( x ) \begin{aligned}\mathcal G(x) = \frac{\mathcal L}{2}x^Tx - f(x)\end{aligned} G(x)=2LxTx−f(x)与二阶梯度 ∇ 2 f ( x ) ( Hessian Matrix ) \nabla^2 f(x)(\text{Hessian Matrix}) ∇2f(x)(Hessian Matrix)存在关联关系。
当然,关于二次项 x T x x^Tx xTx,我们在强凸函数的定义中也发现过这种格式:
这里也使用 G ( x ) \mathcal G(x) G(x)描述了~
G ( x ) ≜ f ( x ) − m 2 x T x \mathcal G(x) \triangleq f(x) - \frac{m}{2}x^Tx G(x)≜f(x)−2mxTx
假设这里的 G ( x ) \mathcal G(x) G(x)同样也是二阶可微的情况下,那么关于 ∇ 2 G ( x ) \nabla^2 \mathcal G(x) ∇2G(x)可表示为:
∇ 2 G ( x ) = ∇ 2 f ( x ) − m ⋅ I \nabla^2 \mathcal G(x) = \nabla^2 f(x) - m \cdot \mathcal I ∇2G(x)=∇2f(x)−m⋅I
根据强凸函数的二阶条件,必然有:
∇ 2 f ( x ) − m ⋅ I ≽ 0 \nabla^2 f(x) - m \cdot \mathcal I \succcurlyeq 0 ∇2f(x)−m⋅I≽0
梯度下降法在强凸函数上的收敛性
收敛性定理介绍
类似地,关于梯度下降法在 m m m-强凸函数上的收敛性描述表示如下:
- 条件:
- 函数 f ( ⋅ ) f(\cdot) f(⋅)向下有界,在其定义域内可微,并且 f ( ⋅ ) f(\cdot) f(⋅)是 m m m-强凸函数;
- 关于梯度函数 ∇ f ( ⋅ ) \nabla f(\cdot) ∇f(⋅)满足 L \mathcal L L-利普希兹连续;
- 在梯度下降法的迭代过程中,步长 α k ( k = 1 , 2 , 3 , ⋯ ) \alpha_k(k=1,2,3,\cdots) αk(k=1,2,3,⋯)存在明确的约束范围 α k ∈ ( 0 , 2 L + m ) \begin{aligned}\alpha_k \in \left(0,\frac{2}{\mathcal L + m}\right)\end{aligned} αk∈(0,L+m2);
- 结论:
数值解序列 { x k } k = 0 ∞ \{x_k\}_{k=0}^{\infty} {xk}k=0∞以 Q \mathcal Q Q-线性收敛的收敛速度收敛于最优数值解 x ∗ x^* x∗。关于Q \mathcal Q Q-线性收敛的数学符号描述为:∣ ∣ x k + 1 − x ∗ ∣ ∣ ∣ ∣ x k − x ∗ ∣ ∣ ≤ a ∈ ( 0 , 1 ) \begin{aligned}\frac{||x_{k+1} - x^*||}{||x_k - x^*||} \leq a \in (0,1)\end{aligned} ∣∣xk−x∗∣∣∣∣xk+1−x∗∣∣≤a∈(0,1);其他类型的收敛详见收敛速度的简单认识。该结论与凸函数的对应结论形式相同,唯一差别在于收敛速度的类型。无论使用{ x k } k = 0 ∞ \{x_k\}_{k=0}^{\infty} {xk}k=0∞还是使用{ f ( x k ) } k = 0 ∞ \{f(x_k)\}_{k=0}^{\infty} {f(xk)}k=0∞来描述收敛性,本质上是一样的。
结论分析
观察分子: ∣ ∣ x k + 1 − x ∗ ∣ ∣ ||x_{k+1} - x^*|| ∣∣xk+1−x∗∣∣,使用线搜索方法的通式对其进行表达:
分母可看作是常量,因为x k x_{k} xk是上一次迭代产生的已知信息;而最优解x ∗ x^* x∗随着函数f ( ⋅ ) f(\cdot) f(⋅)客观存在的一个值,它不会发生变化。由于是梯度下降法,因而方向P k = − ∇ f ( x k ) \mathcal P_k = -\nabla f(x_k) Pk=−∇f(xk);而当前迭代步骤下,α k \alpha_k αk是我们要求解的量,因而将其记作变量α \alpha α。
∣ ∣ x k + 1 − x ∗ ∣ ∣ = ∣ ∣ x k − α ⋅ ∇ f ( x k ) − x ∗ ∣ ∣ ||x_{k+1} - x^*|| = ||x_k -\alpha \cdot \nabla f(x_k) - x^*|| ∣∣xk+1−x∗∣∣=∣∣xk−α⋅∇f(xk)−x∗∣∣
为了证明过程中对该量进行放缩,在上述等式两侧分别执行平方操作,从而得到一个新的等式:
∣ ∣ x k + 1 − x ∗ ∣ ∣ 2 = ∣ ∣ x k − α ⋅ ∇ f ( x k ) − x ∗ ∣ ∣ 2 ||x_{k+1} - x^*||^2 = ||x_k -\alpha \cdot \nabla f(x_k) - x^*||^2 ∣∣xk+1−x∗∣∣2=∣∣xk−α⋅∇f(xk)−x∗∣∣2
对等式右侧进行展开:
-
将项x k − α ⋅ ∇ f ( x k ) − x ∗ x_k -\alpha \cdot \nabla f(x_k) - x^* xk−α⋅∇f(xk)−x∗视作项x k − x ∗ x_k - x^* xk−x∗与项α ⋅ ∇ f ( x k ) \alpha \cdot \nabla f(x_k) α⋅∇f(xk)之间的减法。 -
这里啰嗦一下:关于∣ ∣ ( x − x ∗ ) − α ⋅ ∇ f ( x k ) ∣ ∣ 2 ||(x - x^*) - \alpha \cdot \nabla f(x_k)||^2 ∣∣(x−x∗)−α⋅∇f(xk)∣∣2,可以描述成内积形式:
∣ ∣ ( x − x ∗ ) − α ⋅ ∇ f ( x k ) ∣ ∣ 2 = [ ( x − x ∗ ) − α ⋅ ∇ f ( x k ) ] T [ ( x − x ∗ ) − α ⋅ ∇ f ( x k ) ] ||(x - x^*) - \alpha \cdot \nabla f(x_k)||^2 = \left[(x - x^*) - \alpha \cdot \nabla f(x_k)\right]^T[(x - x^*) - \alpha \cdot \nabla f(x_k)] ∣∣(x−x∗)−α⋅∇f(xk)∣∣2=[(x−x∗)−α⋅∇f(xk)]T[(x−x∗)−α⋅∇f(xk)]
其中[ ( x − x ∗ ) − α ⋅ ∇ f ( x k ) ] T = [ ( x − x ∗ ) T − ( α ⋅ ∇ f ( x k ) ) T ] \left[(x - x^*) - \alpha \cdot \nabla f(x_k)\right]^T = [(x - x^*)^T - (\alpha \cdot \nabla f(x_k))^T] [(x−x∗)−α⋅∇f(xk)]T=[(x−x∗)T−(α⋅∇f(xk))T],将其替换后可得到如下三项结果:- ( x k − x ∗ ) T ( x k − x ∗ ) = ∣ ∣ x k − x ∗ ∣ ∣ 2 (x_k - x^*)^T(x_k - x^*) = ||x_k - x^*||^2 (xk−x∗)T(xk−x∗)=∣∣xk−x∗∣∣2;
- [ α ⋅ ∇ f ( x k ) ] T [ α ⋅ ∇ f ( x k ) ] = α 2 ⋅ ∣ ∣ ∇ f ( x k ) ∣ ∣ 2 [\alpha \cdot \nabla f(x_k)]^T[\alpha \cdot \nabla f(x_k)] = \alpha^2 \cdot ||\nabla f(x_k)||^2 [α⋅∇f(xk)]T[α⋅∇f(xk)]=α2⋅∣∣∇f(xk)∣∣2
其中− ( x k − x ∗ ) T [ α ⋅ ∇ f ( x k ) ] -(x_k - x^*)^T[\alpha \cdot \nabla f(x_k)] −(xk−x∗)T[α⋅∇f(xk)]与− ( x k − x ∗ ) [ α ∇ f ( x k ) ] T -(x_k - x^*)[\alpha \nabla f(x_k)]^T −(xk−x∗)[α∇f(xk)]T结果都是1 × 1 1 \times 1 1×1的标量,因而这两项相等,并将其合并在一起:
− 2 α ⋅ [ ∇ f ( x k ) ] T ( x k − x ∗ ) -2\alpha \cdot [\nabla f(x_k)]^T(x_k - x^*) −2α⋅[∇f(xk)]T(xk−x∗)
对于− 2 α ⋅ [ ∇ f ( x k ) ] T ( x k − x ∗ ) -2\alpha \cdot [\nabla f(x_k)]^T(x_k - x^*) −2α⋅[∇f(xk)]T(xk−x∗),可以继续进行描述:由于 x ∗ x^* x∗是最优数值解,那么必然有: ∇ f ( x ∗ ) = 0 \nabla f(x^*) = 0 ∇f(x∗)=0,将该式代入到上式中有:
− 2 α ⋅ [ ∇ f ( x k ) ] T ( x k − x ∗ ) = − 2 α ⋅ [ ∇ f ( x k ) − ∇ f ( x ∗ ) ] T ( x k − x ∗ ) -2\alpha \cdot [\nabla f(x_k)]^T(x_k - x^*) = -2\alpha \cdot [\nabla f(x_k) - \nabla f(x^*)]^T(x_k - x^*) −2α⋅[∇f(xk)]T(xk−x∗)=−2α⋅[∇f(xk)−∇f(x∗)]T(xk−x∗)
最终有:
∣ ∣ x k − α ⋅ ∇ f ( x k ) − x ∗ ∣ ∣ 2 = ∣ ∣ ( x − x ∗ ) − α ⋅ ∇ f ( x k ) ∣ ∣ 2 = ∣ ∣ x k − x ∗ ∣ ∣ 2 − 2 α ⋅ [ ∇ f ( x k ) − ∇ f ( x ∗ ) ] T ( x k − x ∗ ) + α 2 ∣ ∣ ∇ f ( x k ) ∣ ∣ 2 \begin{aligned} ||x_k -\alpha \cdot \nabla f(x_k) - x^*||^2 & = ||(x - x^*) - \alpha \cdot \nabla f(x_k)||^2 \\ & = ||x_k - x^*||^2 - 2 \alpha \cdot [\nabla f(x_k) - \nabla f(x^*)]^T(x_k - x^*) +\alpha^2 ||\nabla f(x_k)||^2 \end{aligned} ∣∣xk−α⋅∇f(xk)−x∗∣∣2=∣∣(x−x∗)−α⋅∇f(xk)∣∣2=∣∣xk−x∗∣∣2−2α⋅[∇f(xk)−∇f(x∗)]T(xk−x∗)+α2∣∣∇f(xk)∣∣2
从而将关注点放在寻找 [ ∇ f ( x k ) − ∇ f ( x ∗ ) ] T ( x k − x ∗ ) [\nabla f(x_k) - \nabla f(x^*)]^T(x_k - x^*) [∇f(xk)−∇f(x∗)]T(xk−x∗)的下界信息,从而关注 ∣ ∣ x k + 1 − x ∗ ∣ ∣ ∣ ∣ x k − x ∗ ∣ ∣ \begin{aligned}\frac{||x_{k+1} - x^*||}{||x_k - x^*||}\end{aligned} ∣∣xk−x∗∣∣∣∣xk+1−x∗∣∣的相关信息。
证明过程
思考:
由于函数 f ( ⋅ ) f(\cdot) f(⋅)是 m m m-强凸函数,本质上就是约束性更苛刻的凸函数,并且 ∇ f ( ⋅ ) \nabla f(\cdot) ∇f(⋅)满足 L \mathcal L L-利普希兹连续,那么根据优化算法——白老爹定理中介绍的,该函数 f ( ⋅ ) f(\cdot) f(⋅)一定满足余强制性:
∀ x 1 , x 2 ∈ R n ⇒ [ ∇ f ( x 1 ) − ∇ f ( x 2 ) ] T ( x 1 − x 2 ) ≥ 1 L ∣ ∣ ∇ f ( x 1 ) − ∇ f ( x 2 ) ∣ ∣ 2 \forall x_1,x_2 \in \mathbb R^n \Rightarrow [\nabla f(x_1) - \nabla f(x_2)]^T(x_1 - x_2) \geq \frac{1}{\mathcal L}||\nabla f(x_1) - \nabla f(x_2)||^2 ∀x1,x2∈Rn⇒[∇f(x1)−∇f(x2)]T(x1−x2)≥L1∣∣∇f(x1)−∇f(x2)∣∣2
相反地,由于 f ( ⋅ ) f(\cdot) f(⋅)是 m m m-强凸函数,因而对 [ ∇ f ( x 1 ) − ∇ f ( x 2 ) ] T ( x 1 − x 2 ) [\nabla f(x_1) - \nabla f(x_2)]^T(x_1 - x_2) [∇f(x1)−∇f(x2)]T(x1−x2)的下界描述: 1 L ∣ ∣ ∇ f ( x 1 ) − ∇ f ( x 2 ) ∣ ∣ 2 \begin{aligned}\frac{1}{\mathcal L}||\nabla f(x_1) - \nabla f(x_2)||^2\end{aligned} L1∣∣∇f(x1)−∇f(x2)∣∣2过于宽松,至少没有看到参数 m m m在余强制性中的作用。因而我们需要找到一个更严格的下界。
回归证明过程:
由于 f ( ⋅ ) f(\cdot) f(⋅)是 m m m-强凸函数,根据强凸函数的定义,令 G ( x ) ≜ f ( x ) − m 2 x T x \begin{aligned}\mathcal G(x) \triangleq f(x) - \frac{m}{2} x^Tx\end{aligned} G(x)≜f(x)−2mxTx,必然有: G ( x ) \mathcal G(x) G(x)是凸函数。
充分必要条件~
由于 f ( ⋅ ) f(\cdot) f(⋅)可微,并且 m 2 x T x \begin{aligned}\frac{m}{2}x^Tx\end{aligned} 2mxTx是关于 x x x的二次函数——必然在定义域内可微。因此:函数 G ( ⋅ ) \mathcal G(\cdot) G(⋅)在定义域内可微。对应梯度 ∇ G ( x ) \nabla \mathcal G(x) ∇G(x)表示为:
∇ G ( x ) = ∇ [ f ( x ) − m 2 x T x ] = ∇ f ( x ) − m ⋅ x \nabla \mathcal G(x) = \nabla \left[f(x) - \frac{m}{2}x^Tx\right] = \nabla f(x) - m \cdot x ∇G(x)=∇[f(x)−2mxTx]=∇f(x)−m⋅x
思考:
又因为 ∇ f ( ⋅ ) \nabla f(\cdot) ∇f(⋅)满足 L \mathcal L L-利普希兹连续,那么 G ( ⋅ ) \mathcal G(\cdot) G(⋅)是否也满足利普希兹连续 ? ? ? 必然是满足的。可以从定义角度观察 ⇒ \Rightarrow ⇒ ∣ ∣ ∇ G ( x ) − ∇ G ( y ) ∣ ∣ ||\nabla \mathcal G(x) - \nabla \mathcal G(y)|| ∣∣∇G(x)−∇G(y)∣∣与 ∣ ∣ x − y ∣ ∣ ||x - y|| ∣∣x−y∣∣之间的关联关系:
将∇ G ( x ) = ∇ f ( x ) − m ⋅ x \nabla \mathcal G(x) =\nabla f(x) - m \cdot x ∇G(x)=∇f(x)−m⋅x代入~使用三角不等式:∣ ∣ [ ∇ f ( x ) − ∇ f ( y ) ] − m ( x − y ) ∣ ∣ ≤ ∣ ∣ ∇ f ( x ) − ∇ f ( y ) ∣ ∣ + ∣ ∣ m ⋅ ( x − y ) ∣ ∣ ||[\nabla f(x) - \nabla f(y)] - m(x - y)|| \leq ||\nabla f(x) - \nabla f(y)|| + ||m \cdot (x - y)|| ∣∣[∇f(x)−∇f(y)]−m(x−y)∣∣≤∣∣∇f(x)−∇f(y)∣∣+∣∣m⋅(x−y)∣∣利用利普希兹连续将∣ ∣ ∇ f ( x ) − ∇ f ( y ) ∣ ∣ ||\nabla f(x) - \nabla f(y)|| ∣∣∇f(x)−∇f(y)∣∣替换成L ⋅ ∣ ∣ x − y ∣ ∣ \mathcal L \cdot ||x - y|| L⋅∣∣x−y∣∣,不等号不发生变化。
∣ ∣ ∇ G ( x ) − ∇ G ( y ) ∣ ∣ = ∣ ∣ ∇ f ( x ) − ∇ f ( y ) − m ( x − y ) ∣ ∣ ≤ ∣ ∣ ∇ f ( x ) − ∇ f ( y ) ∣ ∣ + ∣ ∣ m ⋅ ( x − y ) ∣ ∣ ≤ L ⋅ ∣ ∣ x − y ∣ ∣ + m ⋅ ∣ ∣ x − y ∣ ∣ = ( L + m ) ⋅ ∣ ∣ x − y ∣ ∣ \begin{aligned} ||\nabla \mathcal G(x) - \nabla \mathcal G(y)|| & = ||\nabla f(x) - \nabla f(y) - m (x - y)|| \\ & \leq ||\nabla f(x) - \nabla f(y)|| + ||m \cdot (x - y)|| \\ & \leq \mathcal L \cdot ||x - y|| + m \cdot ||x - y|| \\ & = (\mathcal L + m) \cdot||x - y|| \end{aligned} ∣∣∇G(x)−∇G(y)∣∣=∣∣∇f(x)−∇f(y)−m(x−y)∣∣≤∣∣∇f(x)−∇f(y)∣∣+∣∣m⋅(x−y)∣∣≤L⋅∣∣x−y∣∣+m⋅∣∣x−y∣∣=(L+m)⋅∣∣x−y∣∣
虽然通过一个简单的证明确定了 ∇ G ( ⋅ ) \nabla \mathcal G(\cdot) ∇G(⋅)满足利普希兹连续,并得到了一个关于 ∇ G ( ⋅ ) \nabla \mathcal G(\cdot) ∇G(⋅)的利普希兹常数: L + m \mathcal L + m L+m,但这个常数并不合理。因为相比于 ∇ f ( ⋅ ) \nabla f(\cdot) ∇f(⋅), ∇ G ( ⋅ ) \nabla \mathcal G(\cdot) ∇G(⋅)的约束强度变低了:
关于函数 G ( ⋅ ) \mathcal G(\cdot) G(⋅)的斜率变化范围反而大于 f ( ⋅ ) f(\cdot) f(⋅)。
∃ ξ ∈ ( x , y ) ⇒ ∣ ∣ ∇ G ( x ) − ∇ G ( y ) ∣ ∣ ∣ ∣ x − y ∣ ∣ = G ′ ( ξ ) ≤ L + m \exist \xi \in (x,y) \Rightarrow\frac{||\nabla \mathcal G(x) - \nabla \mathcal G(y)||}{||x - y||} = \mathcal G'(\xi) \leq \mathcal L + m ∃ξ∈(x,y)⇒∣∣x−y∣∣∣∣∇G(x)−∇G(y)∣∣=G′(ξ)≤L+m
我们希望能够找到一个约束性更强的利普希兹常数,而不是 L + m \mathcal L + m L+m。
回归证明过程:
如果令 H ( x ) ≜ L 2 x T x − f ( x ) \begin{aligned}\mathcal H(x) \triangleq \frac{\mathcal L}{2} x^Tx - f(x)\end{aligned} H(x)≜2LxTx−f(x),根据白老爹定理, H ( x ) \mathcal H(x) H(x)必然也是凸函数。将 f ( x ) f(x) f(x)使用 G ( x ) \mathcal G(x) G(x)进行替换:
{ f ( x ) = G ( x ) + m 2 x T x H ( x ) ≜ L 2 x T x − m 2 x T x − G ( x ) = L − m 2 x T x − G ( x ) \begin{cases} \begin{aligned} f(x) & = \mathcal G(x) + \frac{m}{2} x^Tx \\ \mathcal H(x) & \triangleq \frac{\mathcal L}{2}x^Tx - \frac{m}{2}x^Tx - \mathcal G(x) \\ & = \frac{\mathcal L - m}{2} x^Tx - \mathcal G(x) \end{aligned} \end{cases} ⎩ ⎨ ⎧f(x)H(x)=G(x)+2mxTx≜2LxTx−2mxTx−G(x)=2L−mxTx−G(x)
观察这个新式子: H ( x ) = L − m 2 x T x − G ( x ) \begin{aligned}\mathcal H(x) = \frac{\mathcal L - m}{2} x^Tx - \mathcal G(x)\end{aligned} H(x)=2L−mxTx−G(x),由于 H ( x ) , G ( x ) \mathcal H(x),\mathcal G(x) H(x),G(x)都是凸函数,那么可以再次使用白老爹定理,可推出: G ( ⋅ ) \mathcal G(\cdot) G(⋅)的梯度 ∇ G ( ⋅ ) \nabla \mathcal G(\cdot) ∇G(⋅)满足余强制性。即:
其中G ( x ) \mathcal G(x) G(x)为凸函数是前提条件;H ( x ) \mathcal H(x) H(x)为凸函数是其中一个等价条件。对应描述余强制性不等式的系数由1 L \begin{aligned}\frac{1}{\mathcal L}\end{aligned} L1变为1 L − m \begin{aligned}\frac{1}{\mathcal L - m}\end{aligned} L−m1。实际上,关于白老爹定理的最后一个等价条件也是满足的。即:∇ G ( ⋅ ) \nabla \mathcal G(\cdot) ∇G(⋅)满足 ( L − m ) (\mathcal L - m) (L−m)-利普希兹连续。与之前的( L + m ) (\mathcal L + m) (L+m)-利普希兹连续相反,它的约束性比L \mathcal L L-利普希兹连续更强了。
[ ∇ G ( x ) − ∇ G ( y ) ] T ( x − y ) ≥ 1 L − m ∣ ∣ ∇ G ( x ) − ∇ G ( y ) ∣ ∣ 2 [\nabla \mathcal G(x) - \nabla \mathcal G(y)]^T(x - y) \geq \frac{1}{\mathcal L - m} ||\nabla \mathcal G(x) - \nabla \mathcal G(y)||^2 [∇G(x)−∇G(y)]T(x−y)≥L−m1∣∣∇G(x)−∇G(y)∣∣2
( 2023 / 8 / 20 ) (2023/8/20) (2023/8/20):关于为什么凸函数 G ( ⋅ ) \mathcal G(\cdot) G(⋅)相比 m − m- m−强凸函数 f ( ⋅ ) f(\cdot) f(⋅)在利普希兹连续的角度有更强的约束性,个人错误的认为是凸函数与强凸函数之间的差异性导致的。(错误想法)
因为强凸函数、凸函数之间的差异性主要体现在下界;而利普希兹连续( L ; L − m ) (\mathcal L;\mathcal L - m) (L;L−m)约束描述的是上界。
\quad
正确的逻辑思路是:关于凸函数 G ( x ) ≜ f ( x ) − m 2 x T x \begin{aligned}\mathcal G(x) \triangleq f(x) - \frac{m}{2} x^Tx \end{aligned} G(x)≜f(x)−2mxTx,我们可以将其理解为:在凸函数 f ( x ) f(x) f(x)的基础上,减掉了一部分恒正二次项系数 ( m > 0 ) (m > 0) (m>0),从而相比于 f ( x ) f(x) f(x), G ( x ) \mathcal G(x) G(x)函数凸的效果有所减小。这才是导致其利普希兹常数 ( L − m ) < f ( x ) (\mathcal L - m) < f(x) (L−m)<f(x)利普希兹常数 ( L ) (\mathcal L) (L)的真正原因。
基于该结论,将 ∇ G ( x ) = ∇ f ( x ) − m ⋅ x \nabla \mathcal G(x) = \nabla f(x) - m \cdot x ∇G(x)=∇f(x)−m⋅x代入,有:
我们的目标是凑出 [ ∇ f ( x ) − ∇ f ( y ) ] T ( x − y ) [\nabla f(x) - \nabla f(y)]^T(x - y) [∇f(x)−∇f(y)]T(x−y)。
[ ∇ f ( x ) − ∇ f ( y ) − m ⋅ ( x − y ) ] T ( x − y ) ≥ 1 L − m ∣ ∣ ∇ f ( x ) − ∇ f ( y ) − m ⋅ ( x − y ) ∣ ∣ 2 [\nabla f(x) - \nabla f(y) - m\cdot (x - y)]^T (x - y) \geq \frac{1}{\mathcal L - m} ||\nabla f(x) - \nabla f(y) - m \cdot (x - y)||^2 [∇f(x)−∇f(y)−m⋅(x−y)]T(x−y)≥L−m1∣∣∇f(x)−∇f(y)−m⋅(x−y)∣∣2
由于 [ ( ∇ f ( x ) − ∇ f ( y ) ) − m ⋅ ( x − y ) ] T = [ ∇ f ( x ) − ∇ f ( y ) ] T − m ⋅ ( x − y ) T [(\nabla f(x) - \nabla f(y)) - m \cdot (x - y)]^T = [\nabla f(x) - \nabla f(y)]^T - m\cdot (x - y)^T [(∇f(x)−∇f(y))−m⋅(x−y)]T=[∇f(x)−∇f(y)]T−m⋅(x−y)T,因此将不等式左侧继续展开:
展开过程中将m ⋅ ( x − y ) T ( x − y ) m \cdot (x - y)^T(x - y) m⋅(x−y)T(x−y)写成范数平方的形式:m ⋅ ∣ ∣ x − y ∣ ∣ 2 m \cdot ||x - y||^2 m⋅∣∣x−y∣∣2关于不等式右侧的范数平方可看作上述两项∇ f ( x ) − ∇ f ( y ) \nabla f(x) - \nabla f(y) ∇f(x)−∇f(y)与m ⋅ ( x − y ) m \cdot (x - y) m⋅(x−y)差的平方形式,使用完全平方公式进行展开。
[ ∇ f ( x ) − ∇ f ( y ) ] T ( x − y ) − m ⋅ ∣ ∣ x − y ∣ ∣ 2 ≥ 1 L − m { ∣ ∣ ∇ f ( x ) − ∇ f ( y ) ∣ ∣ 2 + m 2 ⋅ ∣ ∣ x − y ∣ ∣ 2 − 2 m ⋅ [ ∇ f ( x ) − ∇ f ( y ) ] T ( x − y ) } [\nabla f(x) - \nabla f(y)]^T(x - y) - m \cdot ||x - y||^2 \geq \frac{1}{\mathcal L - m} \left\{||\nabla f(x) - \nabla f(y)||^2 + m^2 \cdot ||x - y||^2 - 2m \cdot [\nabla f(x) - \nabla f(y)]^T(x - y)\right\} [∇f(x)−∇f(y)]T(x−y)−m⋅∣∣x−y∣∣2≥L−m1{∣∣∇f(x)−∇f(y)∣∣2+m2⋅∣∣x−y∣∣2−2m⋅[∇f(x)−∇f(y)]T(x−y)}
将不等式右侧的含 [ ∇ f ( x ) − ∇ f ( y ) ] T ( x − y ) [\nabla f(x) - \nabla f(y)]^T(x - y) [∇f(x)−∇f(y)]T(x−y)的项移到不等式左侧,同时将不等式左侧的含 ∣ ∣ x − y ∣ ∣ 2 ||x - y||^2 ∣∣x−y∣∣2的项移到不等式右侧,从而有:
此时不等式左侧仅包含关于[ ∇ f ( x ) − ∇ f ( y ) ] T ( x − y ) [\nabla f(x) - \nabla f(y)]^T(x - y) [∇f(x)−∇f(y)]T(x−y)项的信息。
( 1 + 2 m L − m ) [ ∇ f ( x ) − ∇ f ( y ) ] T ( x − y ) ≥ 1 L − m ∣ ∣ ∇ f ( x ) − ∇ f ( y ) ∣ ∣ 2 + ( m + m 2 L − m ) ∣ ∣ x − y ∣ ∣ 2 \left(1 + \frac{2m}{\mathcal L - m} \right)[\nabla f(x) - \nabla f(y)]^T (x - y) \geq \frac{1}{\mathcal L - m}||\nabla f(x) - \nabla f(y)||^2 + \left(m + \frac{m^2}{\mathcal L - m}\right)||x - y||^2 (1+L−m2m)[∇f(x)−∇f(y)]T(x−y)≥L−m1∣∣∇f(x)−∇f(y)∣∣2+(m+L−mm2)∣∣x−y∣∣2
继续化简,有
由于 L , m \mathcal L,m L,m分别是约束 ∇ 2 f ( ⋅ ) \nabla^2 f(\cdot) ∇2f(⋅)上界与下界的常数参数,由于 f ( ⋅ ) f(\cdot) f(⋅)是强凸函数,那么 L > m \mathcal L> m L>m恒成立。
如果L < m \mathcal L < m L<m,即上界小于下界,那就不是凸函数了~如果L = m \mathcal L = m L=m,例如线性函数,那么它只是凸函数,而不是强凸函数。
因而将不等式左侧的系数 L + m L − m \begin{aligned}\frac{\mathcal L + m}{\mathcal L - m}\end{aligned} L−mL+m移到右侧,不等号方向不变。此时,不等式左侧只剩下了 [ ∇ f ( x ) − ∇ f ( y ) ] T ( x − y ) [\nabla f(x) - \nabla f(y)]^T(x - y) [∇f(x)−∇f(y)]T(x−y)。
L + m L − m [ ∇ f ( x ) − ∇ f ( y ) ] T ( x − y ) ≥ 1 L − m ∣ ∣ ∇ f ( x ) − ∇ f ( y ) ∣ ∣ 2 + L ⋅ m L − m ∣ ∣ x − y ∣ ∣ 2 ⇒ [ ∇ f ( x ) − ∇ f ( y ) ] T ( x − y ) ≥ ( 1 L − m ⋅ L − m L + m ) ∣ ∣ ∇ f ( x ) − ∇ f ( y ) ∣ ∣ 2 + ( L ⋅ m L − m ⋅ L − m L + m ) ∣ ∣ x − y ∣ ∣ 2 = [ ∇ f ( x ) − ∇ f ( y ) ] T ( x − y ) ≥ 1 L + m ∣ ∣ ∇ f ( x ) − ∇ f ( y ) ∣ ∣ 2 + L ⋅ m L + m ∣ ∣ x − y ∣ ∣ 2 \begin{aligned} & \quad \frac{\mathcal L + m}{\mathcal L - m}[\nabla f(x) - \nabla f(y)]^T (x - y) \geq \frac{1}{\mathcal L - m}||\nabla f(x) - \nabla f(y)||^2 + \frac{\mathcal L \cdot m}{\mathcal L - m}||x - y||^2 \\ & \quad \\ & \Rightarrow [\nabla f(x) - \nabla f(y)]^T(x - y) \geq \left(\frac{1}{\mathcal L - m} \cdot \frac{\mathcal L - m}{\mathcal L + m}\right) ||\nabla f(x) - \nabla f(y)||^2 + \left(\frac{\mathcal L \cdot m}{\mathcal L - m} \cdot \frac{\mathcal L - m}{\mathcal L + m}\right) ||x-y||^2 \\ & = [\nabla f(x) - \nabla f(y)]^T(x - y) \geq \frac{1}{\mathcal L + m} ||\nabla f(x) - \nabla f(y)||^2 + \frac{\mathcal L \cdot m}{\mathcal L + m} ||x-y||^2 \end{aligned} L−mL+m[∇f(x)−∇f(y)]T(x−y)≥L−m1∣∣∇f(x)−∇f(y)∣∣2+L−mL⋅m∣∣x−y∣∣2⇒[∇f(x)−∇f(y)]T(x−y)≥(L−m1⋅L+mL−m)∣∣∇f(x)−∇f(y)∣∣2+(L−mL⋅m⋅L+mL−m)∣∣x−y∣∣2=[∇f(x)−∇f(y)]T(x−y)≥L+m1∣∣∇f(x)−∇f(y)∣∣2+L+mL⋅m∣∣x−y∣∣2
至此,回顾结论分析,由于 x , y ∈ R n x,y \in \mathbb R^n x,y∈Rn内任意取值,因此令: x = x k ; y = x ∗ x = x_k;y = x^* x=xk;y=x∗,上式有:
关于不等式右侧的 ∇ f ( x ∗ ) = 0 \nabla f(x^*) =0 ∇f(x∗)=0这里就省略了~
[ ∇ f ( x k ) − ∇ f ( x ∗ ) ] T ( x k − x ∗ ) ≥ 1 L + m ∣ ∣ ∇ f ( x k ) ∣ ∣ 2 + L ⋅ m L + m ∣ ∣ x k − x ∗ ∣ ∣ 2 [\nabla f(x_k) - \nabla f(x^*)]^T(x_k - x^*) \geq \frac{1}{\mathcal L + m} ||\nabla f(x_k)||^2 + \frac{\mathcal L \cdot m}{\mathcal L + m}||x_k - x^*||^2 [∇f(xk)−∇f(x∗)]T(xk−x∗)≥L+m1∣∣∇f(xk)∣∣2+L+mL⋅m∣∣xk−x∗∣∣2
从而将这个描述 [ ∇ f ( x k ) − ∇ f ( x ∗ ) ] T ( x k − x ∗ ) [\nabla f(x_k) - \nabla f(x^*)]^T(x_k - x^*) [∇f(xk)−∇f(x∗)]T(xk−x∗)下界的不等式代回到结论分析的式子中有:
由于− 2 α -2\alpha −2α使不等号方向发生变化~合并同类项~
∣ ∣ x k − α ⋅ ∇ f ( x k ) − x ∗ ∣ ∣ 2 = ∣ ∣ x k − x ∗ ∣ ∣ 2 − 2 α ⋅ [ ∇ f ( x k ) − ∇ f ( x ∗ ) ] T ( x k − x ∗ ) + α 2 ∣ ∣ ∇ f ( x k ) ∣ ∣ 2 ≤ ∣ ∣ x k − x ∗ ∣ ∣ 2 − 2 α ( 1 L + m ∣ ∣ ∇ f ( x k ) ∣ ∣ 2 + L ⋅ m L + m ∣ ∣ x k − x ∗ ∣ ∣ 2 ) + α 2 ∣ ∣ ∇ f ( x k ) ∣ ∣ 2 ≤ ∣ ∣ x k − x ∗ ∣ ∣ 2 − 2 α L + m ∣ ∣ ∇ f ( x k ) ∣ ∣ 2 − 2 α L m L + m ∣ ∣ x k − x ∗ ∣ ∣ 2 + α 2 ∣ ∣ ∇ f ( x k ) ∣ ∣ 2 = ( 1 − 2 α L m L + m ) ∣ ∣ x k − x ∗ ∣ ∣ 2 + α ( α − 2 L + m ) ∣ ∣ ∇ f ( x k ) ∣ ∣ 2 \begin{aligned} ||x_k -\alpha \cdot \nabla f(x_k) - x^*||^2 & = ||x_k - x^*||^2 - 2 \alpha \cdot [\nabla f(x_k) - \nabla f(x^*)]^T(x_k - x^*) +\alpha^2 ||\nabla f(x_k)||^2 \\ & \leq ||x_k- x^*||^2 - 2\alpha \left(\frac{1}{\mathcal L + m} ||\nabla f(x_k)||^2 + \frac{\mathcal L \cdot m}{\mathcal L + m}||x_k - x^*||^2\right) + \alpha^2 ||\nabla f(x_k)||^2 \\ & \leq ||x_k- x^*||^2 - \frac{2 \alpha}{\mathcal L + m} ||\nabla f(x_k)||^2 - \frac{2\alpha \mathcal L m}{\mathcal L + m}||x_k - x^*||^2 + \alpha^2 ||\nabla f(x_k)||^2 \\ & = \left(1 - \frac{2 \alpha \mathcal L m}{\mathcal L + m}\right) ||x_k - x^*||^2 + \alpha \left(\alpha - \frac{2}{\mathcal L + m}\right) ||\nabla f(x_k)||^2 \end{aligned} ∣∣xk−α⋅∇f(xk)−x∗∣∣2=∣∣xk−x∗∣∣2−2α⋅[∇f(xk)−∇f(x∗)]T(xk−x∗)+α2∣∣∇f(xk)∣∣2≤∣∣xk−x∗∣∣2−2α(L+m1∣∣∇f(xk)∣∣2+L+mL⋅m∣∣xk−x∗∣∣2)+α2∣∣∇f(xk)∣∣2≤∣∣xk−x∗∣∣2−L+m2α∣∣∇f(xk)∣∣2−L+m2αLm∣∣xk−x∗∣∣2+α2∣∣∇f(xk)∣∣2=(1−L+m2αLm)∣∣xk−x∗∣∣2+α(α−L+m2)∣∣∇f(xk)∣∣2
根据收敛性定理中关于步长 α \alpha α的条件: α ∈ ( 0 , 2 L + m ) \begin{aligned}\alpha \in \left(0, \frac{2}{\mathcal L + m}\right) \end{aligned} α∈(0,L+m2),有:
很明显,项 α ( α − 2 L + m ) ∣ ∣ ∇ f ( x k ) ∣ ∣ 2 \begin{aligned}\alpha \left(\alpha - \frac{2}{\mathcal L + m}\right) ||\nabla f(x_k)||^2\end{aligned} α(α−L+m2)∣∣∇f(xk)∣∣2是一个负值,从而可以对 ∣ ∣ x k = α ⋅ ∇ f ( x k ) − x ∗ ∣ ∣ 2 ||x_k = \alpha \cdot \nabla f(x_k) - x^*||^2 ∣∣xk=α⋅∇f(xk)−x∗∣∣2进行进一步的约束。
∣ ∣ x k − α ⋅ ∇ f ( x k ) − x ∗ ∣ ∣ 2 ≤ ( 1 − α ⋅ 2 L m L + m ) ∣ ∣ x k − x ∗ ∣ ∣ 2 \begin{aligned} ||x_k -\alpha \cdot \nabla f(x_k) - x^*||^2 \leq \left(1 - \alpha \cdot \frac{2 \mathcal L m}{\mathcal L + m}\right) ||x_k - x^*||^2 \end{aligned} ∣∣xk−α⋅∇f(xk)−x∗∣∣2≤(1−α⋅L+m2Lm)∣∣xk−x∗∣∣2
最终移项并开根号,得到关于收敛速度定义的一个表达:
关于收敛速度,详见收敛速度的简单认识。
∣ ∣ x k − α ⋅ ∇ f ( x k ) − x ∗ ∣ ∣ ∣ ∣ x k − x ∗ ∣ ∣ ≤ 1 − α ⋅ 2 L m L + m \begin{aligned}\frac{||x_k - \alpha \cdot \nabla f(x_k) -x^*||}{||x_k - x^*||} \leq \sqrt{1 - \alpha \cdot \frac{2\mathcal L m}{\mathcal L + m}} \end{aligned} ∣∣xk−x∗∣∣∣∣xk−α⋅∇f(xk)−x∗∣∣≤1−α⋅L+m2Lm
记 C = 1 − α ⋅ 2 L m L + m \begin{aligned}\mathcal C = 1 - \alpha \cdot \frac{2\mathcal L m}{\mathcal L + m}\end{aligned} C=1−α⋅L+m2Lm,观察:
- 由于: α , L , m \alpha,\mathcal L,m α,L,m均 > 0 >0 >0,因而 C < 1 \mathcal C <1 C<1;
- 根据 α \alpha α条件: α < 2 L + m \begin{aligned}\alpha < \frac{2}{\mathcal L + m}\end{aligned} α<L+m2,因而将该式代入,有:
C = 1 − α ⋅ 2 L m L + m > 1 − 4 L m ( L + m ) 2 = ( L + m ) 2 − 4 L m ( L + m ) 2 = ( L − m ) 2 ( L + m ) 2 \begin{aligned}\mathcal C = 1 - \alpha \cdot \frac{2\mathcal L m}{\mathcal L + m} > 1 -\frac{4 \mathcal L m}{(\mathcal L + m)^2} = \frac{(\mathcal L + m)^2 - 4\mathcal L m}{(\mathcal L + m)^2} = \frac{(\mathcal L - m)^2}{(\mathcal L + m)^2}\end{aligned} C=1−α⋅L+m2Lm>1−(L+m)24Lm=(L+m)2(L+m)2−4Lm=(L+m)2(L−m)2
由于 L , m \mathcal L,m L,m恒正,必然有: ( L − m ) 2 ( L + m ) 2 > 0 \begin{aligned}\frac{(\mathcal L - m)^2}{(\mathcal L + m)^2} > 0\end{aligned} (L+m)2(L−m)2>0
从而最终有: C ∈ ( 0 , 1 ) \mathcal C \in (0,1) C∈(0,1),从而 C ∈ ( 0 , 1 ) \sqrt \mathcal C \in (0,1) C∈(0,1)。即:
∣ ∣ x k + 1 − x ∗ ∣ ∣ ∣ ∣ x k − x ∗ ∣ ∣ = ∣ ∣ x k − α ⋅ ∇ f ( x k ) − x ∗ ∣ ∣ ∣ ∣ x k − x ∗ ∣ ∣ ≤ C ∈ ( 0 , 1 ) \begin{aligned}\frac{||x_{k+1} -x^*||}{||x_k - x^*||} = \frac{||x_k - \alpha \cdot \nabla f(x_k) -x^*||}{||x_k - x^*||} \leq \sqrt{\mathcal C} \in (0,1) \end{aligned} ∣∣xk−x∗∣∣∣∣xk+1−x∗∣∣=∣∣xk−x∗∣∣∣∣xk−α⋅∇f(xk)−x∗∣∣≤C∈(0,1)
因而 { x k } k = 0 ∞ \{x_k\}_{k=0}^{\infty} {xk}k=0∞的收敛速度是 Q \mathcal Q Q-线性收敛,证毕。
相关参考:
【优化算法】梯度下降法-强凸函数的收敛性分析(上)