15.树与二叉树基础

一. 树，基本术语

二. 二叉树

（1）二叉树

（2）满二叉树

（3）完全二叉树

三. 二叉树的性质

四. 二叉树的存储结构

（1）顺序存储结构

（2）链式存储结构

树形结构：结点之间有分支，具有层次关系。

一. 树，基本术语

树的定义：树(Tree)是n (n≥0)个结点的有限集。
（1）若n = 0，称为空树；
（2）若n >0，则它满足如下两个条件：

有且仅有一个特定的称为根(Root)的结点；
其余结点可分为m(m≥0)个互不相交的有限集T1,T2,T3,....Tm，其中每一个集合本身又是一棵树，并称为根的子树(SubTree)。

树的一些基本术语在下图中展示：

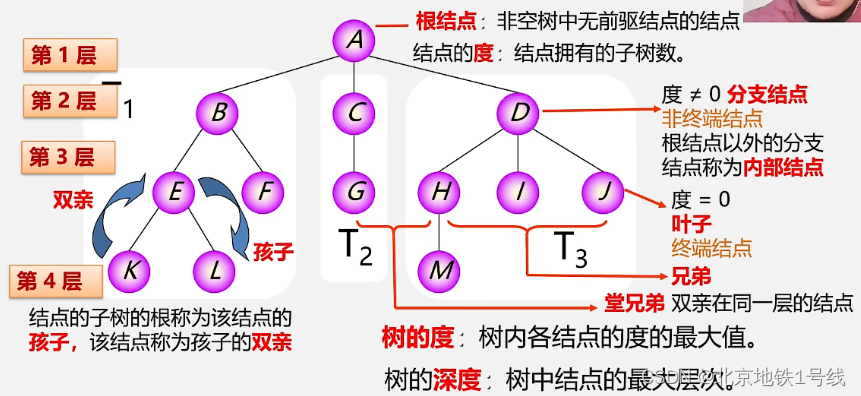
有序树：树中结点的各子树从左至右有次序(最左边的为第一个孩子)。

无序树：树中结点的各子树无次序。

森林：是m(m≥O)棵互不相交的树的集合。

森林与树的关系：把树的根结点删除树就变成了森林。一棵树可以看成是一个特殊的森林。给森林中的各子树加上一个双亲结点，森林就变成了树。

二. 二叉树

（1）二叉树

为何要重点研究每结点最多只有两个“叉”的树？

二叉树的结构最简单，规律性最强;
可以证明，所有树都能转为唯一对应的二叉树，不失一般性。

普通树(多叉树)若不转化为二叉树，则运算很难实现。二叉树在树结构的应用中起着非常重要的作用，因为对二叉的许多操作算法简单，而任何树都可以与二叉树相互转换，这样就解决了。

二叉树：二叉树是n(n≥0)个结点的有限集，它或者是空集(n = 0)，或者由一个根结点及两棵互不相交的，分别称作这个根的左子树和右子树的二叉树组成。
二叉树的特点：

每个结点最多有俩孩子(二叉树中不存在度大于2的结点)。
子树有左右之分，其次序不能颠倒。
二叉树可以是空集合，根订以有空的左子树或空的右子树。

注意：二叉树不是树的特殊情况，也不是有序树，而是两个不同的概念。

二叉树结点的子树要区分左子树和右子树，即使只有一棵子树也行区分，说明它是左子树，还是右子树。
树当结点只有一个孩子时，就无须区分它是左还是右的次序。因此二者是不同的。这是二叉树与树的最主要的差别。

也就是二叉树每个结点位置或者说次序都是固定的，可以是空，但是不可以说它没有位置，而树的结点位置是相对于别的结点来说的，没有别的结点时，它就无所谓左右了。

二叉树的五种基本形态如下：

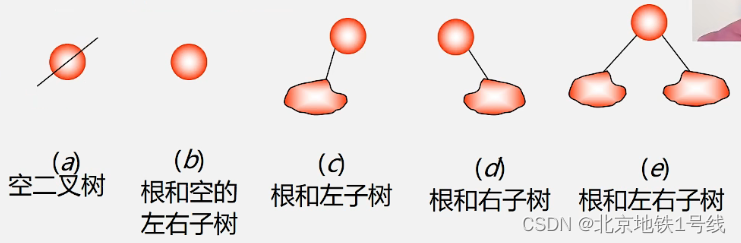
下面我们介绍满二叉树和完全二叉树，这两种特殊的二叉树在顺序存储结构下可以复原。

（2）满二叉树

一棵深度为k且有 $2^k-1$ 个结点的二叉树称为满二叉树。

特点：1.每一层上的结点数都是最大结数(即每层都满)；2.叶子节点全部在最底层； 3.满二叉树在同样深度的二叉树中，结点数，叶子结点数都是最多的。

对满二叉树结点位置进行编号：从根结点开始，自上而下，自左而右。每一结点位置都有元素。

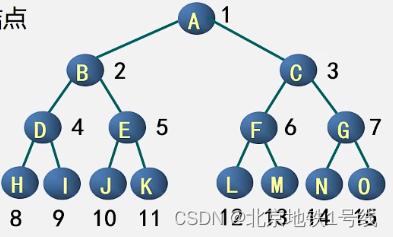
（3）完全二叉树

深度为k的具有n个结点的二叉树，当且仅当其每一个结点都与深度为k的满二叉树中编号为1~n的结点一一对应时，称之为完全二叉树。

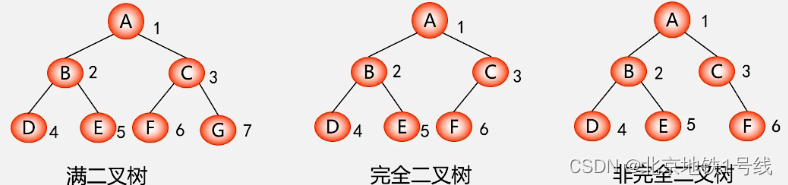
也可以从满二叉树看完全二叉树：在满二叉树中，从最后一个结点开始，连续去掉任意个结点，即是一棵完全二叉树。一定是连续的去掉!

特点：1.叶子结点只可能分布在层次最大的两层上；2.对任一结点，如果其右子树的最大层次为i,则其左子树的最大层次必为i或i+1。

三. 二叉树的性质

性质1：二叉树的第i层上最多有 $2^{i-1}$ 个结点（i>=1），最少有1个结点；

性质2：深度为k的二叉树至多有 $2^k-1$ 个结点，最少有k个结点；

性质3：对任何一个二叉树T，如果叶子结点数为n0，度为2的结点数为n2，则有： $n_0=n_2+1$ ；

证明：设总边数为B，结点数为n，显然有： $B=n-1$ ，这是由于除了根结点以外，每个结点有且只有一个前驱。

同时，因为结点的度只能为0，1，2，记他们的个数分别是 $n_0,n_1,n_2$ ，所以有： $n=n_0+n_1+n_2$ 和 $B=n_1+2n_2$ ；

联立以上三式就可得到： $n_0=n_2+1$ ，证毕。

性质4：具有n个结点的完全二叉树的深度是 $\left \lfloor log_2n \right \rfloor+1$ ，其中 $\left \lfloor x \right \rfloor$ 表示不超过x的最大整数。

证明：深度为k的完全二叉树，结点个数的范围是： $2^{k-1}\leqslant n\leqslant 2^k-1$

性质5：对一个具有n个结点的完全二叉树，对一个编号为i的结点：

（1）i>1时，此结点的双亲结点是 $\left \lfloor i/2 \right \rfloor$ ；

（2）此结点的左孩子结点编号是 $2i$ ，右孩子结点编号是 $2i+1$ （如果左右孩子存在）；

四. 二叉树的存储结构

（1）顺序存储结构

实现：按满二叉树的结点层次编号，依次存放二叉树中的数据元素。

//二叉树的顺序存储
# define MAXSIZE 100
typedef TElemType SqBiTree[MAXSIZE];
SqBiTree bt;

定义二叉树的顺序存储结构如上所示，使用了一个数组 SqBiTree 来表示二叉树。SqBiTree 是一个 typedef 定义的类型别名，它是一个大小为 MAXSIZE 的数组，数组元素的类型是 TElemType。TElemType 可以根据具体的需求来定义，表示二叉树节点的数据类型。在这段代码中没有给出 TElemType 的具体定义，需要根据实际情况来确定。通过这段代码，我们可以使用数组 bt 来表示一个二叉树，数组的大小为 MAXSIZE，数组中的元素存储了二叉树的节点数据。这种顺序存储结构的好处是可以快速访问二叉树的任意节点，但是需要提前确定二叉树的最大节点数。

例：根据数组还原二叉树

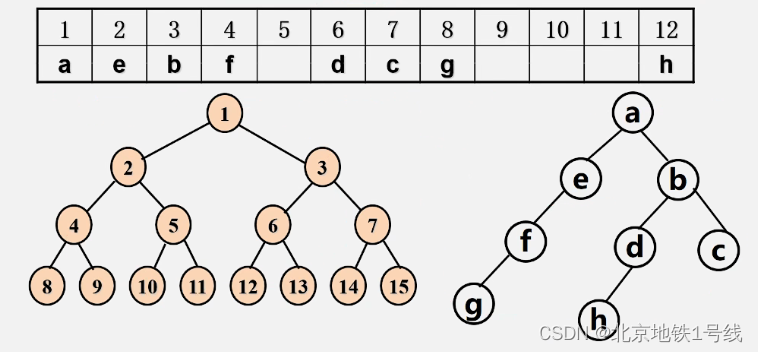
特点：结点间关系蕴含在数组位置中，浪费空间，适用于满二叉树和完全二叉树。

（2）链式存储结构

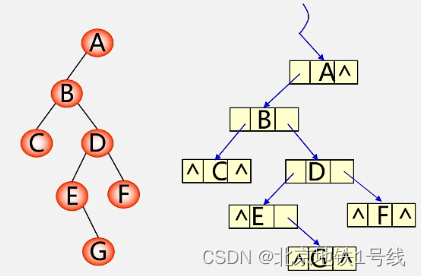
二叉树结点的特点：每个结点有左孩子，或者右孩子，所以二叉树的链式结点包含数据域和两个指针域：

typedef struct BiNode{TElemType data;struct BiNode *lchild,*rchild; //左右孩子指针
}BiNode,*BiTree;

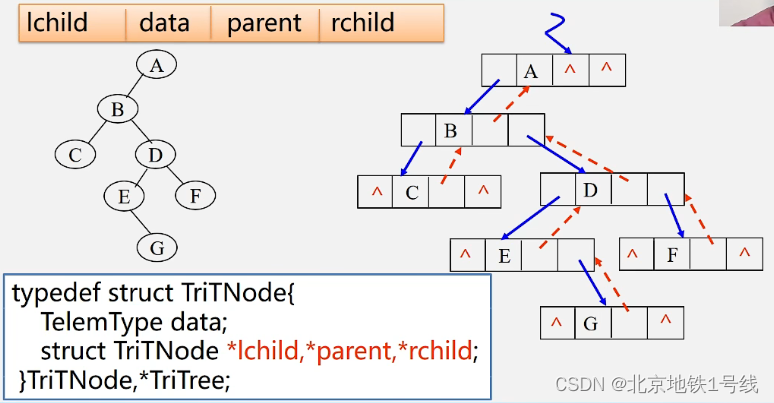
有时为了寻找祖先结点，还会增设一个指针*parent，这样结点就有四部分：

lchild

data

parent

rchild

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/104852.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！