在我们建立一个学习算法时,或者说训练一个模型时,我们总是希望最大化某一个给定的评价指标(比如说准确度Acc),但算法在学习过程中又会尝试优化某一个损失函数(比如说均方差MSE或者交叉熵Cross-entropy)。
那为什么不把评价指标matric作为学习算法的损失函数loss呢?
抛开复杂的数学,我们可以这么理解,机器学习的评估函数主要有这三个作用:
-
表现评估:模型表现如何?通过评估指标能快速了解我们在做什么
-
模型优化:模型是否适合,是否可以改进?哪种模型最接近我们的数据点?
-
统计决策:模型是否足以让我们使用?这个模型通过我们严格的假设检验标准了吗?
损失函数更多用于模型训练时的优化(比如梯度下降),更关注可微可导、是否为凸函数等等数学性质;评价指标更关注于是否能够反应任务需求、是否符合统计假设检验,此外评价指标也会用于模型之间的对比。
这么解释可能不严谨,但是不妨碍理解。今天的文章我们就来聊聊机器学习中的评价指标。
回归(Regression)算法指标X
-
Mean Absolute Error 平均绝对误差
-
Mean Squared Error 均方误差
-
Root Mean Squared Error 均方根误差
-
Coefficient of determination 决定系数
以下为一元变量和二元变量的线性回归示意图:
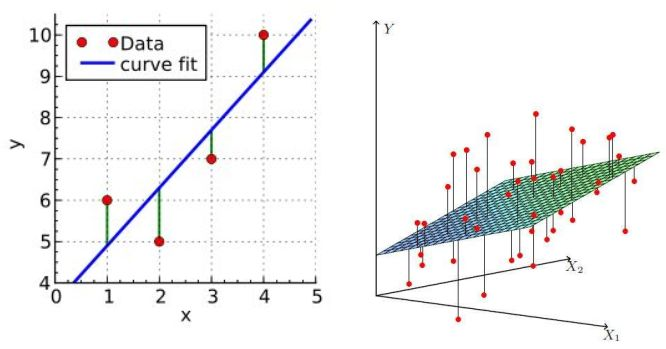
怎样来衡量回归模型的好坏呢?我们自然而然会想到采用残差(实际值与预测值差值)的均值来衡量,即:
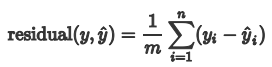
用残差的均值合理吗? 当实际值分布在拟合曲线两侧时,对于不同样本而言 有正有负,相互抵消,因此我们想到采用预测值和真实值之间的距离来衡量。
1.1 平均绝对误差
MAE平均绝对误差MAE(Mean Absolute Error)又被称为 L1范数损失。
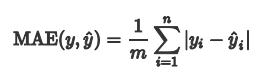
MAE有哪些不足? MAE虽能较好衡量回归模型的好坏,但是绝对值的存在导致函数不光滑,在某些点上不能求导,可以考虑将绝对值改为残差的平方,这就是均方误差。
1.2 均方误差 MSE
均方误差MSE(Mean Squared Error)又被称为 L2范数损失。
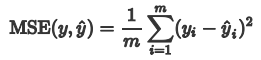
还有没有比MSE更合理一些的指标? 由于MSE与我们的目标变量的量纲不一致,为了保证量纲一致性,我们需要对MSE进行开方。
1.3 均方根误差 RMSE
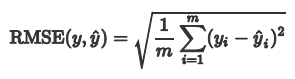
RMSE有没有不足的地方? 有没有规范化(无量纲化的指标)? 上面的几种衡量标准的取值大小与具体的应用场景有关系,很难定义统一的规则来衡量模型的好坏。比如说利用机器学习算法预测上海的房价RMSE在2000元,我们是可以接受的,但是当四五线城市的房价RMSE为2000元,我们还可以接受吗?下面介绍的决定系数就是一个无量纲化的指标。
1.4 决定系数
决定系数又称为 score,反映因变量的全部变异能通过回归关系被自变量解释的比例。
变量之所以有价值,就是因为变量是变化的。什么意思呢?比如说一组因变量为[0, 0, 0, 0, 0],显然该因变量的结果是一个常数 0,我们也没有必要建模对该因变量进行预测。假如一组的因变量为[1, 3, 7, 10, 12],该因变量是变化的,也就是有变异,因此需要通过建立回归模型进行预测。这里的变异可以理解为一组数据的方差不为 0。

-
如果结果是0,就说明模型预测不能预测因变量。
-
如果结果是1,就说明是函数关系。
-
如果结果是0-1之间的数,就是我们模型的好坏程度。
化简上面的公式,分子就变成了我们的均方误差MSE,下面分母就变成了方差:
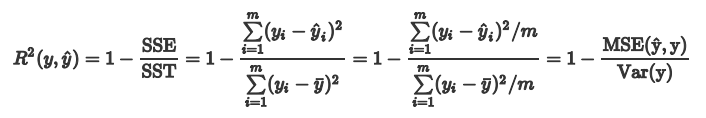
以上评估指标有没有缺陷,如果有,该怎样改进? 以上的评估指标是基于误差的均值对进行评估的,均值对异常点(outliers)较敏感,如果样本中有一些异常值出现,会对以上指标的值有较大影响,即均值是非鲁棒的。
1.5 解决评估指标鲁棒性问题
我们通常用以下两种方法解决评估指标的鲁棒性问题:鲁棒性也就是健壮和强壮的意思。它也是在异常和危险情况下系统生存的能力
-
剔除异常值,设定一个相对误差,当该值超过一定的阈值时,则认为其是一个异常点,剔除这个异常点,将异常点剔除之后。再计算平均误差来对模型进行评价。
-
使用误差的分位数来代替,如利用中位数来代替平均数。
分类(Classification)算法指标
-
混淆矩阵 Confusion Matrix
-
准确度/精度 Accuracy
-
准确率(查准率) Precision
-
召回率(查全率)Recall
-
P-R曲线
-
Fβ Score
-
ROC
-
AUC
-
KS Kolmogorov-Smirnov
2.1 混淆矩阵 Confusion Matrix
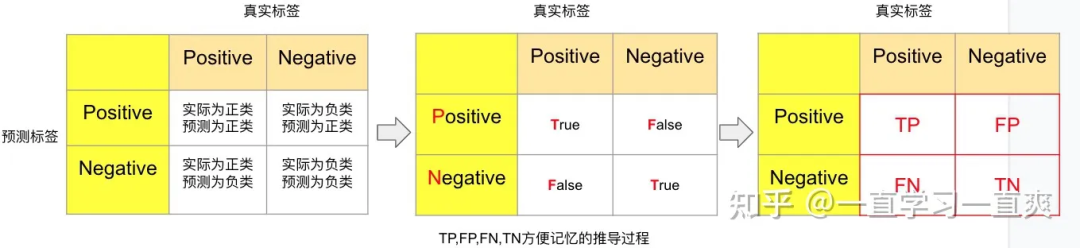
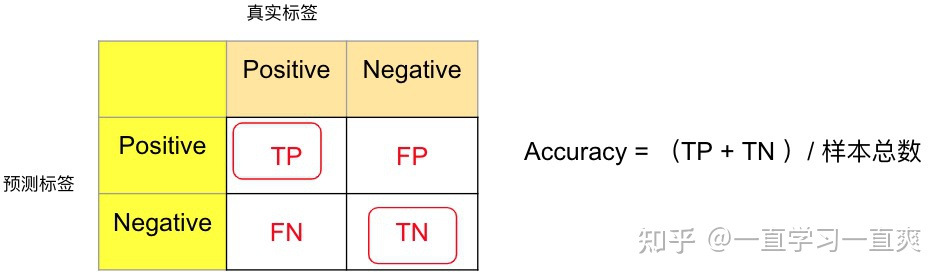
从上图的最左边的表格,可以很清楚地显示4个区域内样本的含义,沿着正对角线,可知,样本的预测标签和实际标签都是一致的,因此在第二个表格中将其标记为True,负对角线上预测标签和真实标签不一致,标记为False,在第三个表格中,结合预测标签的类别(Positive,Negative)和各个区域的True,False标记,得到了经常被搞混的4个缩写(不需要去记忆,记住上述推演过程即可):
-
True positive (TP) 真实值为 Positive,预测正确(预测值为 Positive)
-
True negative (TN) 真实值为 Negative,预测正确(预测值为 Negative)
-
False positive (FP) 真实值为 Negative,预测错误(预测值为 Positive),第一类错误, Type I error。
-
False negative (FN) 真实值为 Positive,预测错误(预测值为 Negative),第二类错误, Type II error。
2.2 准确度/准确率/精度
错误率(错误率=1-精度)和精度是分类任务重最常用的两种性能度量指标,既适用于二分类任务,也适用于多分类任务。错误率是分类错误的样本数占样本总数的比例,精度则是分类正确的样本数占样本总数的比例。
Acc 预测正确的样本的占总样本的比例,取值范围为[0,1],取值越大,模型预测能力越好。精度评价指标对平等对待每个类别,即每一个样本判对 (0) 和判错 (1) 的代价都是一样的。
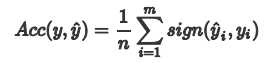
其中:
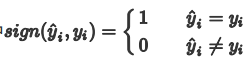
用混淆矩阵来解释Acc就是混淆矩阵中正对角线上被分类正确样本之和:正样本,模型预测也为正样本(TP) ,负样本,模型预测也为负样本(TN)。
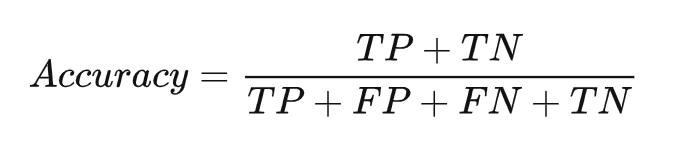
精度有什么缺陷?什么时候精度指标会失效?
-
对于有倾向性的问题,往往不能用精度指标来衡量。
-
比如,判断空中的飞行物是导弹还是其他飞行物,很显然为了减少损失,我们更倾向于相信是导弹,从而采用相应的防护措施。此时判断为导弹实际上是其他飞行物与判断为其他飞行物实际上是导弹这两种情况的重要性是不一样的。
-
对于样本类别数量严重不均衡的情况,也不能用精度指标来衡量。
-
比如,银行客户样本中好客户990个,坏客户10个。如果一个模型直接把所有客户都判断为好客户,得到精度为99%,但这显然是没有意义的。
对于以上两种情况,单纯根据Accuracy来衡量算法的优劣已经失效。这个时候就需要对目标变量的真实值和预测值做更深入的分析。
2.3 准确率(查准率) Precision
Precision 是分类器预测的正样本中预测正确的比例,取值范围为[0,1],取值越大,模型预测能力越好。
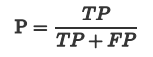
可以理解为:所有“我认为真的”中有多少是“真的”。
2.4 召回率(查全率)Recall
Recall 是分类器所预测正确的正样本占所有正样本的比例,取值范围为[0,1],取值越大,模型预测能力越好。
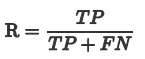
可以理解为:所有的“真的”中有多少“我认为真的”。

Precision和Recall应用场景:
-
地震的预测
对于地震的预测,我们希望的是Recall非常高,也就是说每次地震我们都希望预测出来。这个时候我们可以牺牲Precision。情愿发出1000次警报,把10次地震都预测正确了;也不要预测100次对了8次漏了2次。
“别漏报”,“宁错拿一万,不放过一个”,分类阈值较低。
-
嫌疑人定罪
基于不错怪一个好人的原则,对于嫌疑人的定罪我们希望是非常准确的。即使有时候放过了一些罪犯,但也是值得的。因此我们希望有较高的Precision值,可以合理地牺牲Recall。
“别误伤”,“宁放过一万,不错拿一个”,“疑罪从无”,分类阈值较高。
举例:某一家互联网金融公司风控部门的主要工作是利用机器模型抓取坏客户。互联网金融公司要扩大业务量,尽量多的吸引好客户,此时风控部门该怎样调整Recall和Precision? 如果公司坏账扩大,公司缩紧业务,尽可能抓住更多的坏客户,此时风控部门该怎样调整Recall和Precision?
如果互联网公司要扩大业务量,为了减少好客户的误抓率,保证吸引更多的好客户,风控部门就会提高阈值,从而提高模型的查准率Precision(“别误伤”),同时,导致查全率Recall下降。如果公司要缩紧业务,尽可能抓住更多的坏客户,风控部门就会降低阈值,从而提高模型的查全率Recall(“别漏报”),但是这样会导致一部分好客户误抓,从而降低模型的查准率 Precision。
根据以上几个案,我们知道随着阈值的变化Recall和Precision往往会向着反方向变化,这种规律很难满足我们的期望,即Recall和Precision同时增大。
有没有什么方法权衡Recall和Precision 的矛盾? 我们可以用一个指标来统一Recall和Precision的矛盾,即利用Recall和Precision的加权调和平均值作为衡量标准。
2.5 P-R曲线
Precision和Recall 是互相影响的,理想情况下肯定是做到两者都高,但是一般情况下Precision高、Recall就低, Recall高、Precision就低。
在很多情形下,我们可以根据学习模型的预测结果对样例进行排序,排在前面的是模型认为的“最可能”是正例的样本,排在最后的则是模型认为的“最不可能”是正例的样本。按此顺序逐个把样本作为正例进行预测,则每次可以计算出当前的查全率Recall和查准率Precision。以查准率为纵轴、查全率为横轴作图,就得到了查准率-查全率曲线,简称“P-R曲线”。
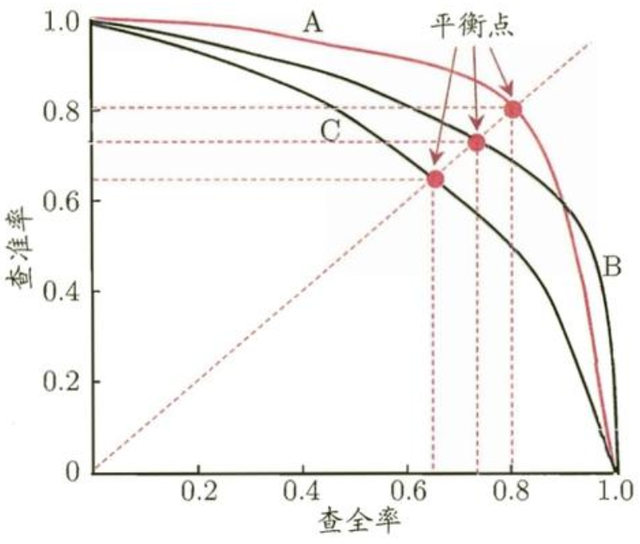
P-R曲线可以直观地显示机器学习模型在样本总体上的查全率和查准率。在进行比较时,若一个模型的P-R曲线别另外一个模型的曲线完全“包住”,则后者优于前者。例如上图中A模型性能优于C;如果两个模型的P-R曲线发生了交叉,则难以一般性地断言两者优劣,只能在具体的查准率和查全率下进行比较。
2.6 Fβ Score
在一些应用中,对查准率和查全率的重视程度不同。例如在商品推荐系统中,为了尽可能少打扰用户,更希望推荐内容的确是用户感兴趣的,此时查准率更重要;而在逃犯信息中,更希望尽可能少漏掉逃犯,此时查全率更重要。
为了均衡两个指标,我们可以采用Precision和Recall的加权调和平均(weighted harmonic mean)来衡量,即Fβ Score,Fβ能表达出对查准率/查全率的不同偏好,公式如下:
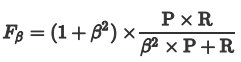
β表示权重:
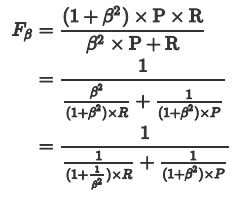
通俗的语言就是:β 越大,Recall的权重越大, β 越小,Precision的权重越大。
β=1时,退化为F1指标。
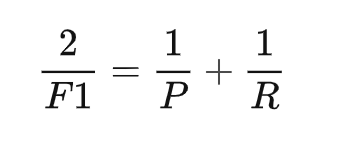
由于Fβ Score 无法直观反映数据的情况,同时业务含义相对较弱,实际工作用到的不多。
2.7 ROC 和 AUC
很多机器学习算法为测试样本产生一个实值或概率预测,然后将这个预测值与一个分类阈值(threshod)进行比较,若大于阈值则分为正类,否则为反类。
例如,神经网络在一般情形下对每个测试样本预测出一个[0.0 , 1.0]之间的实值,然后将这个值与0.5进行比较,大于0.5则判为正例,否则为反例。这个实值或概率预测结果的好坏,直接决定了机器学习模型的泛化能力。
实际上,根据这个实值或者概率预测结果,我们可以讲测试样本进行排序,“最可能”是正例的排在最前面,“最不可能”是正例的排在最后面。这样,分类过程就相当于在这个排序中以某个“截断点”(cut point)将样本分为两部分,前一部分判做正例,后一部分判做反例。
在不同的应用任务中,我们可以根据任务需求来采用不同的截断点,例如若我们更重视“查准率”,则可选择排序中考前的位置进行截断;若更重视“查全率”,则可选择靠后的位置进行截断。
因此,排序本身的质量好坏,体现了综合考虑机器学习模型在不同任务下的“期望泛化性能”的好坏,或者说“一般情况下”泛化性能的好坏。
ROC曲线(Receiver Operating Characteristic),翻译为"接受者操作特性曲线",就是从这个角度出发来研究模型泛化性能的有力工具。
2.7.1 ROC
ROC曲线为 FPR 与 TPR 之间的关系曲线,这个组合以 FPR 对 TPR,即是以代价 (costs) 对收益 (benefits),显然收益越高,代价越低,模型的性能就越好。
ROC曲线的 轴为假阳性率(FPR),即在所有的负样本中,分类器预测错误的比例。
![]()
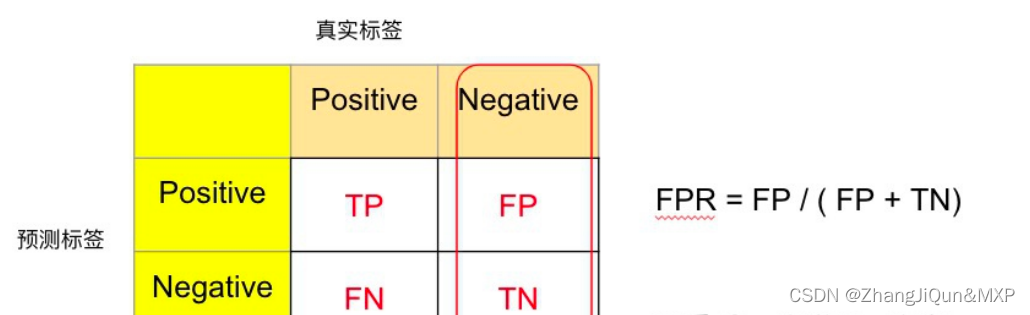
ROC曲线的 轴为真阳性率(TPR),即在所有的正样本中,分类器预测正确的比例(TPR = Recall) 。
![]()
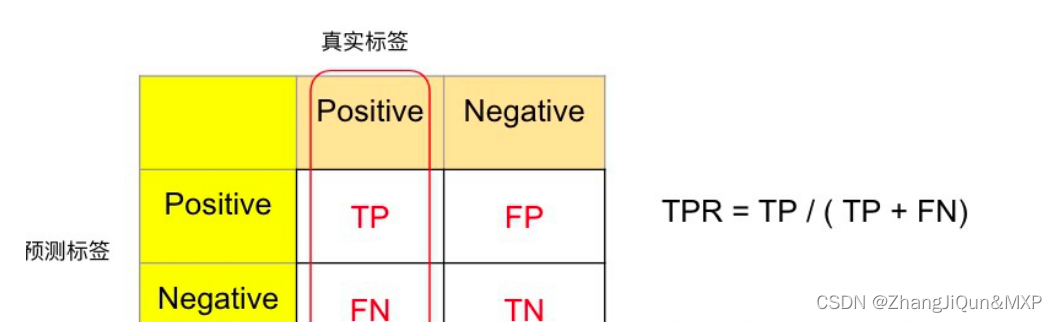
对比TPR和FPR的计算公式,我们发现其分母要么是全部的真实正类,或者全部的真实的负类,增加真实正类样本的个数,不会影响FPR的计算,反之亦然,互不干扰,因此我们常说TPR和FPR对于样本不平衡不敏感。
为了更好地理解ROC曲线,我们使用具体的实例来说明:
如在医学诊断的主要任务是尽量把生病的人群都找出来,也就是TPR越高越好。而尽量降低没病误诊为有病的人数,也就是FPR越低越好。
不难发现,这两个指标之间是相互制约的。如果某个医生对于有病的症状比较敏感,稍微的小症状都判断为有病,那么他的TPR应该会很高,但是FPR也就相应地变高。最极端的情况下,他把所有的样本都看做有病,那么TPR达到1,FPR也为1。
我们以FPR为横轴,TPR为纵轴,得到如下ROC空间:
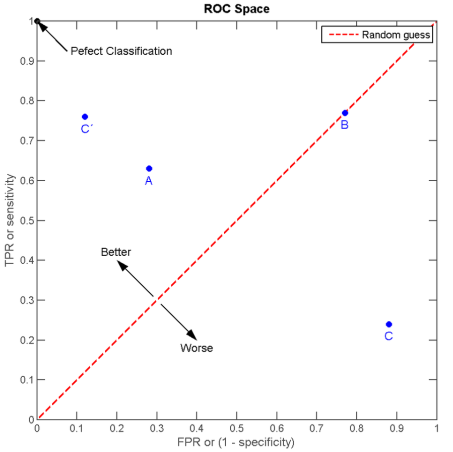
我们可以看出:
-
左上角的点(TPR=1,FPR=0),为完美分类,也就是这个医生医术高明,诊断全对;
-
点A(TPR>FPR),医生A的判断大体是正确的;
-
中线上的点B(TPR=FPR),也就是医生B全都是蒙的,蒙对一半,蒙错一半;
-
下半平面的点C(TPR<FPR),这个医生说你有病,那么你很可能没有病,医生C的话我们要反着听,为真庸医。
上图中一个阈值,得到一个点。现在我们需要一个独立于阈值的评价指标来衡量这个医生的医术如何,也就是遍历所有的阈值,得到 ROC 曲线。
假设下图是某医生的诊断统计图,为未得病人群(上图蓝色)和得病人群(下图红色)的模型输出概率分布图(横坐标表示模型输出概率,纵坐标表示概率对应的人群的数量),显然未得病人群的概率值普遍低于得病人群的输出概率值(即正常人诊断出疾病的概率小于得病人群诊断出疾病的概率)。
竖线代表阈值。显然,图中给出了某个阈值对应的混淆矩阵,通过改变不同的阈值,得到一系列的混淆矩阵,进而得到一系列的TPR和FPR,绘制出ROC曲线。
阈值为1时,不管你什么症状,医生均未诊断出疾病(预测值都为N),此时 ,位于左下。阈值为 0 时,不管你什么症状,医生都诊断结果都是得病(预测值都为P),此时,位于右上。
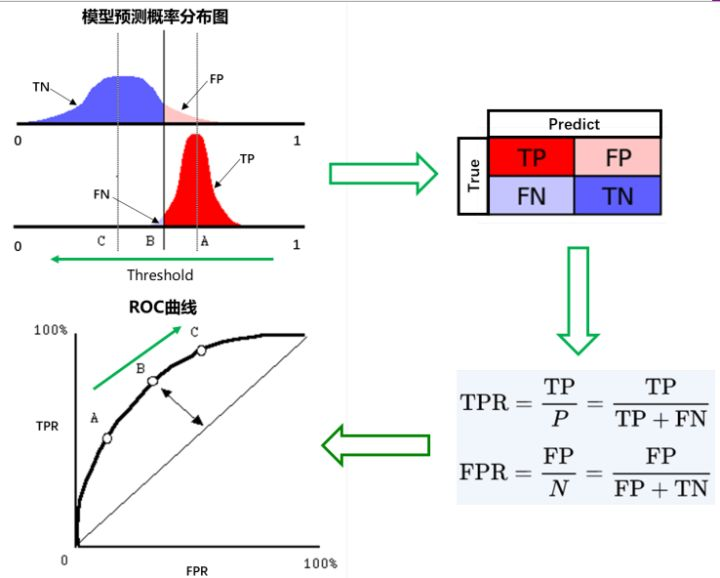
与P-R曲线类似,在进行模型比较时,如果一个模型的ROC曲线被另外一个模型的曲线完全“包住”,则可断言后者的性能优于前者;若两个模型的ROC曲线发生交叉,则难以一般性地断言两者优劣。此时如果一定要进行比较,则较为合理的判据是ROC曲线下的面积,即AUC。
2.7.2 AUC
AUC,Area Under Curve的简称,其中的Curve就是 ROC。AUC 值为 ROC 曲线所覆盖的区域面积。也就是说ROC是一条曲线,AUC是一个面积值。显然,AUC越大,分类器分类效果越好。
-
AUC = 1,是完美分类器。
-
0.5 < AUC < 1,优于随机猜测。有预测价值。
-
AUC = 0.5,跟随机猜测一样(例:丢铜板),没有预测价值。
-
AUC < 0.5,比随机猜测还差;但只要总是反预测而行,就优于随机猜测。注:对于AUC小于 0.5 的模型,我们可以考虑取反(模型预测为positive,那我们就取negtive),这样就可以保证模型的性能不可能比随机猜测差。
以下为ROC曲线和AUC值的实例:
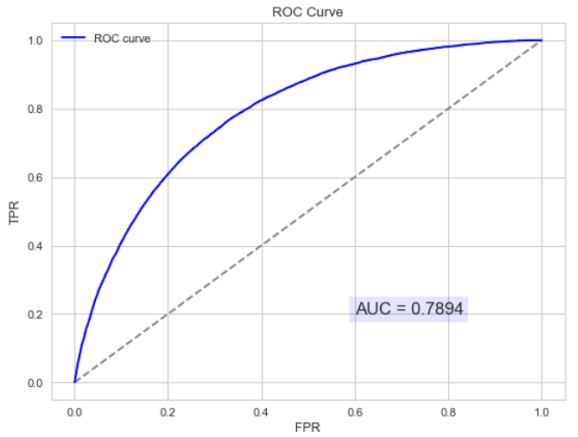
AUC的物理意义
AUC的物理意义为正样本的预测结果大于负样本的预测结果的概率。所以AUC反应的是分类器对样本的排序能力。另外值得注意的是,AUC对样本类别是否均衡并不敏感,这也是不均衡样本通常用AUC评价分类器性能的一个原因。
为什么说 ROC 和AUC都能应用于非均衡的分类问题? ROC曲线只与横坐标 (FPR) 和纵坐标 (TPR) 有关系 。我们可以发现TPR只是正样本中预测正确的概率,而FPR只是负样本中预测错误的概率,和正负样本的比例没有关系。因此 ROC 的值与实际的正负样本比例无关,因此既可以用于均衡问题,也可以用于非均衡问题。而 AUC 的几何意义为 ROC曲线下的面积,因此也和实际的正负样本比例无关。
举例:小明一家四口,小明5岁,姐姐10岁,爸爸35岁,妈妈33岁,建立一个逻辑回归分类器,来预测小明家人为成年人概率。以下为三种模型的输出结果,求三种模型的 AUC :
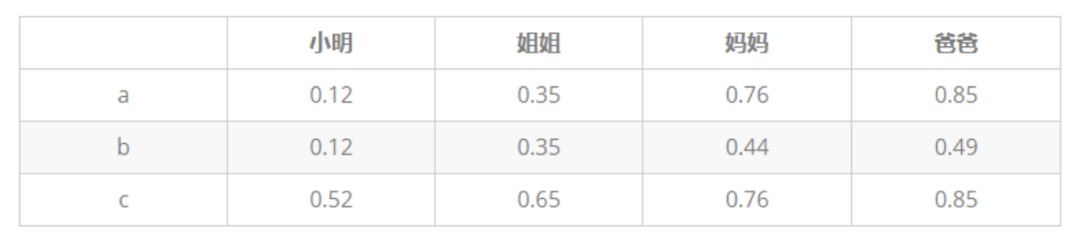
-
AUC更多的是关注对计算概率的排序,关注的是概率值的相对大小,与阈值和概率值的绝对大小没有关系。例子中并不关注小明是不是成人,而关注的是,预测为成人的概率的排序。
-
AUC只关注正负样本之间的排序,并不关心正样本内部,或者负样本内部的排序。这也体现了AUC的本质:任意个正样本的概率都大于负样本的概率的能力。
例子中AUC只需要保证(小明和姐姐)(爸爸和妈妈),小明和姐姐在前2个排序,爸爸和妈妈在后2个排序,而不会考虑小明和姐姐谁在前,或者爸爸和妈妈谁在前 。AUC只与概率的相对大小(概率排序)有关,和绝对大小没关系。由于三个模型概率排序的前两位都是未成年人(小明,姐姐),后两位都是成年人(妈妈,爸爸),因此三个模型的AUC都等于1。
以下已经对分类器输出概率从小到大进行了排列,哪些情况的AUC等于1,哪些情况的AUC为0(其中背景色表示True value,红色表示成年人,蓝色表示未成年人)。

D模型, E模型和F模型的AUC值为1,C 模型的AUC值为0(爸妈为成年人的概率小于小明和姐姐,显然这个模型预测反了)。
AUC的计算
-
法1:AUC为ROC曲线下的面积,那我们直接计算面积可得。面积为一个个小的梯形面积(曲线)之和。计算的精度与阈值的精度有关 。
-
法2:根据AUC的物理意义,我们计算正样本预测结果大于负样本预测结果的概率。取n1* n0 (n1为正样本数,n0为负样本数)个二元组,每个二元组比较正样本和负样本的预测结果,正样本预测结果高于负样本预测结果则为预测正确,预测正确的二元组占总二元组的比率就是最后得到的AUC。时间复杂度为O(N*M)。
-
法3:我们首先把所有样本按照score排序,依次用rank表示他们,如最大score的样本,rank=n (n=n0+n1,其中n0为负样本个数,n1为正样本个数),其次为n-1。那么对于正样本中rank最大的样本,rank_max,有n1-1个其他正样本比他score小,那么就有(rank_max-1)-(n1-1)个负样本比他score小。其次为(rank_second-1)-(n1-2)。最后我们得到正样本大于负样本的概率如下,其计算复杂度为O(N+M):
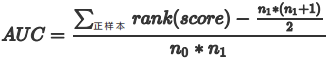
下面有一个简单的例子:
-
真实标签为 (1, 0, 0, 1, 0)
-
预测结果1(0.9, 0.3, 0.2, 0.7, 0.5)
-
预测结果2(0.9, 0.3, 0.2, 0.7, 0.8)
分别对两个预测结果进行排序,并提取他们的序号:
-
结果1 (5, 2, 1, 4, 3)
-
结果2 (5, 2, 1, 3, 4)
对正分类序号累加:
-
结果1:SUM正样本(rank(score))=5+4=9
-
结果2:SUM正样本(rank(score))=5+3=8
计算两个结果的AUC:
-
结果1:AUC= (9-2*3/2)/6=1
-
结果2:AUC= (8-2*3/2)/6=0.833
2.8 KS Kolmogorov-Smirnov
KS值是在模型中用于区分预测正负样本分隔程度的评价指标,一般应用于金融风控领域。
与ROC曲线相似,ROC是以FPR作为横坐标,TPR作为纵坐标,通过改变不同阈值,从而得到ROC曲线。
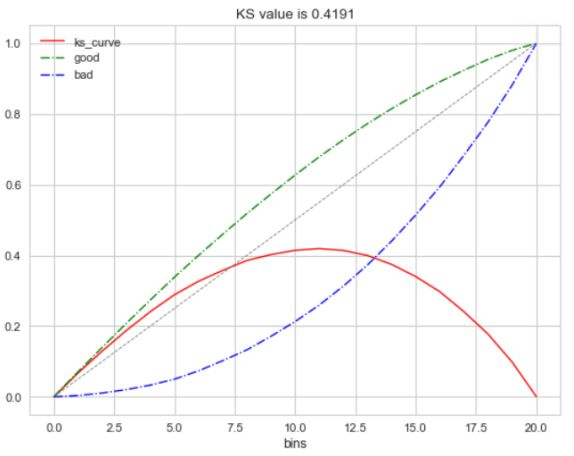
而在KS曲线中,则是以阈值作为横坐标,以FPR和TPR作为纵坐标,KS曲线则为TPR-FPR,KS曲线的最大值通常为KS值。
为什么这样求KS值呢? 我们知道,当阈值减小时,TPR和FPR会同时减小,当阈值增大时,TPR和FPR会同时增大。而在实际工程中,我们希望TPR更大一些,FPR更小一些,即TPR-FPR越大越好,即KS值越大越好。
可以理解TPR是收益,FPR是代价,KS值是收益最大。图中绿色线是TPR、蓝色线是FPR。
好了,关于机器学习常用评估指标就说到这里,在后续的学习中,我们还会遇到更多的指标,到时候我们再一一解释。相信大家已经有些云里雾里了,尤其是关于混淆矩阵和ROC&AUC。可以反复多看几遍,慢慢体会,也推荐看看周志华老师《机器学习》西瓜书里关于这一部分的描述。