目录
- 题目描述:108. 将有序数组转换为二叉搜索树(简单)
- 题目接口
- 解题思路
- 代码
- PS:
题目描述:108. 将有序数组转换为二叉搜索树(简单)
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 高度平衡 二叉搜索树。
高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。
LeetCode做题链接:LeetCode-两数之和
示例 1:
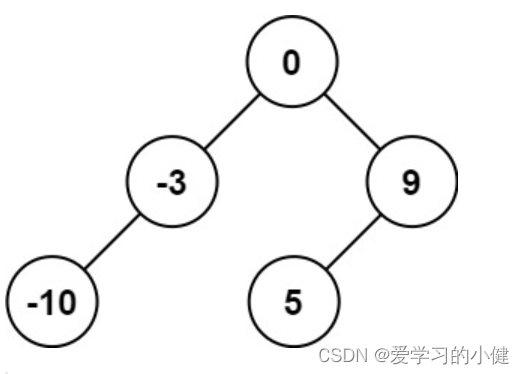
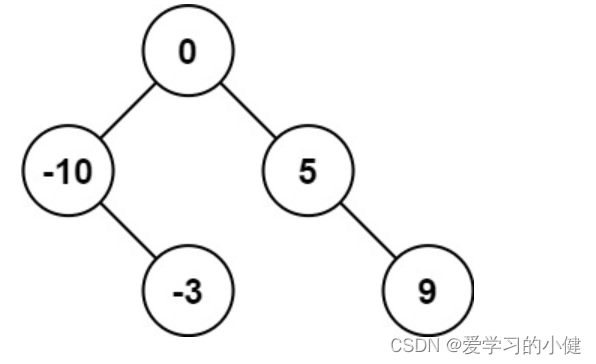
输入:nums = [-10,-3,0,5,9]
输出:[0,-3,9,-10,null,5]
解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案:
示例 2:
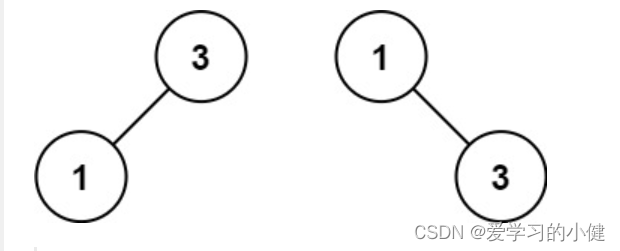
输入:nums = [1,3]
输出:[3,1]
解释:[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。
提示:
1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 按 严格递增 顺序排列
题目接口
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public TreeNode sortedArrayToBST(int[] nums) {}
}
解题思路
- 定义一个
TreeNode类,表示二叉树的节点。每个节点包含一个整数值和左右子节点的引用。 - 在
sortedArrayToBST方法中,调用dfs方法来递归地构建平衡二叉搜索树。dfs方法接受三个参数:整数数组nums、子数组的起始索引lo和结束索引hi。 - 在
dfs方法中,首先检查当前子数组是否为空(即lo > hi),如果是,则返回null表示没有节点需要构造。 - 如果当前子数组不为空,计算当前子数组的中间索引
mid,然后创建一个值为nums[mid]的根节点。 - 接下来,递归地构建左子树和右子树。左子树的范围是
[lo, mid-1],右子树的范围是[mid+1, hi]。通过传递新的起始索引和结束索引给dfs方法来实现递归。 - 最后,返回当前子数组的根节点。
- 当所有子数组都被处理后,
sortedArrayToBST方法将返回最终构建的平衡二叉搜索树的根节点。
代码
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
public TreeNode sortedArrayToBST(int[] nums) {return dfs(nums, 0, nums.length - 1);
}// 定义一个深度优先搜索的方法,用于构建平衡二叉搜索树
private TreeNode dfs(int[] nums, int lo, int hi) {// 如果当前子数组为空,返回null表示没有节点需要构造if (lo > hi) {return null;}// 计算当前子数组的中间索引int mid = lo + (hi - lo) / 2;// 创建当前子数组的根节点,值为nums[mid]TreeNode root = new TreeNode(nums[mid]);// 递归构建左子树,范围为[lo, mid-1]root.left = dfs(nums, lo, mid - 1);// 递归构建右子树,范围为[mid+1, hi]root.right = dfs(nums, mid + 1, hi);// 返回当前子数组的根节点return root;
}成功!
PS:
感谢您的阅读!如果您觉得本篇文章对您有所帮助,请给予博主一个赞喔~

![[C#][原创]操作注册表一些注意点](https://img-blog.csdnimg.cn/img_convert/a27162d9b3fbbcd63bf659c7d9645a5f.gif)