1. 从混合高斯分布中采样

Example 1: Mixture of Gaussian distribution

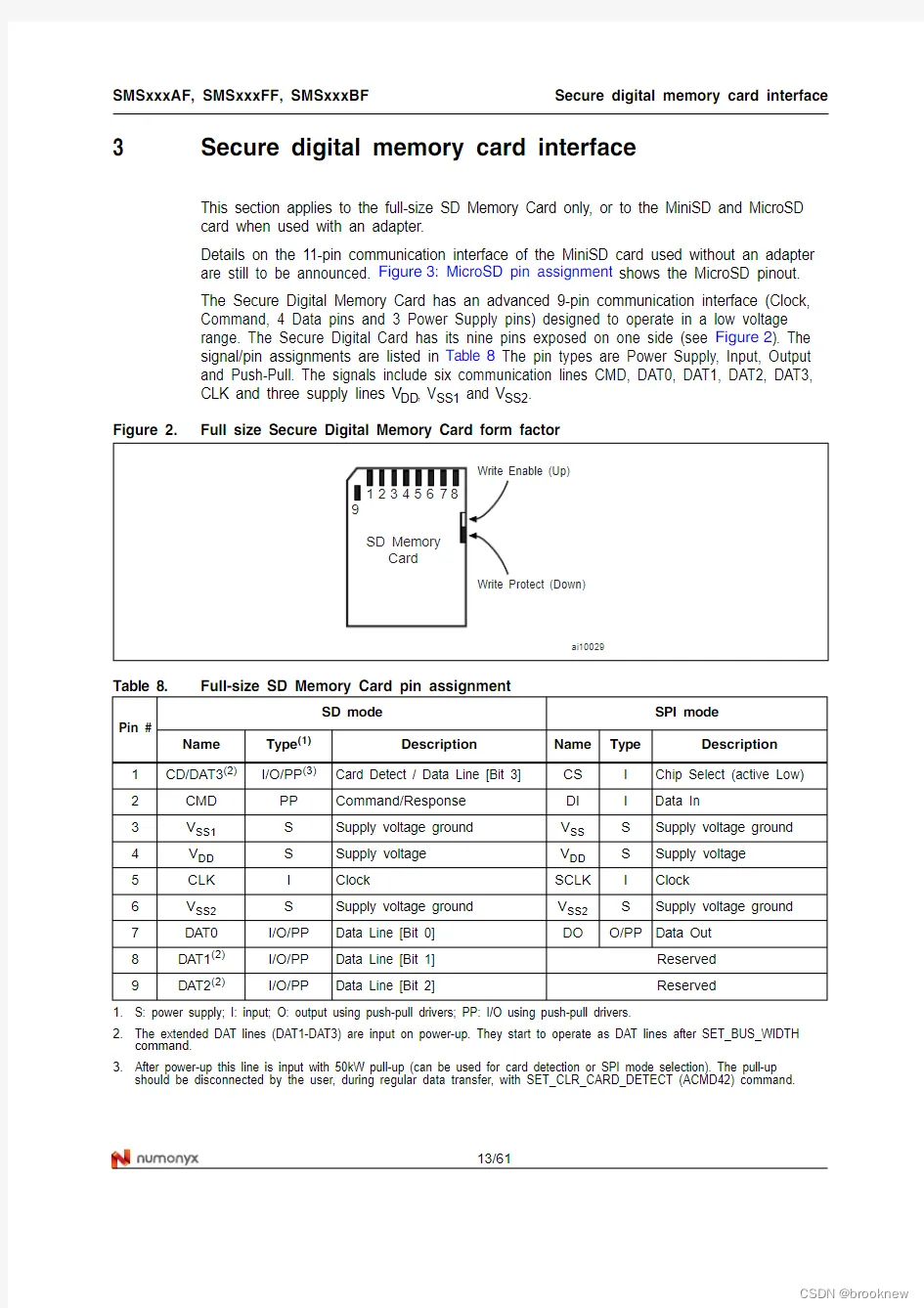
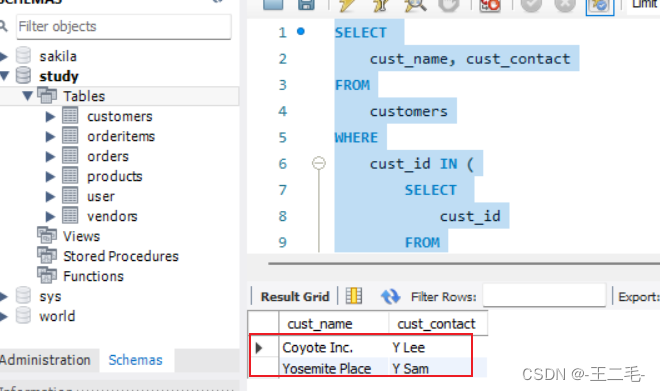
Let $X_1\sim N\left({\mu }_1,{\sigma }_1^2\right),X_2\sim N\left({\mu }_2,{\sigma }_2^2\right)$ with ${\sigma }_1>0$ and ${\sigma }_2>0$, and let $X_1$ and $X_2$ be independent. Let $\Theta \sim \mathrm{Ber}(p)$ with $p\in (0,1)$ and let $\Theta$ be independent of $X_1$ and $X_2$. Then, $(\Theta )X_1+(1-\Theta )X_2$ is a simplest Gaussian mixture model.\

Assignment: $\Theta X_1+(1-\Theta )X_2$ has a probability density
$$\frac{p}{\sqrt{2\pi }{\sigma }_1}\exp \left(-\frac{{\left(x-{\mu }_1\right)}^2}{2{\sigma }_1^2}\right)+\frac{1-p}{\sqrt{2\pi }{\sigma }_2}\exp \left(-\frac{{\left(x-{\mu }_2\right)}^2}{2{\sigma }_2^2}\right)\text{. }$$
(Hint: $P\left(\Theta X_1+(1-\Theta )X_2⩽x\right)=P\left(X_1⩽x\mid \Theta =1\right)P(\Theta =1)+P\left(X_2⩽x|\Theta =0\right)P(\Theta =0)$ and the independence of $\Theta$ of $X_1$ and $X_2$.)

2. Python编程

2.1. 伪代码

We now aim to sample a random quantity from the distribution of the above Gaussian Mixture Model.
Pseudo-code

• Sample a random quantity $\Theta \sim \mathrm{Ber}(p)$
• • If $\Theta =1$, sample a random quantity $X\sim N\left({\mu }_1,{\sigma }_1^2\right)$,
• • If $\Theta =0$, sample a random quantity $X\sim N\left({\mu }_2,{\sigma }_2{}^2\right)$.
• Return $Y=X$.

2.2. Python编程实现

Assignment: Realize the above psendocode by programming to create 1000 random quantities, and draw a histogram. (Hint: To draw a random quantity $X$ from $N\left(\mu ,{\sigma }^2\right)$, first draw a random quantity $Z\sim N(0,1)$ and take $X=\mu +\sigma Z$.)\

import numpy as np
import matplotlib.pyplot as plt
# Parameters for the mixture distribution
p = 0.7
mu1, sigma1 = 5, 2
mu2, sigma2 = 10, 3# Generate random quantities
theta = np.random.choice([0, 1], size=1000, p=[1 - p, p])
X = np.zeros(1000)for i in range(1000):if theta[i] == 1:X[i] = np.random.normal(mu1, sigma1)else:X[i] = np.random.normal(mu2, sigma2)# Plot histogram
plt.hist(X, bins=30, density=True, alpha=0.6, color='g', label='Sampled Data')
plt.xlabel('Value')
plt.ylabel('Density')
plt.title('Histogram of Mixture of Gaussian Distribution')
plt.legend()
plt.grid(True)
plt.show()