一、卷积神经网络(CNN)原理

1.1 卷积神经网络的组成

• 定义
  • 卷积神经网络由一个或多个卷积层、池化层以及全连接层等组成。与其他深度学习结构相比，卷积神经网络在图像等方面能够给出更好的结果。这一模型也可以使用反向传播算法进行训练。相比较其他浅层或深度神经网络，卷积神经网络需要考量的参数更少，使之成为一种颇具吸引力的深度学习结构。

我们来看一下卷积网络的整体结构什么样子。

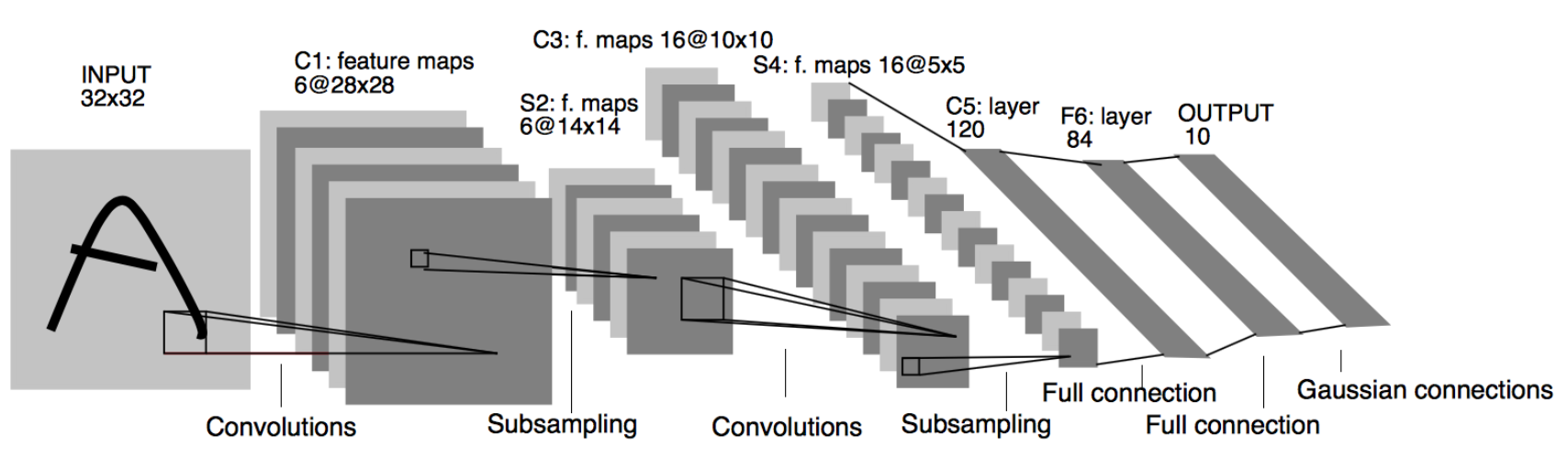
1、32*32图片做一次卷积 变成 6 张图（分别用6个7*7的卷积核同时操作）

2、subsampling   池化，将图片缩小到原图片的一半

3、再次卷积，变成16张图片

4、subsampling   池化，将图片缩小到图片的一半

5、全连接

 其中包含了几个主要结构

• 卷积层（Convolutions）
• 池化层（Subsampling）
• 全连接层（Full connection）
• 激活函数

1.1.1 卷积层

目的

卷积运算的目的是提取输入的不同特征，某些卷积层可能只能提取一些低级的特征如边缘、线条和角等层级，更多层的网路能从低级特征中迭代提取更复杂的特征。

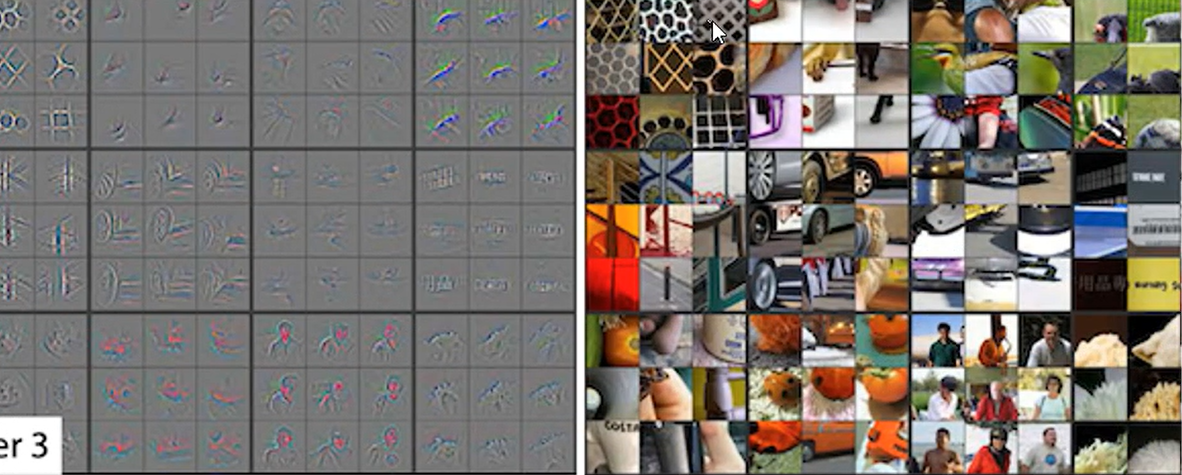
 参数 

size:卷积核/过滤器大小，选择有1 *1， 3* 3， 5 * 5（全是奇数）

padding：零填充，Valid 与Same

stride: 卷积核移动的步长，通常默认为1

计算公式 

卷积运算过程

对于之前介绍的卷积运算过程，我们用一张动图来表示更好理解些。一下计算中，假设图片长宽相等，设为N

• 一个步长，3 X 3 卷积核运算

假设是一张5 X 5 的单通道图片，通过使用3 X 3 大小的卷积核运算得到一个 3 X 3大小的运算结果（图片像素数值仅供参考）

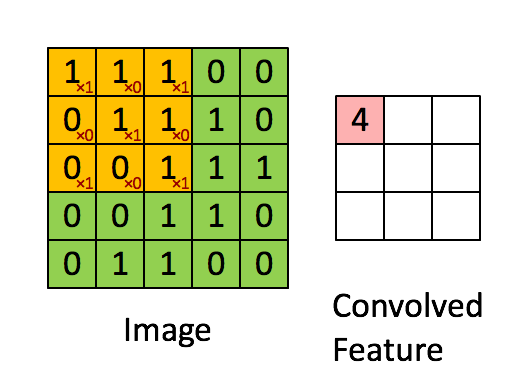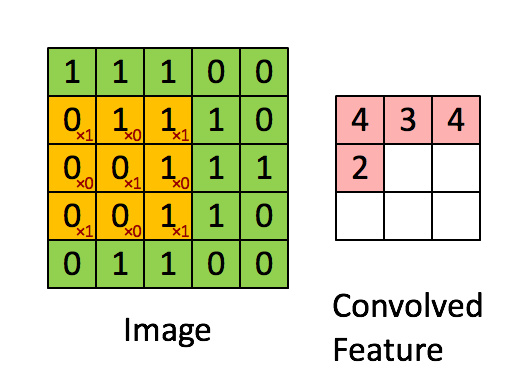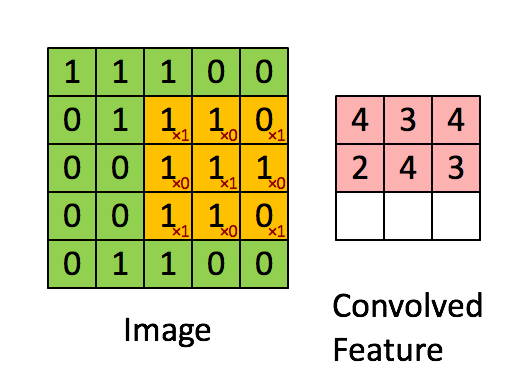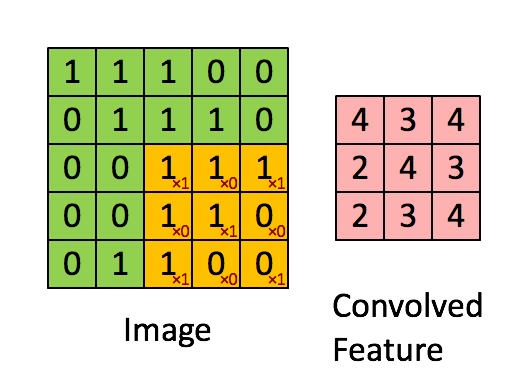
我们会发现进行卷积之后的图片变小了，假设N为图片大小，F为卷积核大小

相当于N−F+1=5−3+1=3

如果我们换一个卷积核大小或者加入很多层卷积之后，图像可能最后就变成了1 X 1 大小，这不是我们希望看到的结果。并且对于原始图片当中的边缘像素来说，只计算了一遍，对于中间的像素会有很多次过滤器与之计算，这样导致对边缘信息的丢失。

 

缺点 

• 图像变小
• 边缘信息丢失

 

针对缺点，解决办法：零填充

padding-零填充

零填充：在图片像素的最外层加上若干层0值，若一层，记做p =1。

• 为什么增加的是0？

因为0在权重乘积和运算中对最终结果不造成影响，也就避免了图片增加了额外的干扰信息。

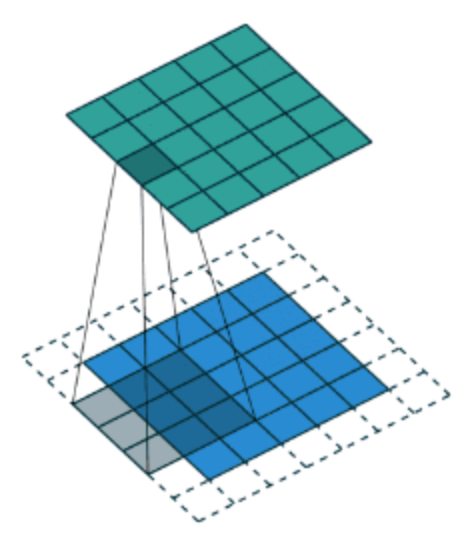
这张图中，还是移动一个像素，并且外面增加了一层0。那么最终计算结果我们可以这样用公式来计算：

  5 + 2 * p - 3 + 1 = 5

  P为1，那么最终特征结果为5。实际上我们可以填充更多的像素，假设为2层，则

  5 + 2 * 2 - 3 + 1 = 7，这样得到的观察特征大小比之前图片大小还大。所以我们对于零填充会有一些选择，该填充多少？
 

Valid and Same卷积

  有两种形式，所以为了避免上述情况，大家选择都是Same这种填充卷积计算方式

  - Valid :不填充，也就是最终大小为
    - $(N - F + 1) * (N - F + 1)$
  - Same：输出大小与原图大小一致，那么 $N$变成了$N + 2P$
    - $(N + 2P - F + 1) * (N + 2P - F + 1)$

  那也就意味着，之前大小与之后的大小一样，得出下面的等式

(N + 2P - F + 1) = N

P=(F-1)/2

  所以当知道了卷积核的大小之后，就可以得出要填充多少层像素。

奇数维度的过滤器

通过上面的式子，如果F不是奇数而是偶数个，那么最终计算结果不是一个整数，造成0.5,1.5…这种情况，这样填充不均匀，所以也就是为什么卷积核默认都去使用奇数维度大小

• 1 *1，3* 3， 5 *5，7* 7

• 另一个解释角度
  • 奇数维度的过滤器有中心，便于指出过滤器的位置

当然这个都是一些假设的原因，最终原因还是在F对于计算结果的影响。所以通常选择奇数维度的过滤器，是大家约定成俗的结果，可能也是基于大量实验奇数能得出更好的结果。

stride-步长

以上例子中我们看到的都是每次移动一个像素步长的结果，如果将这个步长修改为2,3，那结果如何？

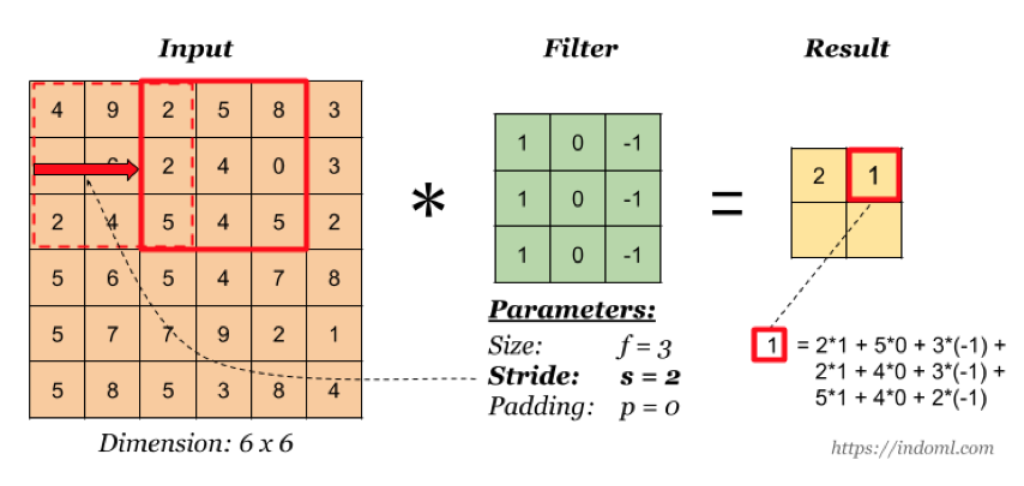
这样如果以原来的计算公式，那么结果

  N + 2P - F + 1 = 6 + 0 -3 +1 = 4

  但是移动2个像素才得出一个结果，所以公式变为

 (N+2P-F)/2 + 1 = 1.5 + 1 = 2.5，如果相除不是整数的时候，向下取整，为2。这里并没有加上零填充。

  所以最终的公式就为：

  对于输入图片大小为N，过滤器大小为F，步长为S，零填充为P，

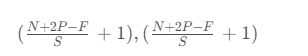
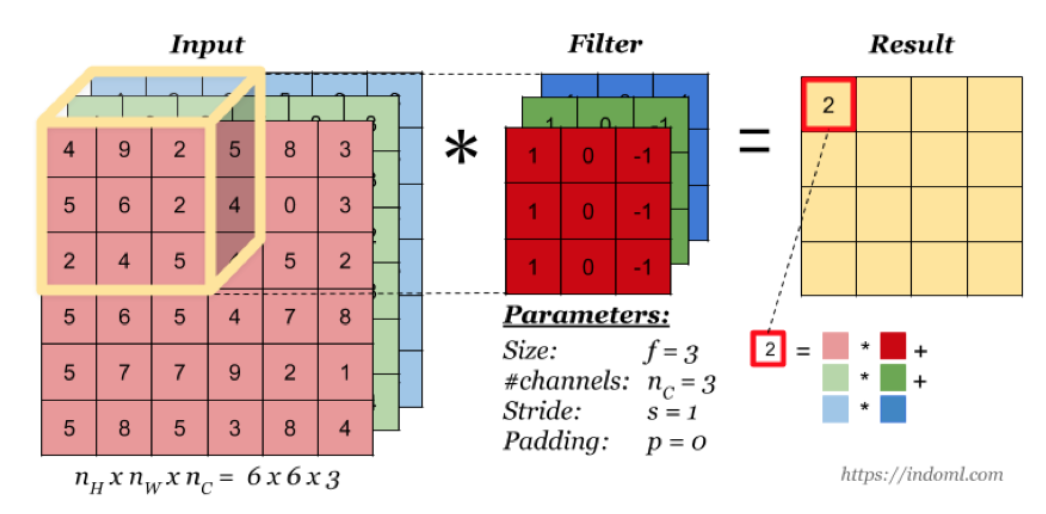
多通道卷积

当输入有多个通道（channel）时(例如图片可以有 RGB 三个通道)，卷积核需要拥有相同的channel数,每个卷积核 channel 与输入层的对应 channel 进行卷积，将每个 channel 的卷积结果按位相加得到最终的 Feature Map。

多卷积核

当有多个卷积核时，可以学习到多种不同的特征，对应产生包含多个 channel 的 Feature Map, 例如上图有两个 filter，所以 output 有两个 channel。这里的多少个卷积核也可理解为多少个神经元。

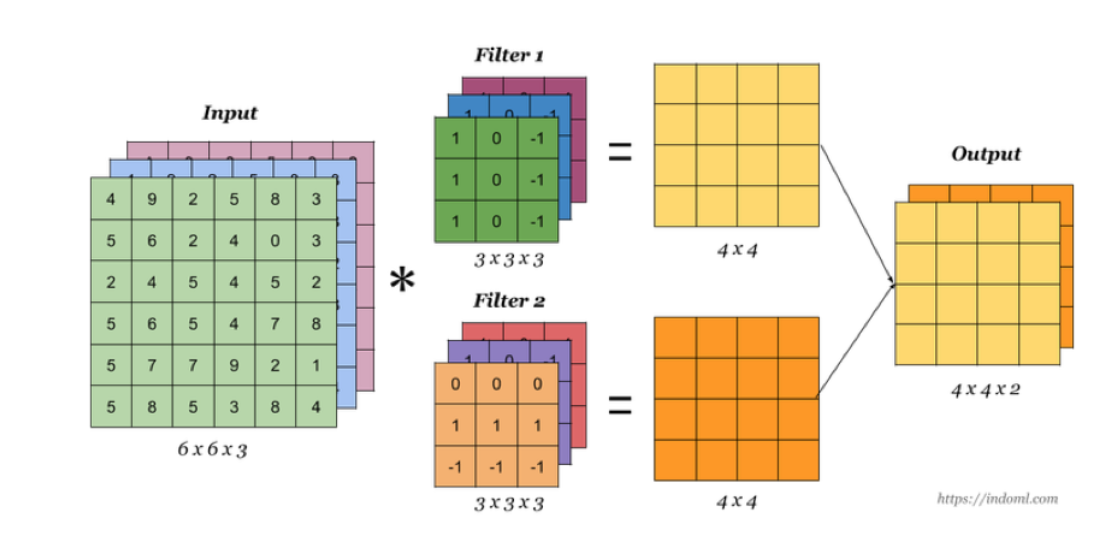
相当于我们把多个功能的卷积核的计算结果放在一起，比如水平边缘检测和垂直边缘检测器。

卷积总结

我们来通过一个例子看一下结算结果，以及参数的计算

• 假设我们有10 个Filter，每个Filter3 X 3 X 3（计算RGB图片），并且只有一层卷积，那么参数有多少？

计算：每个Filter参数个数为：3∗3∗3+1bias=28个权重参数，总共28 * 10 = 280个参数，即使图片任意大小，我们这层的参数也就这么多。

• 假设一张200 *200* 3的图片，进行刚才的Filter,步长为1，最终为了保证最后输出的大小为200 * 200，需要设置多大的零填充

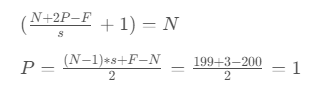
设计单个卷积Filter的计算公式

假设神经网络某层l的输入：

 所以通用的表示每一层：

池化层(Pooling)

池化层主要对卷积层学习到的特征图进行亚采样（subsampling）处理，主要由两种

• 最大池化：Max Pooling,取窗口内的最大值作为输出
• 平均池化：Avg Pooling,取窗口内的所有值的均值作为输出

意义在于：

• 降低了后续网络层的输入维度，缩减模型大小，提高计算速度
• 提高了Feature Map 的鲁棒性，防止过拟合

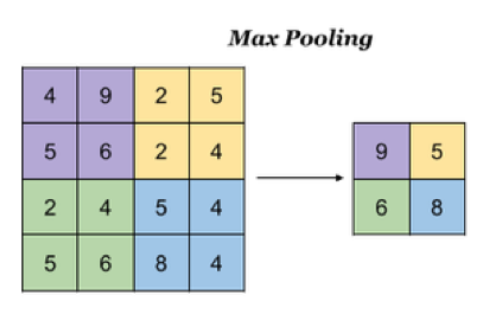
对于一个输入的图片，我们使用一个区域大小为2 *2，步长为2的参数进行求最大值操作。同样池化也有一组参数，f, s，得到2* 2的大小。当然如果我们调整这个超参数，比如说3 * 3，那么结果就不一样了，通常选择默认都是f = 2 * 2, s = 2

池化超参数特点：不需要进行学习，不像卷积通过梯度下降进行更新。

如果是平均池化则：

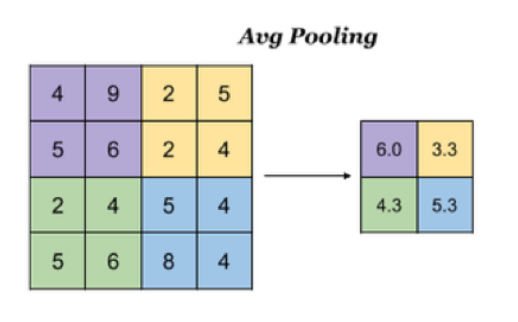
全连接层

卷积层+激活层+池化层可以看成是CNN的特征学习/特征提取层，而学习到的特征（Feature Map）最终应用于模型任务（分类、回归）：

• 先对所有 Feature Map 进行扁平化（flatten, 即 reshape 成 1 x N 向量）
• 再接一个或多个全连接层，进行模型学习

 
  -
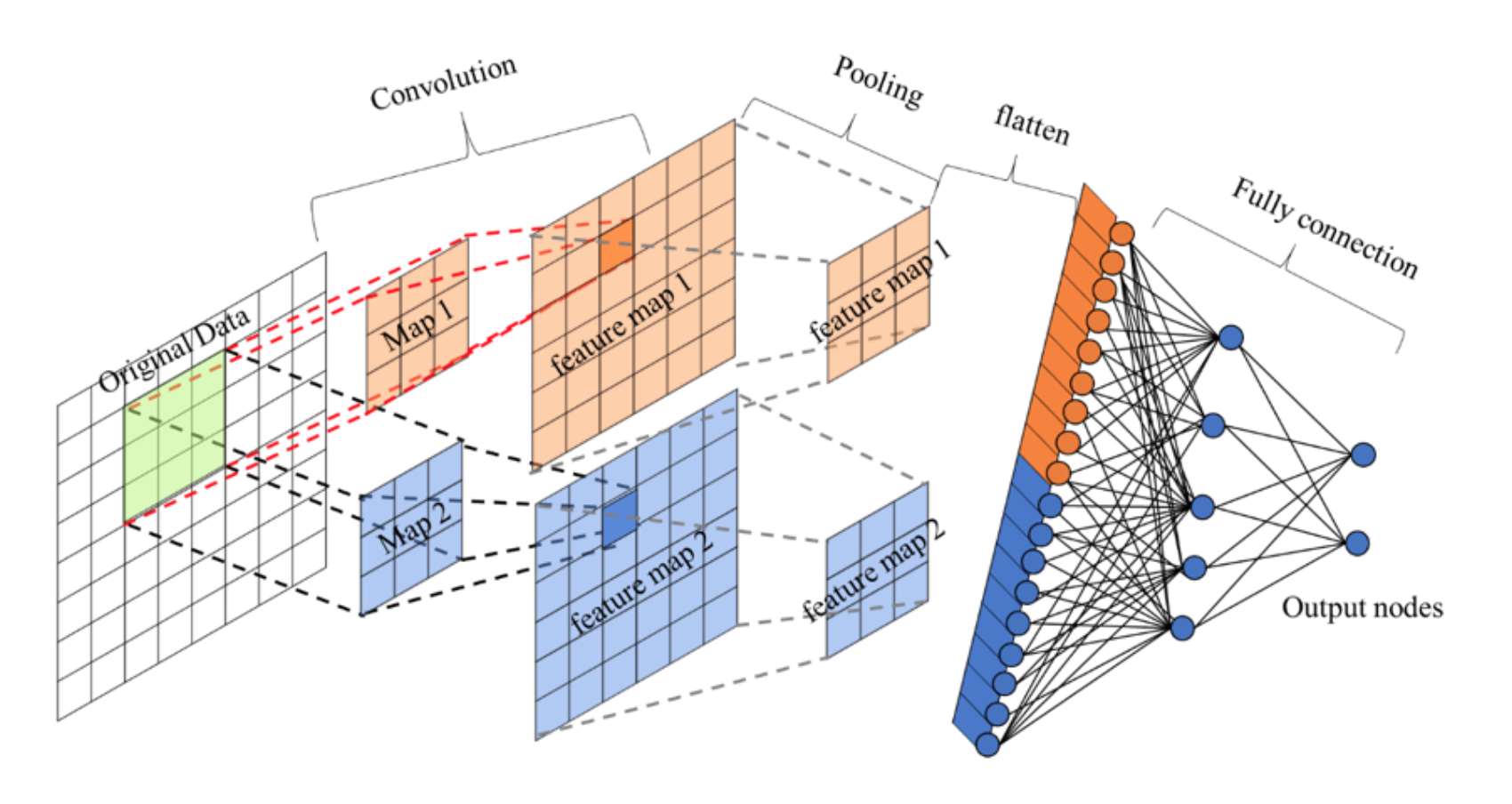
    - 卷积过滤器个数
    - 卷积过滤器大小
    - 卷积过滤器步数
    - 卷积过滤器零填充
  - 掌握池化的计算过程原理