目录
什么是 TCP 半连接队列和全连接队列?
TCP 全连接队列溢出
如何知道应用程序的 TCP 全连接队列大小?
如何模拟 TCP 全连接队列溢出的场景?
全连接队列溢出会发生什么 ?
如何增大全连接队列呢 ?
TCP 半连接队列溢出
如何查看 TCP 半连接队列长度?
如何模拟 TCP 半连接队列溢出场景?
大部分人都说 tcp_max_syn_backlog 是指定半连接队列的大小,是真的吗 ?
源码分析半连接队列的最大值是如何决定的?
TCP 第一次握手(收到 SYN 包)时会被丢弃的三种条件?
如果SYN 半连接队列已满,只能丢弃连接吗 ?
如何防御 SYN 攻击?
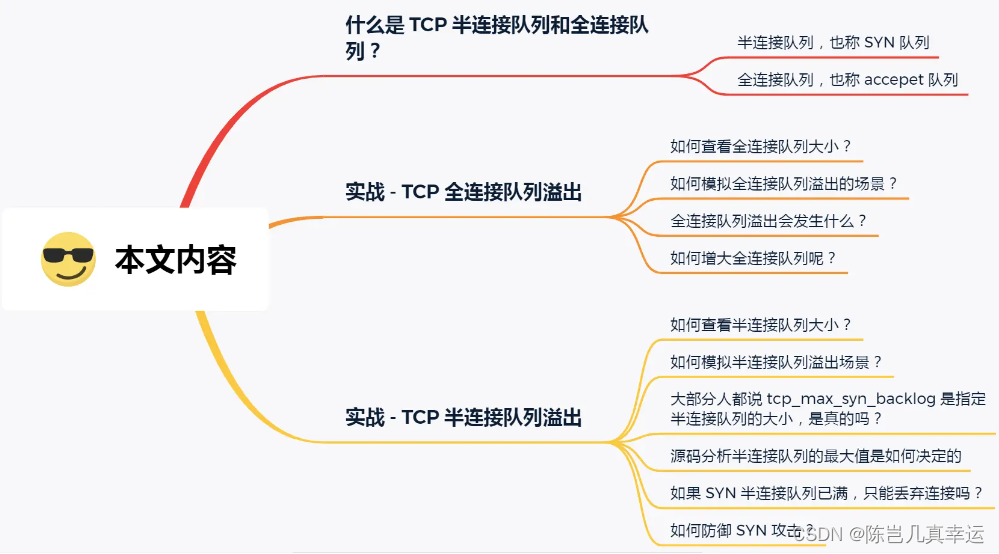
什么是 TCP 半连接队列和全连接队列?
TCP三次握手时候,Linux内核会维护两个队列:
- 半连接队列,也称 SYN 队列;
- 全连接队列,也称 accept 队列;
服务器接收到客户端SYN的时候,内核会将该连接放入半连接队列,并向客户端发送ACK+SYN,接着客户端会返回ACK,服务端收到第三次握手的ACK后,内核会把连接从半连接队列中移除,然后创建新的完全的连接,并将其添加到accept队列,等待进程调用accept函数时把连接取出来。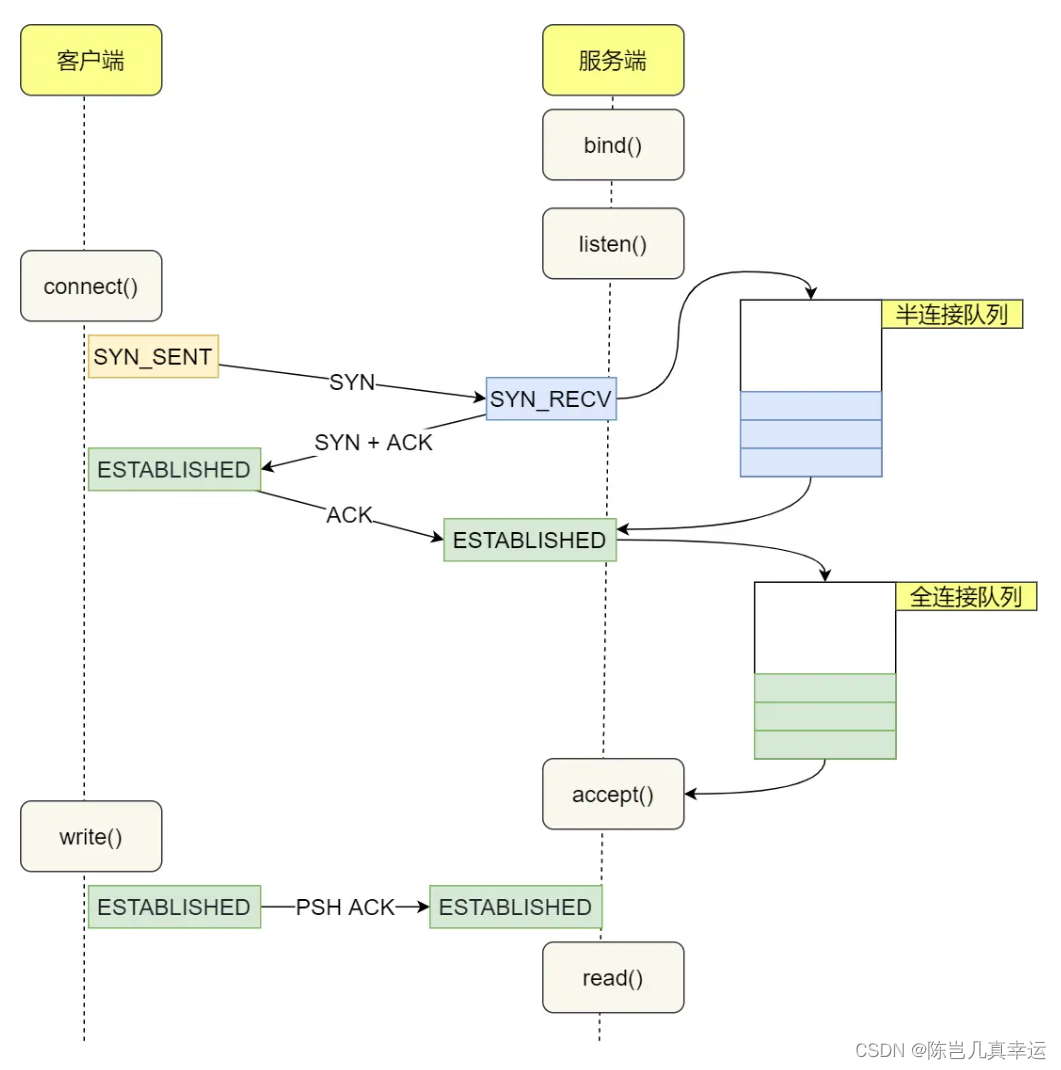
不管是半连接队列还是全连接队列,都有最大长度限制,超过限制时,内核会直接丢弃,或返回 RST 包。
TCP 全连接队列溢出
如何知道应用程序的 TCP 全连接队列大小?
$ ss -lnt
# -l 显示正在监听 ( listening ) 的 socket
# -n 不解析服务名称
# -t 只显示 tcp socket
如何模拟 TCP 全连接队列溢出的场景?
wrk工具,简单的 HTTP 压测工具,在单机多核 CPU 的条件下,使用系统自带的高性能 I/O 机制,通过多线程和事件模式,对目标机器产生大量的负载。
当服务端并发处理大量请求时,如果 TCP 全连接队列过小,就容易溢出。发生 TCP 全连接队溢出的时候,后续的请求就会被丢弃,这样就会出现服务端请求数量上不去的现象。
全连接队列溢出会发生什么 ?
Linux 有个参数可以指定当 TCP 全连接队列满了会使用什么策略来回应客户端,丢弃是默认选择,还可以选择向客户端RST复位报文,告诉客户端连接已经建立失败。
如何增大全连接队列呢 ?
TCP 全连接队列的最大值取决于 somaxconn 和 backlog 之间的最小值,也就是 min(somaxconn, backlog)。

TCP 半连接队列溢出
如何查看 TCP 半连接队列长度?
服务端处于 SYN_RECV 状态的 TCP 连接,就是 TCP 半连接队列。
如何模拟 TCP 半连接队列溢出场景?
对服务端一直发送 TCP SYN 包,但是不回第三次握手 ACK,这样就会使得服务端有大量的处于 SYN_RECV 状态的 TCP 连接。所谓的 SYN 洪泛、SYN 攻击、DDos 攻击。
大部分人都说 tcp_max_syn_backlog 是指定半连接队列的大小,是真的吗 ?
半连接队列最大值不是单单由 max_syn_backlog 决定,还跟 somaxconn 和 backlog 有关系。
源码分析半连接队列的最大值是如何决定的?
在一些系统中,半连接队列的最大值会取 somaxconn、backlog 和 max_syn_backlog 三者中的最小值,以确保在不同层面上都有适当的限制。
TCP 第一次握手(收到 SYN 包)时会被丢弃的三种条件?

如果SYN 半连接队列已满,只能丢弃连接吗 ?
开启 syncookies 功能就可以在不使用 SYN 半连接队列的情况下成功建立连接,当开启了 syncookies 功能就不会丢弃连接。
如何防御 SYN 攻击?
①:要想增大半连接队列,我们得知不能只单纯增大 tcp_max_syn_backlog 的值,还需一同增大 somaxconn 和 backlog,也就是增大全连接队列。
②:开启 tcp_syncookies 功能的方式也很简单,修改 Linux 内核参数:
③:当服务端受到 SYN 攻击时,就会有大量处于 SYN_RECV 状态的 TCP 连接,处于这个状态的 TCP 会重传 SYN+ACK ,当重传超过次数达到上限后,就会断开连接。