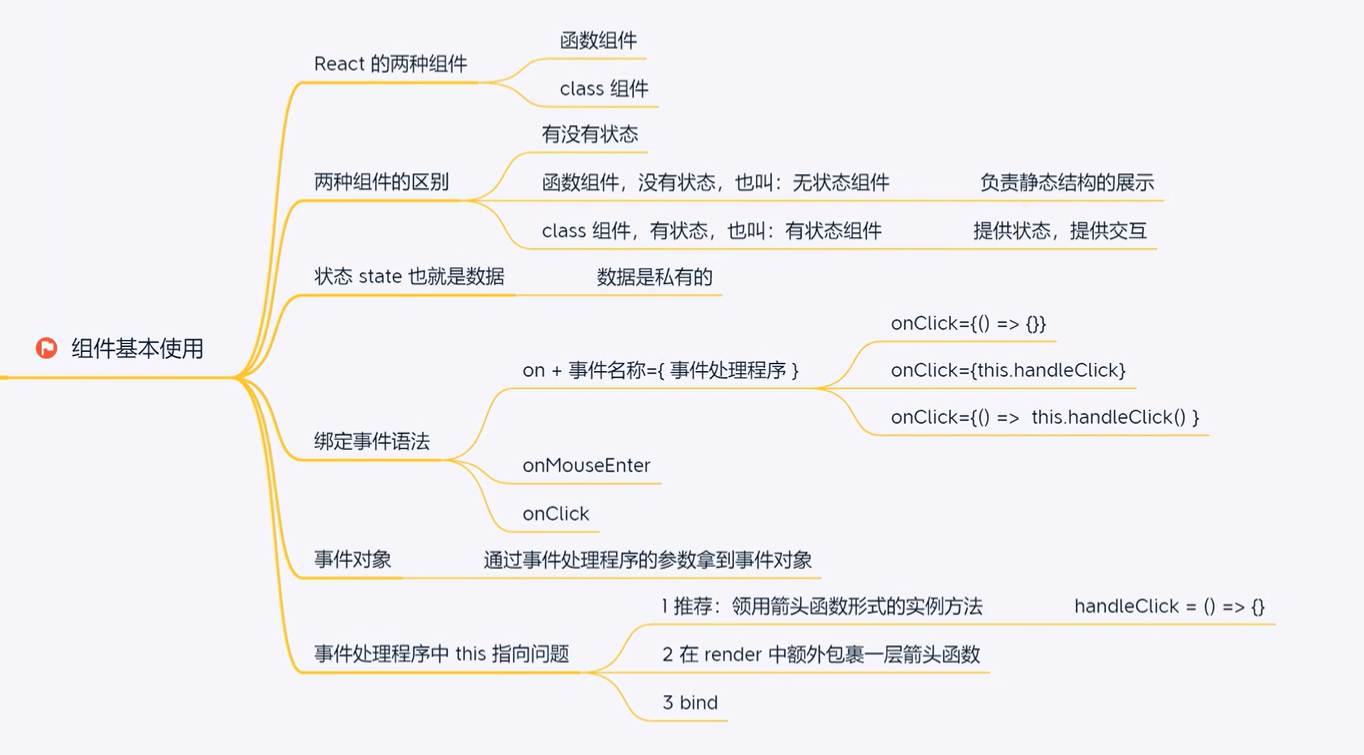
1 01背包基础
背包概述:
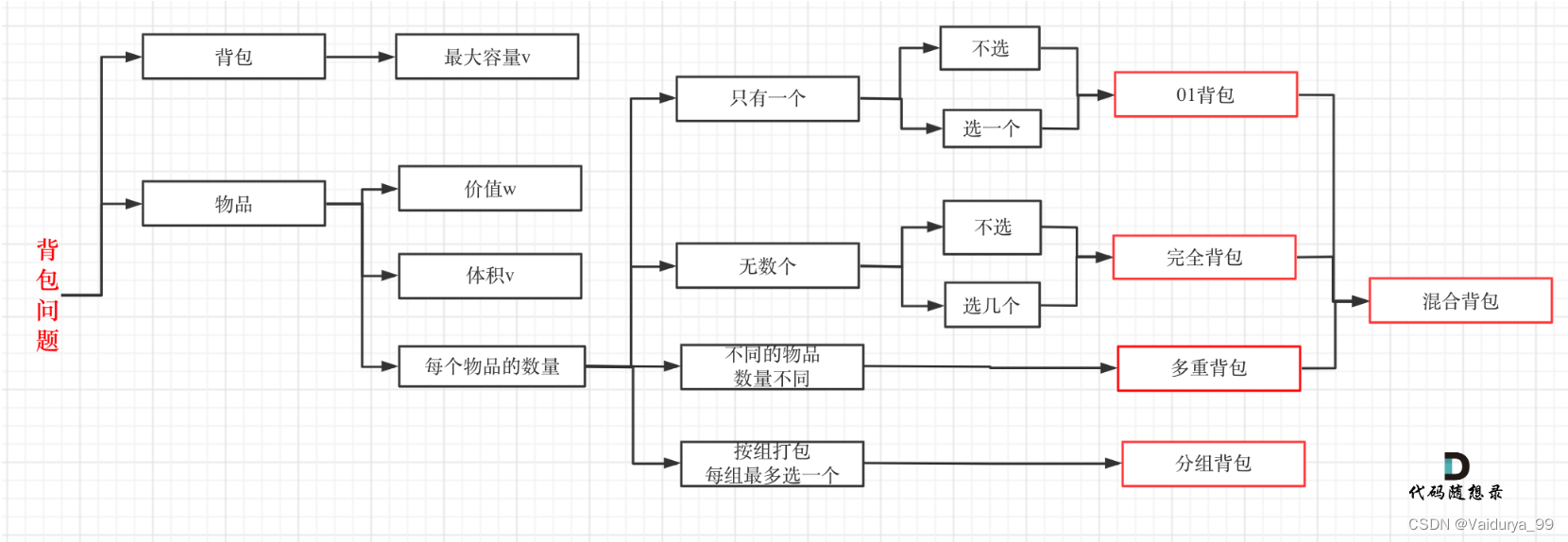
1.1 01背包是什么
有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
1.2 01背包二维数组
二维数组还比较好理解,五步法详见代码注释,AC代码:
#include<iostream>
using namespace std;const int N = 1e3 + 10;int weight[N];
int val[N];
int f[N][N]; // (i,j)表示只选取前i个商品 容积j的背包能够装的最大价值
/*if(j < weight[i])f[i][j] = f[i-1][j]; //装不下就只有不装一条路
else f[i][j] = max(f[i-1][j],f[i-1][j-weight[i]]+val[i]); //装的下就有装和不装两种选择不装i 装i第0行--f[0][j]
for(int j = 0; j <= m ; j++)
{if(j >= weight[0])f[0][j] = val[0];else f[0][j] = 0;
}
第0列—— f[i][0]全设置为0顺序:先商品i后背包j(先背包后商品也行)*/int main()
{int n,m;cin >> n >> m;for(int i = 0; i < n; i++){int tmpw,tmpval;cin >> tmpw >> tmpval;weight[i] = tmpw;val[i] = tmpval;}//初始化for(int j = 0; j <= m ; j++)if(j >= weight[0])f[0][j] = val[0];else f[0][j] = 0;for(int i = 0; i <= n; i++)f[i][0] = 0;for(int i = 1; i <= n; i++)for(int j = 1; j <= m; j++)if(j < weight[i])f[i][j] = f[i-1][j]; //装不下就只有不装一条路else f[i][j] = max(f[i-1][j],f[i-1][j-weight[i]]+val[i]); //装的下就有装和不装两种选择// for(int i = 0; i <= n; i++)// {// for(int j = 0; j <= m; j++)// {// cout << f[i][j] << ' ';// }// puts("");// }cout << f[n][m];return 0;
}1.3 01背包一维数组(滑动数组)
滑动数组实质就是利用01背包二维数组版本中每个f[i][j]只会用到上一层左侧 f[i-1][j-xx] 的数据,所以把上一层左侧数据保存在当前行的左侧,并且每次在当前行内遍历时候从右往左边遍历。AC代码:
#include<iostream>
using namespace std;const int N = 1e3 + 10;int weight[N];
int val[N];
int f[N]; // (j)表示容积j的背包能够装的最大价值/*
转换方程:
if(j < weight[i])f[j] = f[j]; //装不下就只有不装一条路
else f[j] = max(f[j],f[j-weight[i]]+val[i]); //装的下就有装和不装两种选择不装i 装i第0行--f[0] = 0;顺序:先商品i++后背包j--(j左边的作为上一层的记录),*/int main()
{int n,m;cin >> n >> m;for(int i = 0; i < n; i++){int tmpw,tmpval;cin >> tmpw >> tmpval;weight[i] = tmpw;val[i] = tmpval;}//初始化for(int i = 0; i <= n; i++)for(int j = m; j >= 0; j--)if(j < weight[i])f[j] = f[j]; //装不下就只有不装一条路else f[j] = max(f[j],f[j-weight[i]]+val[i]); //装的下就有装和不装两种选择cout << f[m];return 0;
}2 01背包应用题1——416. 分割等和子集
416. 分割等和子集
一开始看到题目,想用贪心——排序+双指针 每次都把当前相对小的放进小的sum中,写完之后发现过不了:[1,1,2,2]这样的样例。错误代码:
class Solution {
public:/*左边的sum 小于 右边的sum l++,左边的sum+=左边的sum 大于 同理如果等于左边前进 1,2,3,4, 5,6,7,8,9, 10*/bool canPartition(vector<int>& nums) {// 解法1:排序+双指针if(nums.size() == 1)return 0;sort(nums.begin(),nums.end());int l = 0;int r = nums.size() - 1;int leftsum = 0;int rightsum = 0;while(l <= r){if(leftsum <= rightsum){leftsum += nums[l++];}else{rightsum += nums[r--];}}cout << l << " " << r << endl;cout << leftsum << " " << rightsum;if(leftsum == rightsum)return 1;else return 0;}
};要明确本题中我们要使用的是01背包,因为元素我们只能用一次。
回归主题:首先,本题要求集合里能否出现总和为 sum / 2 的子集。
那么来一一对应一下本题,看看背包问题如何来解决。
只有确定了如下四点,才能把01背包问题套到本题上来。
- 背包的体积为sum / 2
- 背包要放入的商品(集合里的元素)重量为 元素的数值,价值也为元素的数值
- 背包如果正好装满,说明找到了总和为 sum / 2 的子集。
- 背包中每一个元素是不可重复放入。
具体分析过程见注释, AC代码:
class Solution {
public:// 找到一个背包 能够装nums.total(所有物体重量总和)/2的东西int dp[10005]; // 容积为i的背包 根据现有的物体重量情况最多能装的物体的重量/*转换成01背包问题:假设有一个nums.total/2的背包有若干个物体,每个物体的重量就是nums[i] 本题可以舍弃价值这个概念就是问一个nums.total/2的背包最多能够装的物体的重量是多少 能不能达到nums.total/2if(j < nums[i])dp[j] = dp[j];else dp[j] = max(dp[j] , dp[j - nums[i]]+nums[i]);dp[0] = 0;其他默认是0for物体i++ for容积j--模拟——*/bool canPartition(vector<int>& nums) {dp[0] = 0;int total = 0;for(auto i : nums)total += i;if(total % 2 == 0)total /= 2;else return 0;for(int i = 0; i < nums.size();i++){for(int j = total ; j >= 0; j--){if(j < nums[i])dp[j] = dp[j];else dp[j] = max(dp[j] , dp[j - nums[i]]+nums[i]);}}if(dp[total] == total)return 1;else return 0;}
};