手写数字识别之优化算法:观察Loss下降的情况判断合理的学习率

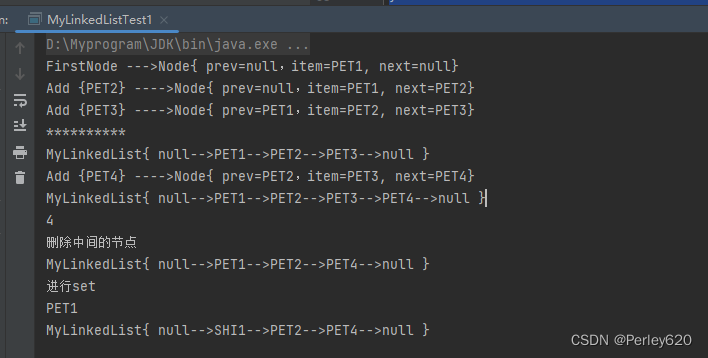
我们明确了分类任务的损失函数（优化目标）的相关概念和实现方法，本节我们依旧横向展开"横纵式"教学法，如图1 所示，本节主要探讨在手写数字识别任务中，使得损失达到最小的参数取值的实现方法。

图1：“横纵式”教学法 — 优化算法

前提条件

在优化算法之前，需要进行数据处理、设计神经网络结构，代码与上一节保持一致，如下所示。

# 加载相关库
import os
import random
import paddle
from paddle.nn import Conv2D, MaxPool2D, Linear
import numpy as np
from PIL import Image
import gzip
import json# 定义数据集读取器
def load_data(mode='train'):# 读取数据文件datafile = './work/mnist.json.gz'print('loading mnist dataset from {} ......'.format(datafile))data = json.load(gzip.open(datafile))# 读取数据集中的训练集，验证集和测试集train_set, val_set, eval_set = data# 数据集相关参数，图片高度IMG_ROWS, 图片宽度IMG_COLSIMG_ROWS = 28IMG_COLS = 28# 根据输入mode参数决定使用训练集，验证集还是测试if mode == 'train':imgs = train_set[0]labels = train_set[1]elif mode == 'valid':imgs = val_set[0]labels = val_set[1]elif mode == 'eval':imgs = eval_set[0]labels = eval_set[1]# 获得所有图像的数量imgs_length = len(imgs)# 验证图像数量和标签数量是否一致assert len(imgs) == len(labels), \"length of train_imgs({}) should be the same as train_labels({})".format(len(imgs), len(labels))index_list = list(range(imgs_length))# 读入数据时用到的batchsizeBATCHSIZE = 100# 定义数据生成器def data_generator():# 训练模式下，打乱训练数据if mode == 'train':random.shuffle(index_list)imgs_list = []labels_list = []# 按照索引读取数据for i in index_list:# 读取图像和标签，转换其尺寸和类型img = np.reshape(imgs[i], [1, IMG_ROWS, IMG_COLS]).astype('float32')label = np.reshape(labels[i], [1]).astype('int64')imgs_list.append(img) labels_list.append(label)# 如果当前数据缓存达到了batch size，就返回一个批次数据if len(imgs_list) == BATCHSIZE:yield np.array(imgs_list), np.array(labels_list)# 清空数据缓存列表imgs_list = []labels_list = []# 如果剩余数据的数目小于BATCHSIZE，# 则剩余数据一起构成一个大小为len(imgs_list)的mini-batchif len(imgs_list) > 0:yield np.array(imgs_list), np.array(labels_list)return data_generator# 定义模型结构
import paddle.nn.functional as F
# 多层卷积神经网络实现
class MNIST(paddle.nn.Layer):def __init__(self):super(MNIST, self).__init__()# 定义卷积层，输出特征通道out_channels设置为20，卷积核的大小kernel_size为5，卷积步长stride=1，padding=2self.conv1 = Conv2D(in_channels=1, out_channels=20, kernel_size=5, stride=1, padding=2)# 定义池化层，池化核的大小kernel_size为2，池化步长为2self.max_pool1 = MaxPool2D(kernel_size=2, stride=2)# 定义卷积层，输出特征通道out_channels设置为20，卷积核的大小kernel_size为5，卷积步长stride=1，padding=2self.conv2 = Conv2D(in_channels=20, out_channels=20, kernel_size=5, stride=1, padding=2)# 定义池化层，池化核的大小kernel_size为2，池化步长为2self.max_pool2 = MaxPool2D(kernel_size=2, stride=2)# 定义一层全连接层，输出维度是10self.fc = Linear(in_features=980, out_features=10)# 定义网络前向计算过程，卷积后紧接着使用池化层，最后使用全连接层计算最终输出# 卷积层激活函数使用Relu，全连接层激活函数使用softmaxdef forward(self, inputs):x = self.conv1(inputs)x = F.relu(x)x = self.max_pool1(x)x = self.conv2(x)x = F.relu(x)x = self.max_pool2(x)x = paddle.reshape(x, [x.shape[0], -1])x = self.fc(x)return x

设置学习率

在深度学习神经网络模型中，通常使用标准的随机梯度下降算法更新参数，学习率代表参数更新幅度的大小，即步长。当学习率最优时，模型的有效容量最大，最终能达到的效果最好。学习率和深度学习任务类型有关，合适的学习率往往需要大量的实验和调参经验。探索学习率最优值时需要注意如下两点：

学习率不是越小越好。学习率越小，损失函数的变化速度越慢，意味着我们需要花费更长的时间进行收敛，如图2 左图所示。
学习率不是越大越好。只根据总样本集中的一个批次计算梯度，抽样误差会导致计算出的梯度不是全局最优的方向，且存在波动。在接近最优解时，过大的学习率会导致参数在最优解附近震荡，损失难以收敛，如图2 右图所示。

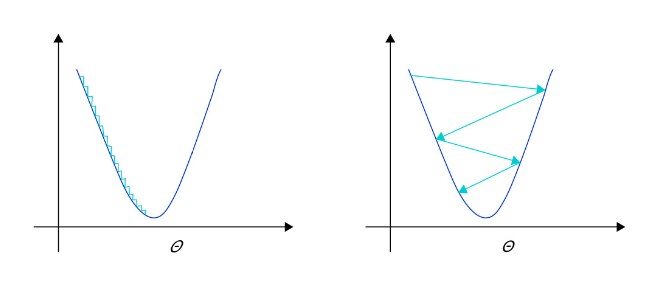
图2: 不同学习率（步长过大/过小）的示意图

在训练前，我们往往不清楚一个特定问题设置成怎样的学习率是合理的，因此在训练时可以尝试调小或调大，通过观察Loss下降的情况判断合理的学习率，设置学习率的代码如下所示。

#仅优化算法的设置有所差别
def train(model):model.train()#调用加载数据的函数train_loader = load_data('train')#设置不同初始学习率opt = paddle.optimizer.SGD(learning_rate=0.001, parameters=model.parameters())# opt = paddle.optimizer.SGD(learning_rate=0.0001, parameters=model.parameters())# opt = paddle.optimizer.SGD(learning_rate=0.01, parameters=model.parameters())EPOCH_NUM = 10for epoch_id in range(EPOCH_NUM):for batch_id, data in enumerate(train_loader()):#准备数据images, labels = dataimages = paddle.to_tensor(images)labels = paddle.to_tensor(labels)#前向计算的过程predicts = model(images)#计算损失，取一个批次样本损失的平均值loss = F.cross_entropy(predicts, labels)avg_loss = paddle.mean(loss)#每训练了100批次的数据，打印下当前Loss的情况if batch_id % 200 == 0:print("epoch: {}, batch: {}, loss is: {}".format(epoch_id, batch_id, avg_loss.numpy()))#后向传播，更新参数的过程avg_loss.backward()# 最小化loss,更新参数opt.step()# 清除梯度opt.clear_grad()#保存模型参数paddle.save(model.state_dict(), 'mnist.pdparams')#创建模型    
model = MNIST()
#启动训练过程
train(model)

学习率的主流优化算法

学习率是优化器的一个参数，调整学习率看似是一件非常麻烦的事情，需要不断的调整步长，观察训练时间和Loss的变化。经过研究员的不断的实验，当前已经形成了四种比较成熟的优化算法：SGD、Momentum、AdaGrad和Adam，效果如图3 所示。

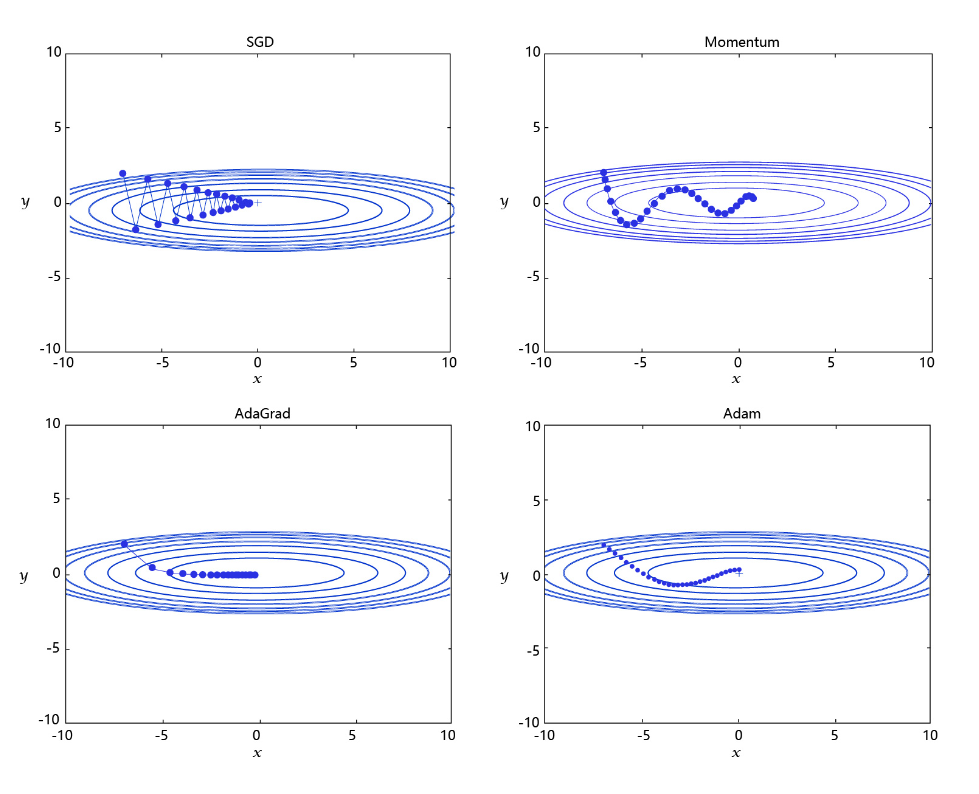
图3: 不同学习率算法效果示意图

SGD： 随机梯度下降算法，每次训练少量数据，抽样偏差导致的参数收敛过程中震荡。
Momentum： 引入物理“动量”的概念，累积速度，减少震荡，使参数更新的方向更稳定。

每个批次的数据含有抽样误差，导致梯度更新的方向波动较大。如果我们引入物理动量的概念，给梯度下降的过程加入一定的“惯性”累积，就可以减少更新路径上的震荡，即每次更新的梯度由“历史多次梯度的累积方向”和“当次梯度”加权相加得到。历史多次梯度的累积方向往往是从全局视角更正确的方向，这与“惯性”的物理概念很像，也是为何其起名为“Momentum”的原因。类似不同品牌和材质的篮球有一定的重量差别，街头篮球队中的投手（擅长中远距离投篮）喜欢稍重篮球的比例较高。一个很重要的原因是，重的篮球惯性大，更不容易受到手势的小幅变形或风吹的影响。

AdaGrad： 根据不同参数距离最优解的远近，动态调整学习率。学习率逐渐下降，依据各参数变化大小调整学习率。

通过调整学习率的实验可以发现：当某个参数的现值距离最优解较远时（表现为梯度的绝对值较大），我们期望参数更新的步长大一些，以便更快收敛到最优解。当某个参数的现值距离最优解较近时（表现为梯度的绝对值较小），我们期望参数的更新步长小一些，以便更精细的逼近最优解。类似于打高尔夫球，专业运动员第一杆开球时，通常会大力打一个远球，让球尽量落在洞口附近。当第二杆面对离洞口较近的球时，他会更轻柔而细致的推杆，避免将球打飞。与此类似，参数更新的步长应该随着优化过程逐渐减少，减少的程度与当前梯度的大小有关。根据这个思想编写的优化算法称为“AdaGrad”，Ada是Adaptive的缩写，表示“适应环境而变化”的意思。RMSProp是在AdaGrad基础上的改进，学习率随着梯度变化而适应，解决AdaGrad学习率急剧下降的问题。

Adam： 由于动量和自适应学习率两个优化思路是正交的，因此可以将两个思路结合起来，这就是当前广泛应用的算法。

说明：

每种优化算法均有更多的参数设置。理论最合理的未必在具体案例中最有效，所以模型调参是很有必要的，最优的模型配置往往是在一定“理论”和“经验”的指导下实验出来的。

我们可以尝试选择不同的优化算法训练模型，观察训练时间和损失变化的情况，代码实现如下。

#仅优化算法的设置有所差别
def train(model):model.train()#调用加载数据的函数train_loader = load_data('train')#四种优化算法的设置方案，可以逐一尝试效果opt = paddle.optimizer.SGD(learning_rate=0.01, parameters=model.parameters())# opt = paddle.optimizer.Momentum(learning_rate=0.01, momentum=0.9, parameters=model.parameters())# opt = paddle.optimizer.Adagrad(learning_rate=0.01, parameters=model.parameters())# opt = paddle.optimizer.Adam(learning_rate=0.01, parameters=model.parameters())EPOCH_NUM = 3for epoch_id in range(EPOCH_NUM):for batch_id, data in enumerate(train_loader()):#准备数据images, labels = dataimages = paddle.to_tensor(images)labels = paddle.to_tensor(labels)#前向计算的过程predicts = model(images)#计算损失，取一个批次样本损失的平均值loss = F.cross_entropy(predicts, labels)avg_loss = paddle.mean(loss)#每训练了100批次的数据，打印下当前Loss的情况if batch_id % 200 == 0:print("epoch: {}, batch: {}, loss is: {}".format(epoch_id, batch_id, avg_loss.numpy()))#后向传播，更新参数的过程avg_loss.backward()# 最小化loss,更新参数opt.step()# 清除梯度opt.clear_grad()#保存模型参数paddle.save(model.state_dict(), 'mnist.pdparams')#创建模型    
model = MNIST()
#启动训练过程
train(model)