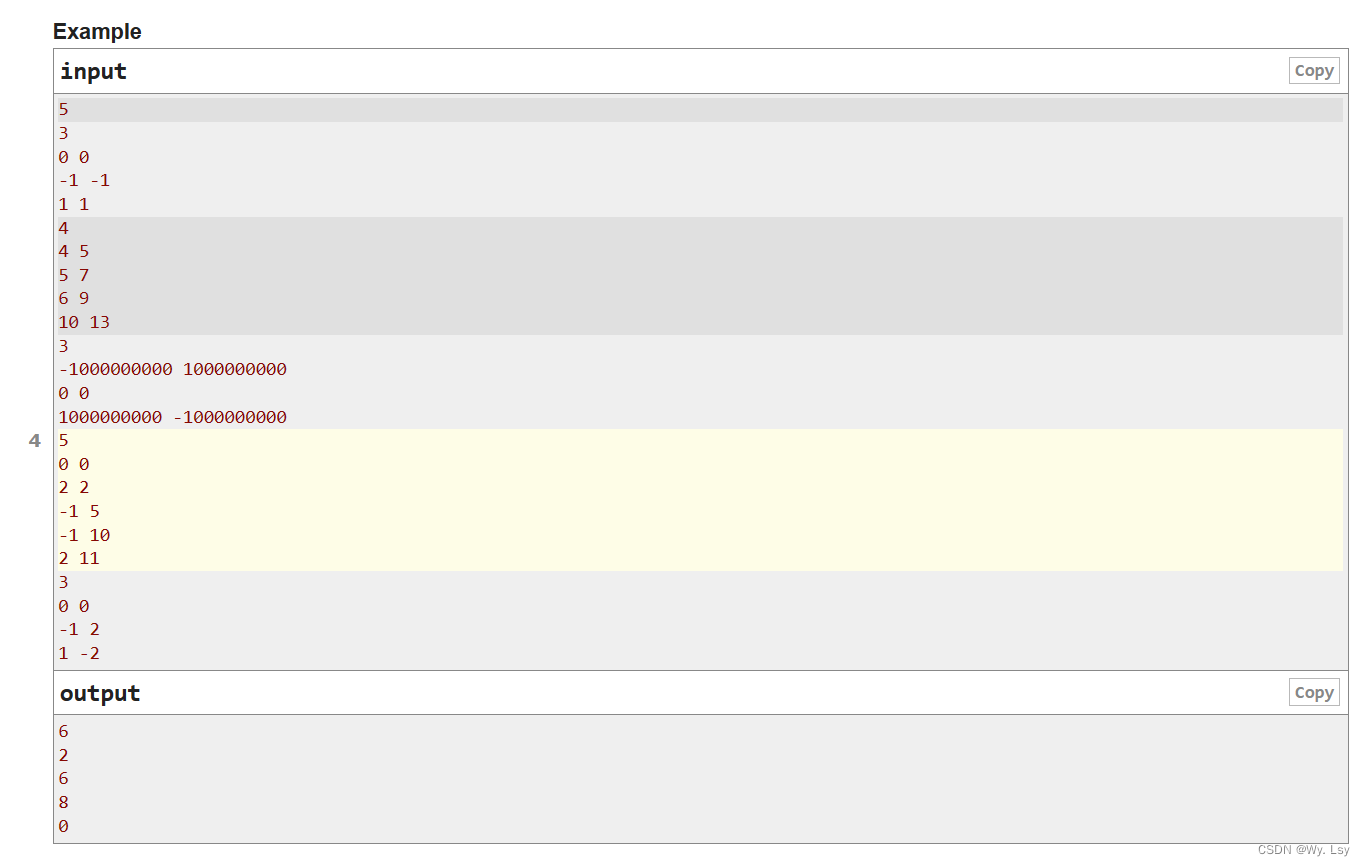
分析：

        直接暴力就会tle，不知道怎么下手，可以统计八个方向一条线上的所有坐标，这些坐标一定可以放在一起满足，分析都有哪些线，当横坐标相同时会有竖着的一条线都可以，也就是x = c，当纵坐标相同时会有横着的一条线， 也就是y = c，再看两个对角线，首先正对角线的直线方程是y = x + c，也就是满足x - y 相同的所有点都可以满足条件，再看反对角线，也就是y = -x + c，也就是x + y 相同的所有点都可以满足。

代码:

#include <bits/stdc++.h>using namespace std;
using ll = long long;int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int T;cin >> T;while(T --) {int n;cin >> n;map<ll, ll> r, c, d, ud;for(int i = 0; i < n; i ++) {ll x, y;cin >> x >> y;r[x] ++;c[y] ++;d[x - y] ++;ud[x + y] ++;}ll ans = 0;for(auto x: r) ans += x.second * (x.second - 1);for(auto x: c) ans += x.second * (x.second - 1);for(auto x: d) ans += x.second * (x.second - 1);for(auto x: ud) ans += x.second * (x.second - 1);cout << ans << '\n';}
}