目录
交叉熵
手写数字识别之损失函数
分类任务的损失函数
Softmax函数
交叉熵的简单理解:真实分布与非真实分布的交叉,完全对应,熵为0
交叉熵的代码实现
交叉熵
给定一个策略, 交叉熵就是在该策略下猜中颜色所需要的问题的期望值。更普遍的说,交叉熵用来衡量在给定的真实分布下,使用非真实分布所指定的策略消除系统的不确定性所需要付出成本的大小。
交叉的字面意思在于:真实分布与非真实分布的交叉。给定一个方案, 越优的策略, 最终的交叉熵越低。具有最低的交叉熵的策略就是最优化策略,也就是上面定义的熵。因此, 在机器学习中, 我们需要最小化交叉熵。
举例来说, 假设我有 3 枚硬币, 正正反, 记为 1,1,0. 预测结果是 0.8, 0.9, 0.3, 那么, 交叉熵的均值是:
1/3(1×log0.8+1×log0.9+(10)×log(10.3))
假设有一个完美的算法, 直接预测出了 1,1,0, 那么交叉熵的结果就是 0.
手写数字识别之损失函数
我们继续将“横纵式”教学法从横向展开,如 图1 所示,探讨损失函数的优化对模型训练效果的影响。
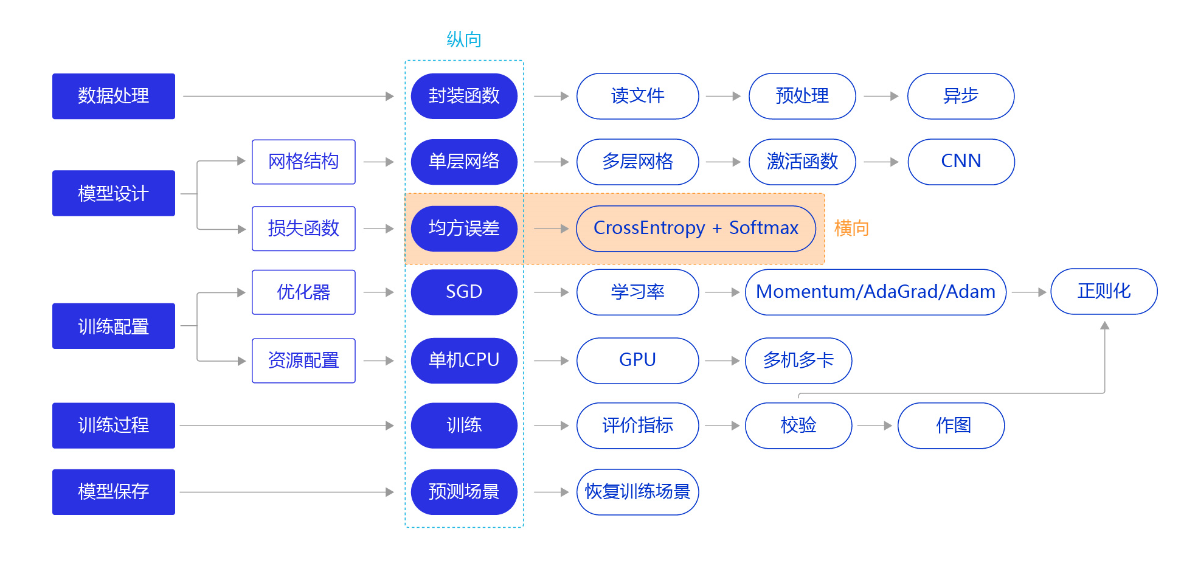
图1:“横纵式”教学法 — 损失函数优化
损失函数是模型优化的目标,用于在众多的参数取值中,识别最理想的取值。损失函数的计算在训练过程的代码中,每一轮模型训练的过程都相同,分如下三步:
- 先根据输入数据正向计算预测输出。
- 再根据预测值和真实值计算损失。
- 最后根据损失反向传播梯度并更新参数。
分类任务的损失函数
在之前的方案中,我们复用了房价预测模型的损失函数-均方误差。从预测效果来看,虽然损失不断下降,模型的预测值逐渐逼近真实值,但模型的最终效果不够理想。究其根本,不同的深度学习任务需要有各自适宜的损失函数。我们以房价预测和手写数字识别两个任务为例,详细剖析其中的缘由如下:
- 房价预测是回归任务,而手写数字识别是分类任务,使用均方误差作为分类任务的损失函数存在逻辑和效果上的缺欠。
- 房价可以是大于0的任何浮点数,而手写数字识别的输出只可能是0~9之间的10个整数,相当于一种标签。
- 在房价预测的案例中,由于房价本身是一个连续的实数值,因此以模型输出的数值和真实房价差距作为损失函数(Loss)是符合道理的。但对于分类问题,真实结果是分类标签,而模型输出是实数值,导致以两者相减作为损失不具备物理含义。
那么,什么是分类任务的合理输出呢?分类任务本质上是“某种特征组合下的分类概率”,下面以一个简单案例说明,如 图2 所示。

图2:观测数据和背后规律之间的关系
在本案例中,医生根据肿瘤大小xxx作为肿瘤性质yyy的参考判断(判断的因素有很多,肿瘤大小只是其中之一),那么我们观测到该模型判断的结果是xxx和yyy的标签(1为恶性,0为良性)。而这个数据背后的规律是不同大小的肿瘤,属于恶性肿瘤的概率。观测数据是真实规律抽样下的结果,分类模型应该拟合这个真实规律,输出属于该分类标签的概率。
Softmax函数
如果模型能输出10个标签的概率,对应真实标签的概率输出尽可能接近100%,而其他标签的概率输出尽可能接近0%,且所有输出概率之和为1。这是一种更合理的假设!与此对应,真实的标签值可以转变成一个10维度的one-hot向量,在对应数字的位置上为1,其余位置为0,比如标签“6”可以转变成[0,0,0,0,0,0,1,0,0,0]。
为了实现上述思路,需要引入Softmax函数,它可以将原始输出转变成对应标签的概率,公式如下,其中C是标签类别个数。
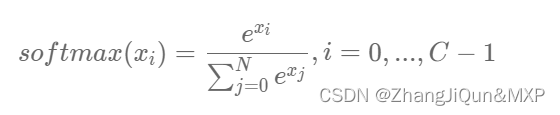
从公式的形式可见,每个输出的范围均在0~1之间,且所有输出之和等于1,这是这种变换后可被解释成概率的基本前提。对应到代码上,需要在前向计算中,对全连接网络的输出层增加一个Softmax运算,outputs = F.softmax(outputs)。
图3 是一个三个标签的分类模型(三分类)使用的Softmax输出层,从中可见原始输出的三个数字3、1、-3,经过Softmax层后转变成加和为1的三个概率值0.88、0.12、0。
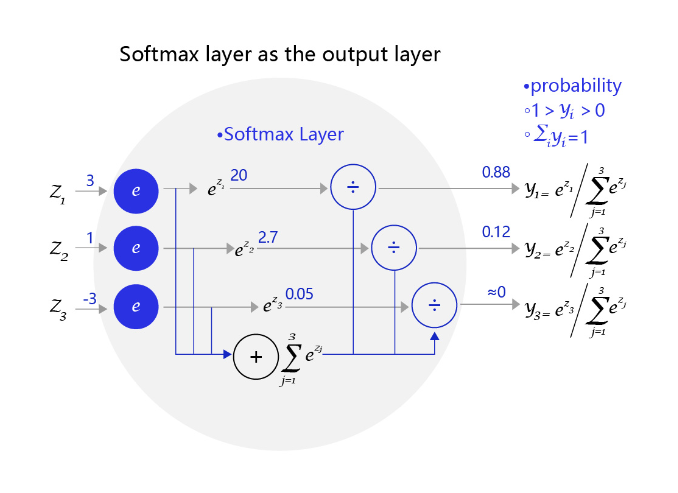
图3:网络输出层改为softmax函数
上文解释了为何让分类模型的输出拟合概率的原因,但为何偏偏用Softmax函数完成这个职能? 下面以二分类问题(只输出两个标签)进行原理的探讨。
对于二分类问题,使用两个输出接入Softmax作为输出层,等价于使用单一输出接入Sigmoid函数。如 图4 所示,利用两个标签的输出概率之和为1的条件,Softmax输出0.6和0.4两个标签概率,从数学上等价于输出一个标签的概率0.6。
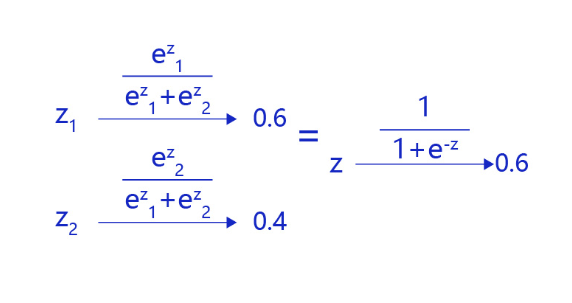
图4:对于二分类问题,等价于单一输出接入Sigmoid函数

图5 是肿瘤大小和肿瘤性质的数据图。从图中可发现,往往尺寸越大的肿瘤几乎全部是恶性,尺寸极小的肿瘤几乎全部是良性。只有在中间区域,肿瘤的恶性概率会从0逐渐到1(绿色区域),这种数据的分布是符合多数现实问题的规律。如果我们直接线性拟合,相当于红色的直线,会发现直线的纵轴0-1的区域会拉的很长,而我们期望拟合曲线0-1的区域与真实的分类边界区域重合。那么,观察下Sigmoid的曲线趋势可以满足我们对个问题的一切期望,它的概率变化会集中在一个边界区域,有助于模型提升边界区域的分辨率。
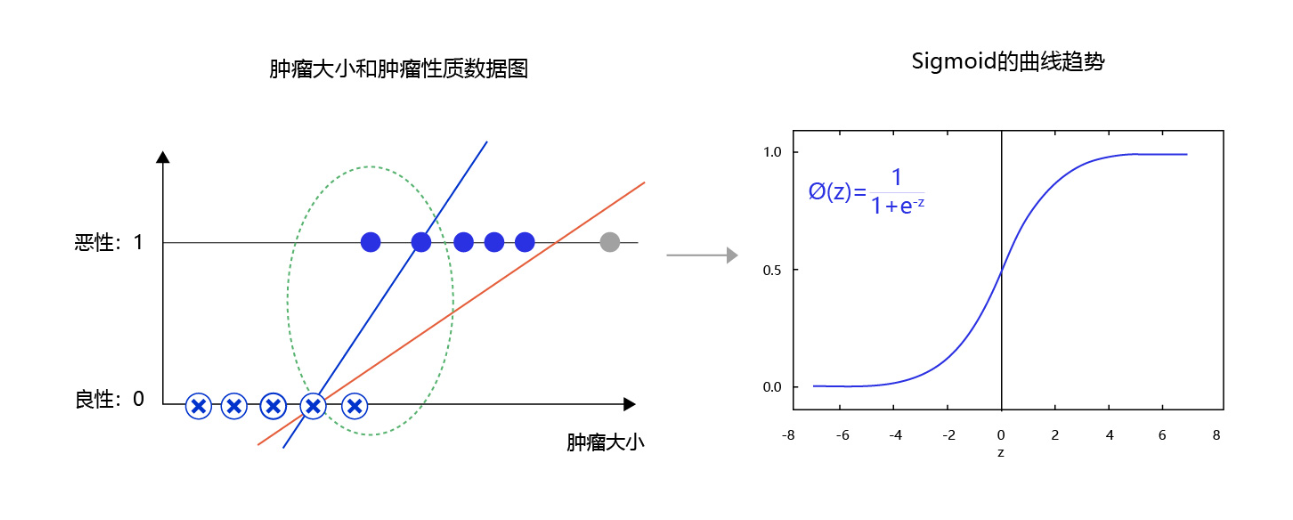
图5:使用Sigmoid拟合输出可提高分类模型对边界的分辨率
这就类似于公共区域使用的带有恒温装置的热水器温度阀门,如 图6 所示。由于人体适应的水温在34度-42度之间,我们更期望阀门的水温条件集中在这个区域,而不是在0-100度之间线性分布。
图6:热水器水温控制
交叉熵的简单理解:真实分布与非真实分布的交叉,完全对应,熵为0
假设正确标签的索引是“2”,与之对应的神经网络的输出是0.6,则交叉熵误差是−log0.6=0.51−\log 0.6 = 0.51−log0.6=0.51;若“2”对应的输出是0.1,则交叉熵误差为−log0.1=2.30−\log 0.1 = 2.30−log0.1=2.30。由此可见,交叉熵误差的值是由正确标签所对应的输出结果决定的。
交叉熵越小越好
在模型输出为分类标签的概率时,直接以标签和概率做比较也不够合理,人们更习惯使用交叉熵误差作为分类问题的损失衡量。
交叉熵损失函数的设计是基于最大似然思想:最大概率得到观察结果的假设是真的。如何理解呢?举个例子来说,如 图7 所示。有两个外形相同的盒子,甲盒中有99个白球,1个蓝球;乙盒中有99个蓝球,1个白球。一次试验取出了一个蓝球,请问这个球应该是从哪个盒子中取出的?
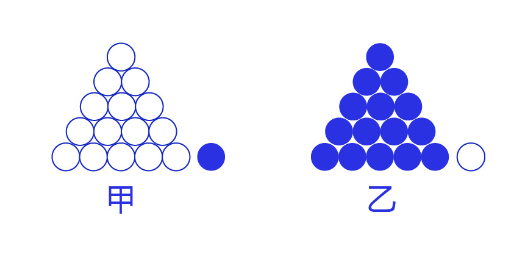
图7:体会最大似然的思想
给定一个策略, 交叉熵就是在该策略下猜中颜色所需要的问题的期望值。更普遍的说,交叉熵用来衡量在给定的真实分布下,使用非真实分布所指定的策略消除系统的不确定性所需要付出成本的大小。
交叉的字面意思在于:真实分布与非真实分布的交叉。给定一个方案, 越优的策略, 最终的交叉熵越低。具有最低的交叉熵的策略就是最优化策略,也就是上面定义的熵。因此, 在机器学习中, 我们需要最小化交叉熵。
在信息论中,交叉熵是表示两个概率分布p,q,其中p表示真实分布,q表示非真实分布,在相同的一组事件中,其中,用非真实分布q来表示某个事件发生所需要的平均比特数。从这个定义中,我们很难理解交叉熵的定义。下面举个例子来描述一下:
假设现在有一个样本集中两个概率分布p,q,其中p为真实分布,q为非真实分布。假如,按照真实分布p来衡量识别一个样本所需要的编码长度的期望为:
交叉熵可在神经网络(机器学习)中作为损失函数,p表示真实标记的分布,q则为训练后的模型的预测标记分布,交叉熵损失函数可以衡量p与q的相似性。交叉熵作为损失函数还有一个好处是使用sigmoid函数在梯度下降时能避免均方误差损失函数学习速率降低的问题,因为学习速率可以被输出的误差所控制
因此,交叉熵只计算对应着“正确解”标签的输出的自然对数。比如,假设正确标签的索引是“2”,与之对应的神经网络的输出是0.6,则交叉熵误差是−log0.6=0.51−\log 0.6 = 0.51−log0.6=0.51;若“2”对应的输出是0.1,则交叉熵误差为−log0.1=2.30−\log 0.1 = 2.30−log0.1=2.30。由此可见,交叉熵误差的值是由正确标签所对应的输出结果决定的。
交叉熵的代码实现
在手写数字识别任务中,仅改动三行代码,就可以将在现有模型的损失函数替换成交叉熵(Cross_entropy)。
- 在读取数据部分,将标签的类型设置成int,体现它是一个标签而不是实数值(飞桨框架默认将标签处理成int64)。
- 在网络定义部分,将输出层改成“输出十个标签的概率”的模式。
- 在训练过程部分,将损失函数从均方误差换成交叉熵。
在数据处理部分,需要修改标签变量Label的格式,代码如下所示。
- 从:label = np.reshape(labels[i], [1]).astype(‘float32’)
- 到:label = np.reshape(labels[i], [1]).astype(‘int64’)
#数据处理部分之前的代码,保持不变
import os
import random
import paddle
import numpy as np
import matplotlib.pyplot as plt
from PIL import Imageimport gzip
import json# 创建一个类MnistDataset,继承paddle.io.Dataset 这个类
# MnistDataset的作用和上面load_data()函数的作用相同,均是构建一个迭代器
class MnistDataset(paddle.io.Dataset):def __init__(self, mode):datafile = './work/mnist.json.gz'data = json.load(gzip.open(datafile))# 读取到的数据区分训练集,验证集,测试集train_set, val_set, eval_set = data# 数据集相关参数,图片高度IMG_ROWS, 图片宽度IMG_COLSself.IMG_ROWS = 28self.IMG_COLS = 28if mode=='train':# 获得训练数据集imgs, labels = train_set[0], train_set[1]elif mode=='valid':# 获得验证数据集imgs, labels = val_set[0], val_set[1]elif mode=='eval':# 获得测试数据集imgs, labels = eval_set[0], eval_set[1]else:raise Exception("mode can only be one of ['train', 'valid', 'eval']")# 校验数据imgs_length = len(imgs)assert len(imgs) == len(labels), \"length of train_imgs({}) should be the same as train_labels({})".format(len(imgs), len(labels))self.imgs = imgsself.labels = labelsdef __getitem__(self, idx):# img = np.array(self.imgs[idx]).astype('float32')# label = np.array(self.labels[idx]).astype('int64')img = np.reshape(self.imgs[idx], [1, self.IMG_ROWS, self.IMG_COLS]).astype('float32')label = np.reshape(self.labels[idx], [1]).astype('int64')return img, labeldef __len__(self):return len(self.imgs)
# 声明数据加载函数,使用训练模式,MnistDataset构建的迭代器每次迭代只返回batch=1的数据
train_dataset = MnistDataset(mode='train')
# 使用paddle.io.DataLoader 定义DataLoader对象用于加载Python生成器产生的数据,
# DataLoader 返回的是一个批次数据迭代器,并且是异步的;
train_loader = paddle.io.DataLoader(train_dataset, batch_size=100, shuffle=True, drop_last=True)
val_dataset = MnistDataset(mode='valid')
val_loader = paddle.io.DataLoader(val_dataset, batch_size=128,drop_last=True)
在网络定义部分,需要修改输出层结构,代码如下所示。
- 从:self.fc = Linear(in_features=980, out_features=1)
- 到:self.fc = Linear(in_features=980, out_features=10)
# 定义 SimpleNet 网络结构
import paddle
from paddle.nn import Conv2D, MaxPool2D, Linear
import paddle.nn.functional as F
# 多层卷积神经网络实现
class MNIST(paddle.nn.Layer):def __init__(self):super(MNIST, self).__init__()# 定义卷积层,输出特征通道out_channels设置为20,卷积核的大小kernel_size为5,卷积步长stride=1,padding=2self.conv1 = Conv2D(in_channels=1, out_channels=20, kernel_size=5, stride=1, padding=2)# 定义池化层,池化核的大小kernel_size为2,池化步长为2self.max_pool1 = MaxPool2D(kernel_size=2, stride=2)# 定义卷积层,输出特征通道out_channels设置为20,卷积核的大小kernel_size为5,卷积步长stride=1,padding=2self.conv2 = Conv2D(in_channels=20, out_channels=20, kernel_size=5, stride=1, padding=2)# 定义池化层,池化核的大小kernel_size为2,池化步长为2self.max_pool2 = MaxPool2D(kernel_size=2, stride=2)# 定义一层全连接层,输出维度是10self.fc = Linear(in_features=980, out_features=10)# 定义网络前向计算过程,卷积后紧接着使用池化层,最后使用全连接层计算最终输出# 卷积层激活函数使用Relu,全连接层激活函数使用softmaxdef forward(self, inputs):x = self.conv1(inputs)x = F.relu(x)x = self.max_pool1(x)x = self.conv2(x)x = F.relu(x)x = self.max_pool2(x)x = paddle.reshape(x, [x.shape[0], 980])x = self.fc(x)return x修改计算损失的函数,从均方误差(常用于回归问题)到交叉熵误差(常用于分类问题),代码如下所示。
- 从:loss = paddle.nn.functional.square_error_cost(predict, label)
- 到:loss = paddle.nn.functional.cross_entropy(predict, label)
def evaluation(model, datasets):model.eval()acc_set = list()for batch_id, data in enumerate(datasets()):images, labels = dataimages = paddle.to_tensor(images)labels = paddle.to_tensor(labels)pred = model(images) # 获取预测值acc = paddle.metric.accuracy(input=pred, label=labels)acc_set.extend(acc.numpy())# #计算多个batch的准确率acc_val_mean = np.array(acc_set).mean()return acc_val_mean#仅修改计算损失的函数,从均方误差(常用于回归问题)到交叉熵误差(常用于分类问题)
def train(model):model.train()#调用加载数据的函数# train_loader = load_data('train')# val_loader = load_data('valid')opt = paddle.optimizer.SGD(learning_rate=0.01, parameters=model.parameters())EPOCH_NUM = 10for epoch_id in range(EPOCH_NUM):for batch_id, data in enumerate(train_loader()):#准备数据images, labels = dataimages = paddle.to_tensor(images)labels = paddle.to_tensor(labels)#前向计算的过程predicts = model(images)#计算损失,使用交叉熵损失函数,取一个批次样本损失的平均值loss = F.cross_entropy(predicts, labels)avg_loss = paddle.mean(loss)#每训练了200批次的数据,打印下当前Loss的情况if batch_id % 200 == 0:print("epoch: {}, batch: {}, loss is: {}".format(epoch_id, batch_id, avg_loss.numpy()))#后向传播,更新参数的过程avg_loss.backward()# 最小化loss,更新参数opt.step()# 清除梯度opt.clear_grad()# acc_train_mean = evaluation(model, train_loader)# acc_val_mean = evaluation(model, val_loader)# print('train_acc: {}, val acc: {}'.format(acc_train_mean, acc_val_mean)) #保存模型参数paddle.save(model.state_dict(), 'mnist.pdparams')#创建模型
model = MNIST()
#启动训练过程
train(model)epoch: 0, batch: 0, loss is: [2.3579125] epoch: 0, batch: 200, loss is: [0.4289544] epoch: 0, batch: 400, loss is: [0.31014374] epoch: 1, batch: 0, loss is: [0.23571382] epoch: 1, batch: 200, loss is: [0.14443767] epoch: 1, batch: 400, loss is: [0.29584044] epoch: 2, batch: 0, loss is: [0.2954171] epoch: 2, batch: 200, loss is: [0.17638636] epoch: 2, batch: 400, loss is: [0.15439035] epoch: 3, batch: 0, loss is: [0.09984577] epoch: 3, batch: 200, loss is: [0.17405878] epoch: 3, batch: 400, loss is: [0.08693444] epoch: 4, batch: 0, loss is: [0.25134712] epoch: 4, batch: 200, loss is: [0.09044845] epoch: 4, batch: 400, loss is: [0.0785885] epoch: 5, batch: 0, loss is: [0.06229271] epoch: 5, batch: 200, loss is: [0.18825674] epoch: 5, batch: 400, loss is: [0.05030152] epoch: 6, batch: 0, loss is: [0.10051466] epoch: 6, batch: 200, loss is: [0.18116194] epoch: 6, batch: 400, loss is: [0.06495788] epoch: 7, batch: 0, loss is: [0.12305102] epoch: 7, batch: 200, loss is: [0.06968503] epoch: 7, batch: 400, loss is: [0.08263568] epoch: 8, batch: 0, loss is: [0.15880015] epoch: 8, batch: 200, loss is: [0.06577106] epoch: 8, batch: 400, loss is: [0.05110953] epoch: 9, batch: 0, loss is: [0.14060621] epoch: 9, batch: 200, loss is: [0.14625353] epoch: 9, batch: 400, loss is: [0.11598101]
虽然上述训练过程的损失明显比使用均方误差算法要小,但因为损失函数量纲的变化,我们无法从比较两个不同的Loss得出谁更加优秀。怎么解决这个问题呢?我们可以回归到问题的本质,谁的分类准确率更高来判断。在后面介绍完计算准确率和作图的内容后,读者可以自行测试采用不同损失函数下,模型准确率的高低。
至此,大家阅读论文中常见的一些分类任务模型图就清晰明了,如全连接神经网络、卷积神经网络,在模型的最后阶段,都是使用Softmax进行处理。
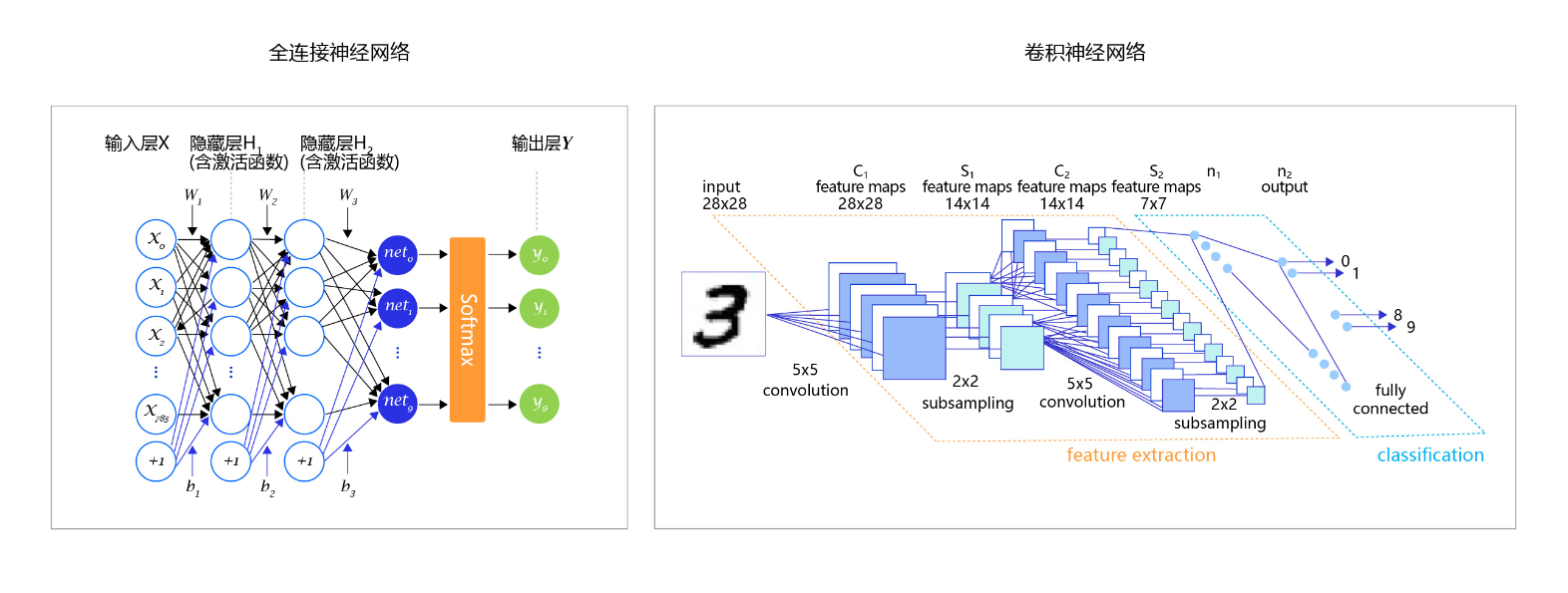
图8:常见的分类任务模型图
由于我们修改了模型的输出格式,因此使用模型做预测时的代码也需要做相应的调整。从模型输出10个标签的概率中选择最大的,将其标签编号输出。
# 读取一张本地的样例图片,转变成模型输入的格式
def load_image(img_path):# 从img_path中读取图像,并转为灰度图im = Image.open(img_path).convert('L')im = im.resize((28, 28), Image.ANTIALIAS)im = np.array(im).reshape(1, 1, 28, 28).astype(np.float32)# 图像归一化im = 1.0 - im / 255.return im# 定义预测过程
model = MNIST()
params_file_path = 'mnist.pdparams'
img_path = 'work/example_0.jpg'
# 加载模型参数
param_dict = paddle.load(params_file_path)
model.load_dict(param_dict)
# 灌入数据
model.eval()
tensor_img = load_image(img_path)
#模型反馈10个分类标签的对应概率
results = model(paddle.to_tensor(tensor_img))
#取概率最大的标签作为预测输出
lab = np.argsort(results.numpy())
print("本次预测的数字是: ", lab[0][-1])本次预测的数字是: 0








![[完美解决]Vue项目运行时出现this[kHandle] = new _Hash(algorithm, xofLen)](https://img-blog.csdnimg.cn/e5923ffacb5544fca808504408ea9cbe.png)