图1

二、插值和外推

        有时，时间序列数据集中存在缺失值。例如，可能存在第 1 年到 3 年的利率，然后是第 5 年到 8 年，然后是第 10 年。纳尔逊-西格尔模型也可用于预测或推断超出可用数据时间段的未来时间段的值。

        已知 X 值表示轴上的值是预先已知的值，例如时间或年份），已知 Y 值表示 y 轴上的值（在本例中为已知利率）。y 轴变量通常是您希望从将来插入缺失值或将值外推到将来的变量。

三、纳尔逊-西格尔-斯文森〔1994〕 模特

        Nelson-Siegel-Svensson（1994）模型用于生成利率和收益率曲线估计的期限结构。需要计量经济学建模技术来校准此模型中多个输入的值。

        Nelson-Siegel-Svensson （1994） 模型通过添加额外的广义参数来修改 Nelson-Siegel （1987） 模型。虚拟任何收益率曲线形状都可以使用这两种模型进行插值，这两种模型在世界各地的银行中广泛使用。

        Nelson-Siegel-Svensson （1994） 模型使用 6 个曲线估计参数运行，而 Nelson-Siegel （1987） 模型使用 4 个曲线估计参数运行。如果建模得当，Nelson-Siegel-Svensson（1994）模型几乎可以适应任何收益率曲线形状。

        校准Nelson-Siegel-Svensson（1994）模型中的输入需要计量经济学建模和误差优化技术。Nelson-Siegel-Svensson（1994）模型用于“填补缺失的现货收益率和利率期限结构的空白”，该模型可用于插值利率时间序列中的缺失数据点（以及其他宏观经济变量，如通货膨胀率和商品价格或市场回报），也可用于推断给定或已知范围之外， 用于预测目的。

四、纳尔逊-西格尔-斯文森收益率曲线拟合法

        纳尔逊-西格尔方法以其简单性而闻名，但它可能无法与在紧张的市场环境中观察到的所有到期日的零收益率相匹配。

图2

1994年，斯文森试图通过在现有的纳尔逊-西格尔公式中添加一个额外的项来创建更灵活的版本，该公式包含两个额外的参数。他漂亮而简单的想法是通过重用他前任方程的最后一个项来创建附加项。

这是最终公式：

图3

其中 β0、β1、β2、β3、λ0 和 λ1 是常数参数，T 是以年为单位的成熟时间。

在我们进入任何python之前，让我们描述一下我们的问题。

五、根本问题

        我们生活在一个叫以色列的国家（以色列在中东的某个地方，它的首都叫耶路撒冷）。在耶路撒冷坐落着以色列的中央银行，称为以色列银行。

        以色列银行提供标准的无风险收益率曲线，是该国风险最低的银行（因此，它提供标准收益率曲线。例如，假设以色列银行只有一定数量的债券。

        让我们看看以色列政府目前有哪些债券未偿还。所以它有：

• 1年期债券，目前的收益率为0.39%。
• 2年期债券，目前的收益率为0.61%。
• 5年期债券，目前的收益率为1.66%。
• 10年期债券，目前的收益率为2.58%。
• 25年期债券，目前的收益率为3.32%。

        好吧，这很好，唯一的问题是，如果我们从这些数字建立收益率曲线，问题是我们之间没有任何数字。我们希望得到一个漂亮的收益率曲线。

        为什么我们要得到一个完整的漂亮曲线？例如，之所以说原因是因为我们有一个客户在以色列与我们联系，为了从这个特定客户那里获得 10，000，000 以色列谢克尔 （ILS） 的利润，我们需要对两件事有一个非常好的估计：

• 以色列银行20年期国债收益率。
• 以色列银行30年期国债收益率。

        不幸的是，当然，正如我们从我们的列表中看到的那样，我们没有这些数字，我们有10年，我们有25年，但我们没有20年，我们没有30年。那么，我们是否要向客户的ILS 10，000，000利润挥手告别？或者我们是否会有一个非常好的受过教育的尝试，试图在特定收益率曲线上创造那些缺失的点点滴滴？

嗯，我们可以。我们可以使用一种叫做纳尔逊-西格尔-斯文森方法的东西来产生真正有根据的猜测，关于中间的那些位应该是什么，以及那些外推的点应该是什么。

六、The Jupyter Notebook

        让我们创建一个新的 jupyter 笔记本。

from scipy.optimize import fmin
import pandas as pd
import numpy as np
import matplotlib.pyplot as pltdd = pd.read_csv('ns.csv')
df = dd.copy()
df.style.format({'Maturity': '{:,.0f}'.format,'Yield': '{:,.2%}'})

图4

        你会注意到我们没有我们想插值的20年，我们没有我们想推断的30年，因为如果我们能推断这些东西，那么我们将计算出这些数字。我们将能够获得10，000，000新谢克尔的利润，这就是我们想要做的。

sf = df.copy()
sf = sf.dropna()
sf1 = sf.copy()
sf1['Y'] = round(sf['Yield']*100,4)
sf = sf.style.format({'Maturity': '{:,.2f}'.format,'Yield': '{:,.4%}'})
import matplotlib.pyplot as plt
import matplotlib.markers as mk
import matplotlib.ticker as mtick
fontsize=15
fig = plt.figure(figsize=(13,7))
plt.title("Nelson-Siegel-Svensson Model - Unfitted Yield Curve",fontsize=fontsize)
ax = plt.axes()
ax.set_facecolor("black")
fig.patch.set_facecolor('white')
X = sf1["Maturity"]
Y = sf1["Y"]
plt.scatter(X, Y, marker="o", c="blue")
plt.xlabel('Period',fontsize=fontsize)
plt.ylabel('Interest',fontsize=fontsize)
ax.yaxis.set_major_formatter(mtick.PercentFormatter())
ax.xaxis.set_ticks(np.arange(0, 30, 5))
ax.yaxis.set_ticks(np.arange(0, 4, 0.5))
ax.legend(loc="lower right", title="Yield")
plt.grid()
plt.show()

图5

所以，你可以看到我们这里有这种粗糙的收益率曲线。我们需要知道20年和30年。让我们看看我们将如何获得这种纳尔逊-西格尔-斯文森方法。

我们需要做的第一件事是输入 3 个校准数字。如果您在互联网上搜索纳尔逊-西格尔-斯文森模型，您会发现您可以输入的这些校准数字。

我建议这些是相当不错的猜测，因此对于 4 个 beta 数字，将 0.01 放入 2 个 lambda 放射性衰变样式数字，我建议 1.0 是一个很好的起始值。现在这些将由一个名为scipy.optimize.fmin的函数进行更改。

β0 = 0.01
β1 = 0.01
β2 = 0.01
β3 = 0.01
λ0 = 1.00
λ1 = 1.00

        我们现在要做的是构建一条曲线，这条曲线不会有任何好处，但稍后会通过称为 fmin 函数的特殊 scipy.optimize 魔法进行更改。我需要在我的数据帧上名为“NSS”的新列中构建另一条曲线，当我在此列中构建另一条曲线时，神奇的技术解决方案将移动这些曲线以使收益率曲线（即我的数据帧上的“收益率”列）符合上述数字。

        让我们把 Nelson-Siegel-Svensson 公式放在这里，我们现在要使用它

df['NSS'] = (β0)+(β1*((1-np.exp(-df['Maturity']/λ0))/(df['Maturity']/λ0)))+(β2*((((1-np.exp(-df['Maturity']/λ0))/(df['Maturity']/λ0)))-(np.exp(-df['Maturity']/λ0))))+(β3*((((1-np.exp(-df['Maturity']/λ1))/(df['Maturity']/λ1)))-(np.exp(-df['Maturity']/λ1))))
df.style.format({'Maturity': '{:,.0f}'.format,'Yield': '{:,.2%}','NSS': '{:,.2%}'})

图6

让我们可视化未拟合的收益率曲线

df1 = df.copy()
df['Y'] = round(df['Yield']*100,4)
df['NSS'] =(β0)+(β1*((1-np.exp(-df['Maturity']/λ0))/(df['Maturity']/λ0)))+(β2*((((1-np.exp(-df['Maturity']/λ0))/(df['Maturity']/λ0)))-(np.exp(-df['Maturity']/λ0))))+(β3*((((1-np.exp(-df['Maturity']/λ1))/(df['Maturity']/λ1)))-(np.exp(-df['Maturity']/λ1))))
df['N'] = round(df['NSS']*100,4)
df2 = df.copy()
df2 = df2.style.format({'Maturity': '{:,.2f}'.format,'Y': '{:,.2%}', 'N': '{:,.2%}'})
import matplotlib.pyplot as plt
import matplotlib.markers as mk
import matplotlib.ticker as mtick
fontsize=15
fig = plt.figure(figsize=(13,7))
plt.title("Nelson-Siegel-Svensson Model - Unfitted Yield Curve",fontsize=fontsize)
ax = plt.axes()
ax.set_facecolor("black")
fig.patch.set_facecolor('white')
X = df["Maturity"]
Y = df["Y"]
x = df["Maturity"]
y = df["N"]
ax.plot(x, y, color="orange", label="NSS")
plt.scatter(x, y, marker="o", c="orange")
plt.scatter(X, Y, marker="o", c="blue")
plt.xlabel('Period',fontsize=fontsize)
plt.ylabel('Interest',fontsize=fontsize)
ax.yaxis.set_major_formatter(mtick.PercentFormatter())
ax.xaxis.set_ticks(np.arange(0, 30, 5))
ax.yaxis.set_ticks(np.arange(0, 4, 0.5))
ax.legend(loc="lower right", title="Yield")
plt.grid()
plt.show()

图7

        我们现在得到的是，我们现在已经走了未拟合的曲线，这就像我们制作西装之前西装的材料一样，我们将对这些校准统计数据进行一些定制，我们将使西装适合蓝点，我们将使用特殊的 fmin 函数来做到这一点。在我们执行此操作之前，我需要在数据帧上名为“残差”的新列中构建另一条曲线。

        我们采用一种称为特殊残差的东西，我们将采用蓝点和未拟合曲线之间的一些误差。我们将采用这些错误，然后对这些错误进行平方以消除任何负号。

df['Residual'] =  (df['Yield'] - df['NSS'])**2
df22 = df[['Maturity','Yield','NSS','Residual']]  
df22.style.format({'Maturity': '{:,.0f}'.format,'Yield': '{:,.2%}','NSS': '{:,.2%}','Residual': '{:,.9f}'})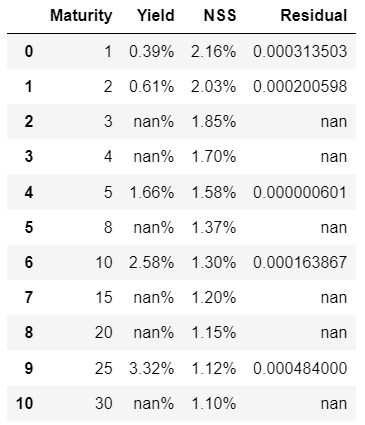

 

图8

        现在我们采用存在于蓝点和蓝点存在的橙色点之间的所有这些误差项，因此我们采用这些项对它们进行平方。然后我要做的是把它们都加起来。

np.sum(df['Residual'])

0.0011625691502601255

        现在这就是魔力的用武之地。我要做的是调用 fmin 函数，我将在上述 6 个值上运行它，求解将上下摇晃这些东西，上下摇晃，上下，上下，这将使“NSS”列上的值上下波动， 上下，上下，我们将尝试最小化“残差”列上的值，使它们共同加起来尽可能低的数字，这样做希望它们会使这条橙色线适合这条虚线蓝线。

        我们希望通过更改上述 6 个数字来最小化“残差”列的总和，使其尽可能小。在这里，我们可以接受负数，没有问题，只需设置默认算法，然后调用fmin。

def myval(c):df = dd.copy()df['NSS'] =(c[0])+(c[1]*((1-np.exp(-df['Maturity']/c[4]))/(df['Maturity']/c[4])))+(c[2]*((((1-np.exp(-df['Maturity']/c[4]))/(df['Maturity']/c[4])))-(np.exp(-df['Maturity']/c[4]))))+(c[3]*((((1-np.exp(-df['Maturity']/c[5]))/(df['Maturity']/c[5])))-(np.exp(-df['Maturity']/c[5]))))df['Residual'] =  (df['Yield'] - df['NSS'])**2val = np.sum(df['Residual'])print("[β0, β1, β2, β3, λ0, λ1]=",c,", SUM:", val)return(val)c = fmin(myval, [0.01, 0.01, 0.01, 0.01, 1.00, 1.00])

        所发生的情况是，解算器根据我的原始输入上下抖动了上述 6 个数字，使橙色曲线符合我们之前看到的那些蓝色点。这不是一个奇妙的魔法吗？

        现在，让我们得到 6 位数字的结果

β0 = c[0]
β1 = c[1]
β2 = c[2]
β3 = c[3]
λ0 = c[4]
λ1 = c[5]
print("[β0, β1, β2, β3, λ0, λ1]=", [c[0].round(2), c[1].round(2), c[2].round(2), c[3].round(2), c[4].round(2), c[5].round(2)])

让我们可视化拟合的收益率曲线

df = df1.copy()
df['NSS'] =(β0)+(β1*((1-np.exp(-df['Maturity']/λ0))/(df['Maturity']/λ0)))+(β2*((((1-np.exp(-df['Maturity']/λ0))/(df['Maturity']/λ0)))-(np.exp(-df['Maturity']/λ0))))+(β3*((((1-np.exp(-df['Maturity']/λ1))/(df['Maturity']/λ1)))-(np.exp(-df['Maturity']/λ1))))
sf4 = df.copy()
sf5 = sf4.copy()
sf5['Y'] = round(sf4['Yield']*100,4)
sf5['N'] = round(sf4['NSS']*100,4)
sf4 = sf4.style.format({'Maturity': '{:,.2f}'.format,'Yield': '{:,.2%}', 'NS': '{:,.2%}'})
M0 = 0.00
M1 = 3.50
import matplotlib.pyplot as plt
import matplotlib.markers as mk
import matplotlib.ticker as mtick
fontsize=15
fig = plt.figure(figsize=(13,7))
plt.title("Nelson-Siegel-Svensson Model - Fitted Yield Curve",fontsize=fontsize)
ax = plt.axes()
ax.set_facecolor("black")
fig.patch.set_facecolor('white')
X = sf5["Maturity"]
Y = sf5["Y"]
x = sf5["Maturity"]
y = sf5["N"]
ax.plot(x, y, color="orange", label="NSS")
plt.scatter(x, y, marker="o", c="orange")
plt.scatter(X, Y, marker="o", c="blue")
plt.xlabel('Period',fontsize=fontsize)
plt.ylabel('Interest',fontsize=fontsize)
ax.yaxis.set_major_formatter(mtick.PercentFormatter())
ax.xaxis.set_ticks(np.arange(0, 30, 5))
ax.yaxis.set_ticks(np.arange(0, 4, 0.5))
ax.legend(loc="lower right", title="Yield")
plt.grid()
plt.show()

图12

这个纳尔逊-西格尔-斯文森方程非常出色，它可能是这类方程中最好的一个，它比创建这些非线性线和这些曲线的多项式方程更好，大多数中央银行和软件绘制这些类型的线正在使用这种纳尔逊-西格尔-斯文森方法来创建这些线。

df.style.format({'Maturity': '{:,.0f}'.format,'Yield': '{:,.2%}','NSS': '{:,.2%}'})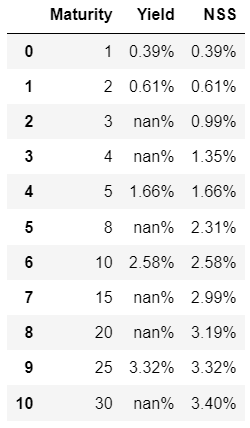

 

        你可以看到这在创建完整的收益率曲线方面做得有多好，现在我可以看到20年期可能收益率为3.2%，我推断出30年期可能收益率为3.4%。所以，我认为这很好，这意味着我们现在可以获得10，000，000新谢克尔的利润。

        这就是您实现纳尔逊-西格尔-斯文森方法的方式，以便从有限的信息中创建收益率曲线。

七、后记

        希望这篇文章能让您很好地了解如何使用 Nelson-Siegel-Svensson 方法生成收益率曲线。如您所见，它非常简单，简单且快速。

        现在是时候走出去，开始对数据进行插值和推断了。试试这个算法，让我知道它是怎么回事。我很高兴收到有关上述任何内容的反馈或问题。罗伊·波兰尼策