0 引言

集成学习（ensemble learning）是时下非常流行的机器学习算法，它本身不是一个单独的机器学习算法，而是通过在数据上构建多个横型，集成所有模型的建模结果，基本上所有的机器学习领域都可以看到集成学习的身影，在现实中集成学习也有相当大的作用，它可以用来做市场营销模拟的建模，统计客户来源，保留和流失，也可用来预测疾病的风险和病患者的易感性。在现在的各种算法竞赛中，随机森林(入门级别容易上手)，梯度提升树（GBDT）， Xgboost等集成算法的身影也随处可见，可见其效果之好，应用之广。（一些工业级的算法，比如GBDT、XGBOOST、LGBM都是以决策树为积木搭建出来的）

多个模型集成后的模型叫做集成评估器，集成评估器中的每一个模型叫做基评估器，通常来说有三类集成算法：Bagging、Boosting、Stacking。随机森林是Bagging的代表模型, 他所有的基评估器都是决策树。Bagging法中每一个基评估器是平行的，最后的结果采用平均值或者少数服从多数的原则。集成算法会考虑多个评估器的建模结果，汇总之后得到一个综合结果，以此来获取比单个模型更好的回归或分类表现。

1 随机森林（RF）简介

一棵棵决策树构成了整个随机森林，具体构建树的数量，在scikit-learn中，用“n_estimators”这个参数来控制。在训练某棵树的时候，也不是将样本的所有特征都用来训练，而是会随机选择一部分特征用来训练，目的就是让不同的树重点关注不同的特征。在scikit-learn中，用“max_features”这个参数来控制训练每棵树选取的样本数）。

只要了解决策树的算法，那么随机森林是相当容易理解的。随机森林的算法可以用如下几个步骤概括：

用有抽样放回的方法（bootstrap）从样本集中选取n个样本作为一个训练集
用抽样得到的样本集生成一棵决策树。在生成的每一个结点：
2.1. 随机不重复地选择d个特征。
2.2 利用这d个特征分别对样本集进行划分，找到最佳的划分特征（可用基尼系数、增益率或者信息增益判别）。
重复步骤1到步骤2共k次，k即为随机森林中决策树的个数。
用训练得到的随机森林对测试样本进行预测，并用票选法决定预测的结果。
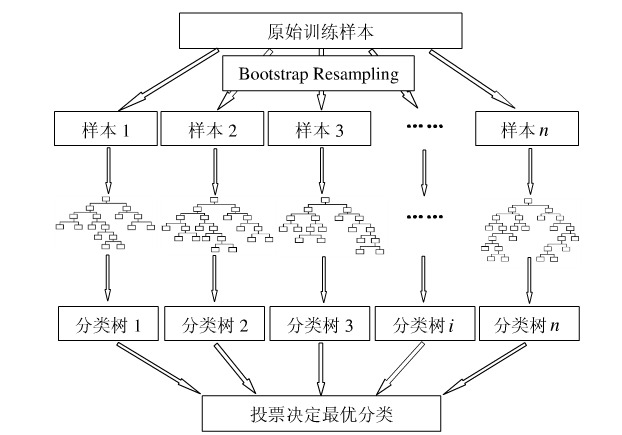
下图比较直观地展示了随机森林算法（图片出自文献2）：

包外估计（Out-of-Bag Estimate）

在随机森林构造过程中进行有放回抽样，一部分样本选不到，这部分样本占整体样本的比重为：
$\lim_{N -> \infty}(1-\frac{1}{N})^N=\frac{1}{e}$

故有36.8%的数据作为包外数据，可用作验证集。包外估计是对集成分类器泛化误差的无偏估计。

3 特征重要性评估

现实情况下，一个数据集中往往有成百上前个特征，如何在其中选择比结果影响最大的那几个特征，以此来缩减建立模型时的特征数是我们比较关心的问题。这样的方法其实很多，比如主成分分析，lasso等等。不过，这里我们要介绍的是用随机森林来对进行特征筛选。

用随机森林进行特征重要性评估的思想其实很简单，说白了就是看看每个特征在随机森林中的每颗树上做了多大的贡献，然后取个平均值，最后比一比特征之间的贡献大小。

3 随机森林优缺点

3.1 优点

随机森林机制简单，泛化能力强，可以并行实现（sklearn中n_jobs控制），因为训练时树与树之间是相互独立的；
随机森林能处理很高维度的数据（也就是很多特征的数据），并且不用做特征选择。
在训练完之后，随机森林能给出哪些特征比较重要。
相比单一决策树，能学习到特征之间的相互影响，且不容易过拟合；
能直接特征很多的高维数据，因为在训练过程中依旧会从这些特征中随机选取部分特征用来训练；
相比SVM，不是很怕特征缺失，因为待选特征也是随机选取；
训练完成后可以给出特征重要性。当然，这个优点主要来源于决策树。因为决策树在训练过程中会计算熵或者是基尼系数，越往树的根部，特征越重要。

3.2 缺点

随机森林在解决回归问题时，并没有像它在分类中表现的那么好，这是因为它并不能给出一个连续的输出。当进行回归时，随机森林不能够做出超越训练集数据范围的预测，这可能导致在某些特定噪声的数据进行建模时出现过度拟合。（PS:随机森林已经被证明在某些噪音较大的分类或者回归问题上回过拟合）。
对于许多统计建模者来说，随机森林给人的感觉就像一个黑盒子，你无法控制模型内部的运行。只能在不同的参数和随机种子之间进行尝试。
可能有很多相似的决策树，掩盖了真实的结果。
对于小数据或者低维数据（特征较少的数据），可能不能产生很好的分类。（处理高维数据，处理特征遗失数据，处理不平衡数据是随机森林的长处）。
执行数据虽然比boosting等快（随机森林属于bagging），但比单只决策树慢多了。

机器学习超详细实践攻略(10)：随机森林算法详解及小白都能看懂的调参指南

利用随机森林对特征重要性进行评估

4 Sklearn中随机森林应用

sklearn.ensemble.RandomForestClassifier(n_estimators=10,criterion='gini',max_depth=None,min_samples_split=2,min_samples_leaf=1,min_weight_fraction_leaf=0.0,max_features="auto",max_leaf_nodes=None,min_impurity_decrease=0.0,min_impurity_split=None,bootstrap=True,oob_score=False,n_jobs=1,random_state=None,verbose=0,warm_start=False,class_weight=None
)

参数

n_estimators:对原始数据集进行有放回抽样生成的子数据集个数，即决策树的个数。若n_estimators太小容易欠拟合，太大不能显著的提升模型，所以n_estimators选择适中的数值，版本0.20的默认值是10,版本0.22的默认值是100。
criterion：分裂节点所用的标准，可选“gini”, “entropy”，默认“gini”。
max_depth：限制树的最大深度，超过深度的树枝将被全部剪掉。如果为None，则将节点展开，直到所有叶子都是纯净的(只有一个类)，或者直到所有叶子都包含少于min_samples_split个样本。默认是None。
min_samples_split：拆分内部节点所需的最少样本数：如果为int，则将min_samples_split视为最小值。如果为float，则min_samples_split是一个分数，而ceil（min_samples_split * n_samples）是每个拆分的最小样本数。默认是2。
min_samples_leaf：在叶节点处需要的最小样本数。仅在任何深度的分割点在左分支和右分支中的每个分支上至少留下min_samples_leaf个训练样本时，才考虑。这可能具有平滑模型的效果，尤其是在回归中。如果为int，则将min_samples_leaf视为最小值。如果为float，则min_samples_leaf是分数，而ceil（min_samples_leaf * n_samples）是每个节点的最小样本数。默认是1。
min_weight_fraction_leaf：在所有叶节点处（所有输入样本）的权重总和中的最小加权分数。如果未提供sample_weight，则样本的权重相等。
max_features：寻找最佳分割时要考虑的特征数量：如果为int，则在每个拆分中考虑max_features个特征。如果为float，则max_features是一个分数，并在每次拆分时考虑int（max_features * n_features）个特征。如果为“auto”，则max_features = sqrt（n_features）。如果为“ sqrt”，则max_features = sqrt（n_features）。如果为“ log2”，则max_features = log2（n_features）。如果为None，则max_features = n_features。注意：在找到至少一个有效的节点样本分区之前，分割的搜索不会停止，即使它需要有效检查多个max_features功能也是如此。
max_leaf_nodes：最大叶子节点数，整数，默认为None
min_impurity_decrease：如果分裂指标的减少量大于该值，则进行分裂。
min_impurity_split：决策树生长的最小纯净度。默认是0。自版本0.19起不推荐使用：不推荐使用min_impurity_split，而建议使用0.19中的min_impurity_decrease。min_impurity_split的默认值在0.23中已从1e-7更改为0，并将在0.25中删除。
bootstrap：是否进行bootstrap操作，bool。默认True。如果bootstrap==True，将每次有放回地随机选取样本，只有在extra-trees中，bootstrap=False
oob_score：是否使用袋外样本来估计泛化精度。默认False。
n_jobs：并行计算数。默认是None。等于-1的时候，表示cpu里的所有core进行工作。
random_state：控制bootstrap的随机性以及选择样本的随机性。
verbose：在拟合和预测时控制详细程度。默认是0。
class_weight：每个类的权重，可以用字典的形式传入{class_label: weight}。如果选择了“balanced”，则输入的权重为n_samples / (n_classes * np.bincount(y))。
ccp_alpha：将选择成本复杂度最大且小于ccp_alpha的子树。默认情况下，不执行修剪。
max_samples：如果bootstrap为True，则从X抽取以训练每个基本分类器的样本数。如果为None（默认），则抽取X.shape [0]样本。如果为int，则抽取max_samples样本。如果为float，则抽取max_samples * X.shape [0]个样本。因此，max_samples应该在（0，1）中。是0.22版中的新功能。