目录
1. 题目解析
2. 算法原理
3. 代码编写
写在最后:
1. 题目解析
题目链接:11. 盛最多水的容器 - 力扣(Leetcode)

这道题目也不难理解,
两边的柱子的盛水量是根据短的那边的柱子决定的,
而盛水量就是短的柱子的高度 * 宽度即可。
2. 算法原理
这道题可以用暴力枚举,两层for循环,肯定是可以找到最大的盛水量,
但是作为一道中等题,用暴力会超时,所以我们得想一个更好的解法。
我们来观察一下规律:

以这个图为例;
如果我们让比较高的左边往右遍历,会有两种情况:
1. 如果右边的柱子更高,而宽度变小,盛水量减少,
2. 如果右边的柱子更矮,宽度又变小,盛水量减少。
很明显不太行,
那如果我们让比较矮的右边往左遍历,也会有两种情况:
1. 如果左边的柱子更高,宽度变小,盛水量可能变小,可能不变,可能变大,
2. 如果左边的柱子更矮,宽度变小,盛水量减少。
从上面两种情况来看,我们可以通过不断让矮的一边的柱子往中间遍历,
记录每次出现的最大值,当遍历完之后,我们就能得到最大值了,
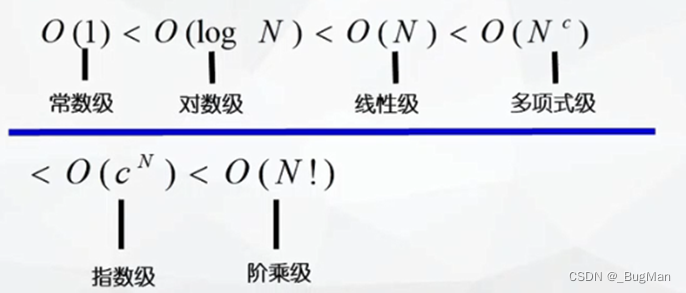
而我们只遍历了一遍,所以时间复杂度就优化到了O(N),
具体做法就是使用双指针来维护两边。
3. 代码编写
class Solution {
public:int maxArea(vector<int>& height) {int left = 0, right = height.size() - 1, maxVal = 0;while(left < right) {maxVal = max(maxVal, min(height[left], height[right]) * (right - left));if(height[left] < height[right]) left++;else right--;}return maxVal;}
};写在最后:
以上就是本篇文章的内容了,感谢你的阅读。
如果感到有所收获的话可以给博主点一个赞哦。
如果文章内容有遗漏或者错误的地方欢迎私信博主或者在评论区指出~