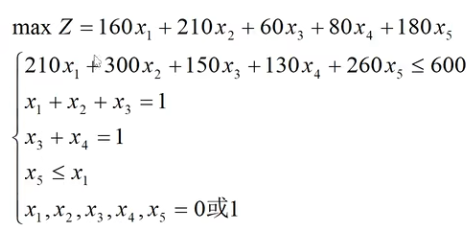数学建模（四）整数规划—匈牙利算法

一、0-1型整数规划问题

1.1 案例

1.2 指派问题的标准形式

2.2 非标准形式的指派问题

二、指派问题的匈牙利解法

2.1 匈牙利解法的一般步骤

2.2 匈牙利解法的实例

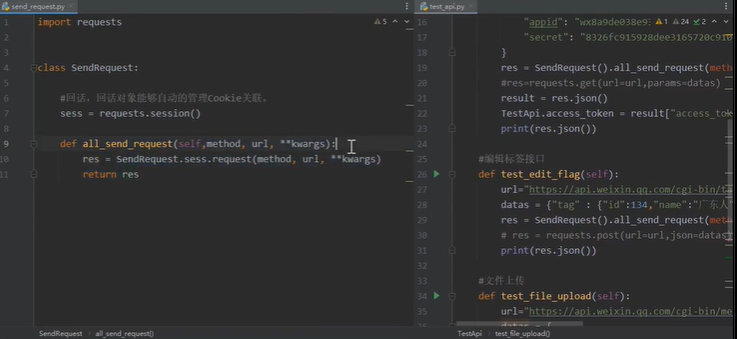
2.3 代码实现

一、0-1型整数规划问题

1.1 案例

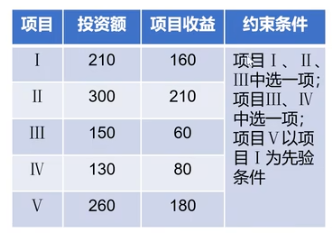
投资问题：

有600万元投资5个项目，收益如表，求利润最大的方案?

设置决策变量：

模型：

指派问题：

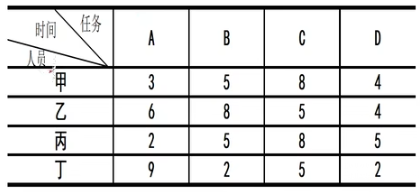
甲乙丙丁四个人，ABCD四项工作，要求每人只能做一项工作，每项工作只由一人完成，问如何指派总时间最短?

设置决策变量：

模型：

约束条件：

1.2 指派问题的标准形式

标准的指派问题：

有n个人和n项工作，已知第i个人做第j项工作的代价为cj(i,j=1,…..,n),要求每项工作只能交与其中一人完成，每个人只能完成其中一项工作，问如何分配可使总代价最少?

指派问题标准求解形式：

（1）指派问题的系数矩阵

（2）决策变量的设置

（3）指派问题的解矩阵

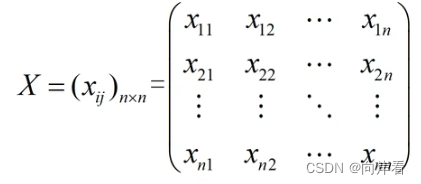
指派问题的可行解中，每行每列有且仅有一个1。

（4）标准模型

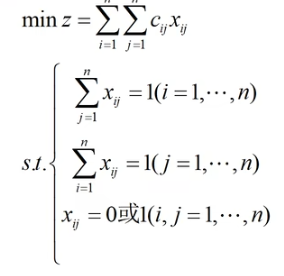
2.2 非标准形式的指派问题

（1）最大化指派问题

例如：求利润，只需找出最大元素，令最大元素减去所有元素，构建一个新的系数矩阵即可。

$C=(c_{ij})_{n \times n}$ 中最大元素为m，令 $B=(b_{ij})_{n \times n}=(m-c_{ij})_{n \times n}$ 。

（2）人数和工作数不等

人少工作多：添加虚拟的 “人”，代价都为0。

人多工作少：添加虚拟的工作，代价都为0。

（3）一个人可做多件工作
该人可化为几个相同的 “人”。

（4）某工作一定不能由某人做
该人做该工作的相应代价取足够大M。例如，将某人做某工作代价设为负值。

二、指派问题的匈牙利解法

匈牙利法是一种求解指派问题的简便解法，它利用了矩阵中0元素的定理。若从系数矩阵的一行(列)各元素中分别减去该行(列)的最小元素，得到新矩阵。以新矩阵为系数矩阵求得的最优解和用原矩阵求得的最优解相同。

2.1 匈牙利解法的一般步骤

第一步：变换指派问题的系数(也称效率)矩阵( $c_{ij}$ )为( $b_{ij}$ )，使在( $b_{ij}$ )的各行各列中都出现0元素，即

(1) 从矩阵( $c_{ij}$ )的每行元素都减去该行的最小元素。
(2) 再从所得新系数矩阵的每列元素中减去该列的最小元素。

第二步：进行试指派，以寻求最优解。

在( $b_{ij}$ )中找尽可能多的独立0元素（即行和列中只有这一个0元素），若能找出n个独立0元素，就以这n个独立0元素对应解矩阵( $x_{ij}$ )中的元素为1，其余为0，这就得到最优解。找独立0元素，常用的步骤为：

(1) 从只有一个0元素的行开始，给这个0元素加圈，记作 $\circledcirc$ ，然后划去 $\circledcirc$ 所在列的其它0元素，记作。这表示这列所代表的任务已指派完，不必再考虑别人了。
(2) 给只有一个0元素的列中的0元素加圈，记作 $\circledcirc$ ，然后划去 $\circledcirc$ 所在行的0元素，记作。
(3) 反复进行(1)，(2)两步，直到尽可能多的0元素都被圈出和划掉为止。
(4) 若仍有没有划圈的0元素，且同行(列)的0元素至少有两个，则从剩有0元素最少的行(列)开始，比较这行各0元素所在列中0元素的数目，选择0元素少的那列的这个0元素加圈。然后划掉同行同列的其它0元素。可反复进行，直到所有0元素都已圈出和划掉为止。
(5) 若 $\circledcirc$ 元素的数目m等于矩阵的阶数n，那么这指派问题的最优解已得到。若m<n,则转入下一步。

第三步：作最少的直线覆盖所有0元素。

(1) 对没有 $\circledcirc$ 的行打√号;
(2) 对已打√号的行中所有含元素的列打√号。
(3) 再对打有√号的列中含 $\circledcirc$ 元素的行打√号。
(4) 重复(2)，(3)直到得不出新的打√号的行、列为止。
(5) 对没有打√号的行画横线，有打√号的列画纵线，这就得到覆盖所有0元素的最少直线数 $l$ 。 $l$ 应等于m，转第四步。若不相等，说明试指派过程有误，回到第二步(4)。

第四步：变换矩阵( $b_{ij}$ )以增加0元素。

在没有被直线覆盖的所有元素中找出最小元素，然后打√各行都减去这最小元素。打√各列都加上这最小元素（以保证系数矩阵中不出现负元素）。新系数矩阵的最优解和原问题仍相同。转回第二步，直到找出最优解。

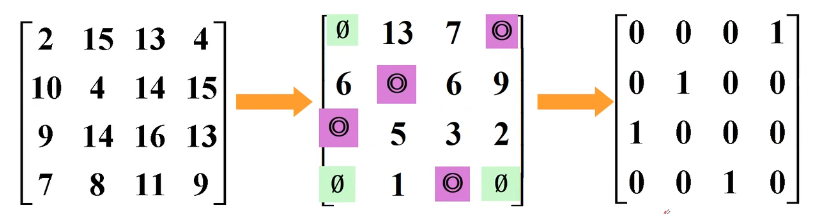
2.2 匈牙利解法的实例

甲乙丙丁四人要完成四项工作A、B、C、D，每人只能完成一项工作，要求完成总时间最短。

匈牙利解法：

第一步：减去最小值。

第二步：加圈和划掉，比较圈数是否等于矩阵的阶数。

等于，则输出最优值，否则，转到第三步重整矩阵。

2.3 代码实现

c=[3 8 2 10 3;8 7 2 9 7;6 4 2 7 5; 8 4 2 3 5;9 10 6 9 10];%系数矩阵c=c(:);    %把矩阵c转化为向量 a=zeros(10,25);for i=1:5   % 实现循环运算
a(i,(i-1)*5+1:5*i)=1; 
a(5+i,i:5:25)=1;
end         % 此循环把指派问题转换为线性规划问题b=ones(10,1); [x,y]=linprog(c,[],[],a,b,zeros(25,1),ones(25,1));X=reshape(x,5,5)opt=y

输出：