---

马尔科夫决策过程

• markov chain：$\mathcal{S}$

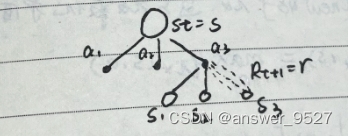
• MRP：$\mathcal{S}，\mathcal{R}$

• MDP：$\mathcal{S}，\mathcal{A}(s)，\mathcal{R}，\mathcal{P}$， P : p = P r { S t + 1 = s ′ , R t + 1 = r ∣ S t = s , A t = a } \mathcal{P}:p=Pr\{S_{t+1}=s',R_{t+1}=r|S_t = s,At = a\} P:p=Pr{St+1​=s′,Rt+1​=r∣St​=s,At=a}

• 状态转移函数：$p(s^{\prime }|s,a)={\sum }_{r\in \mathcal{R}}p(s^{\prime },r|s,a)$
  

• $\pi$（policy）:
  { a = π ( s ) 确定性策略 π ( a ∣ s ) = P r { A t = a ∣ S t = s } 随机性策略 \begin{cases} {a = \pi(s)}& \text{确定性策略}\\ {\pi(a|s )= Pr\{A_t = a|S_t = s}\}& \text{随机性策略} \end{cases} {a=π(s)π(a∣s)=Pr{At​=a∣St​=s}​确定性策略随机性策略​

• $G(Return)$，$\gamma (discount)$:
  $G_t=R_{t+1}+\gamma R_{t+1}...+{\gamma }^{T-1}{R}_T={\sum }_{i=0}^{\infty }{\gamma }_i{R}_{t+i+1}，\gamma \in [0,1]$

• 价值函数：
  { v π ( s ) = E π { G t ∣ S t = s } 状态价值函数 q π ( s , a ) = E π { G t ∣ S t = s , A t = a } 状态动作价值函数 \begin{cases} {v_\pi(s) = E_\pi \{G_t | S_t =s\}}& \text{状态价值函数}\\ {q_\pi(s,a) = E_\pi \{G_t | S_t =s,A_t = a\}}& \text{状态动作价值函数} \end{cases} {vπ​(s)=Eπ​{Gt​∣St​=s}qπ​(s,a)=Eπ​{Gt​∣St​=s,At​=a}​状态价值函数状态动作价值函数​
  $\Rightarrow$ $v_{\pi }(s)={\sum }_{a\in A}\pi (a|s)q_{\pi }(s,a)$
  $\Rightarrow$ q π ( s ) = ∑ s ′ , r { p ( s ′ , r ∣ s , a ) [ r + γ v π ( s ′ ) ] } q_\pi(s) = \sum_{s',r}\{p(s',r|s,a) [r+\gamma v_\pi(s')]\} qπ​(s)=∑s′,r​{p(s′,r∣s,a)[r+γvπ​(s′)]}

• $BellmanExpectationEquation$
  $\{\begin{array}{l}{v}_{\pi }(s)={\sum }_{a\in A}\pi (a|s){\sum }_{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma v_{\pi }(s^{\prime })]\\ q_{\pi }(s,a)={\sum }_{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma {\sum }_{a\in A}\pi (a^{\prime }|s^{\prime })q_{\pi }(s^{\prime },a^{\prime })]\end{array}$

• 最优价值函数
  $\{\begin{array}{ll}{v}_{\ast }(s)=\underset{a}{\max }{v}_{\pi }(s)& \text{最优状态价值函数}\\ q_{\ast }(s,a)=\underset{a}{\max }{q}_{\pi }(s,a)& \text{最优状态动作价值函数}\end{array}$

• $BellmanOptimalityEquation$
  $\{\begin{array}{l}{v}_{\ast }(s)=\underset{a}{\max }{\sum }_{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma v_{\pi }(s^{\prime })]\\ q_{\pi }(s,a)={\sum }_{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma \underset{a}{\max }{q}_{\ast }(s^{\prime },a^{\prime })]\end{array}$

---

动态规划

$策略迭代\{\begin{array}{l}策略评估:已知p(s^{\prime },a|s,a),\forall \pi ,do{q}_{\pi }(s,a)\\ 策略改进:find{\pi }^{\prime },s.t.{\pi }^{\prime }⩾\pi \end{array}$
价值迭代：极端情况下的策略迭代

策略迭代：

1. 解析解：$v_{\pi }(s)=r_{\pi }(s)+\gamma {\sum }_{s^{\prime }}{P}_{\pi }(s,s^{\prime })v_{\pi }(s)=(I-\gamma P_{\pi }{)}^{-1}{\gamma }_{\pi }，O(|s{|}^3)$
2. 数值解：迭代策略评估
   构造数列$v_k，s.t.\underset{k\to \infty }{\lim }{v}_k=v_{\pi }$
   迭代公式：$v_{k+1}={\sum }_a\pi (a|s){\sum }_{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma v_k(s^{\prime })]$
   $v_{\pi }={\sum }_a\pi (a|s){\sum }_{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma v_{\pi }(s^{\prime })]$ (由不动点定理$\Rightarrow v_k\to v_{\pi }$)

策略改进：

• 策略改进定理：给定$\pi ,{\pi }^{\prime },if\forall s\in S,then{v}_{\pi }(s)⩽q_{\pi }(s,{\pi }^{\prime }(s)),so\forall s\in S,v_{\pi }(s)⩽v_{\pi }^{\prime }(s)$
• $GreedyPolicy:\forall s\in S,s.t.{\pi }^{\prime }(s)=arg\underset{a}{\max }{q}_{\pi }(s,a)$
  由策略改进定理可知：$\forall s\in S,v_{\pi }^{\prime }(s)⩾v_{\pi }(s)$
• 问题：迭代中套迭代，${\pi }_1\to v_{\pi 1}\to {\pi }_2\to v_{\pi 2}...{\pi }_{\ast }\to v_{\ast }$
  

解决：截断策略评估(策略评估只进行半步)，${\pi }_1\to v_1(s)$
可简化为：$v_{k+1}=\underset{a}{\max }{\sum }_{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma v_k(s^{\prime })]$
迭代序列：
$v_1(s_1)，v_1(s_2)，...，v_1(s_{|s|})，$
$v_2(s_1)，v_2(s_2)，...，v_2(s_{|s|})，$
$...$
$v_k(s_1)，v_k(s_2)，...，v_k(s_{|s|})，$
当状态空间$S$维度较高时，价值迭代人计算量巨大

• 就地策略迭代：随机选取$\forall s$，对其$v_k(s)$更新，完成策略评估
• 广义策略迭代(GPI)

---

蒙特卡洛方法

用采样的方法解决动态特性未知的问题

用MC做策略评估

$v_{\pi }(s)=E_{\pi }[G_t|S_t=s]\approx \frac{1}{N}{\sum }_{i=1}{G}_t^i$（大数定律）

• 首次访问型MC预测
  初始化：$v(s),Return(s),for\forall s\in S$
  循环(每幕)：
  \qquad 由$\pi$生成一幕序列：$S_0,A_0,R_1,S_1,A_1,R_3,...,S_{T-1},A_{T-1},R_T,S_T$
  \qquad 循环每幕，$t=T-1,T-2,...,0$
  \qquad 若$S_t$未曾出现在$S_{0:t-1}$:
  \qquad \qquad 将$G$加入到$Return(S_t)$
  \qquad \qquad $v_s(t)\leftarrow average(Return(S_t))$
  对$q_{\pi }(s,a)$而言，若要用MC做策略评估。须
  $\{\begin{array}{l}无限多幕\\ 试探性出发假设(保证每一对s,a都有非零的概率被选中作为一幕的起点)\end{array}$

基于试探性出发假设的MC控制(策略迭代)

$\{\begin{array}{l}策略评估：I.无限幕，II.试探性出发假设\\ 策略改进：{\pi }_{k+1}(s)=arg\underset{a}{\max }{q}_{{\pi }_k}(s,a)\end{array}$
${\pi }_0\to q_0\to {\pi }_1\to q_1...$（只选一幕做评估）
$q_{{\pi }_k}(s,{\pi }_{k+1}(s))=q_{{\pi }_k}(s,arg\underset{a}{\max }{q}_{{\pi }_k}(s,a))=\underset{a}{\max }{q}_{\pi }(s,a)⩾{\sum }_a{\pi }_k(a|s)q_{{\pi }_k}(s,a)=v_{{\pi }_k(s,a)}$
由策略改进定理：${\pi }_{k+1}⩾{\pi }_k$

同轨 VS 离轨

• 如何避免试探性出发假设(b为软性策略)
  $\{\begin{array}{l}行动策略b:用样本生成的策略，且必须为软性策略\forall s\in S,a\in A(s),有b(a|s)>0\\ 目标策略\pi :待改进、待评估的策略\end{array}$

$\{\begin{array}{l}同轨策略方法：\pi =b，b为软性策略\\ 离轨策略方法：\pi \ne b（采样困难，用重要性采样）\end{array}$

• 重要性采样：
  $E_p[f(x)]=\int p(x)f(x)dx=\int \frac{p(x)}{q(x)}q(x)f(x)dx=\int [\frac{p(x)}{q(x)}f(x)]q(x)dx=E_q[\frac{p(x)}{q(x)}f(x)]\approx \frac{1}{N}{\sum }_{i=1}^N\frac{p(x)}{q(x)}f(x)$

同轨策略的MC控制

• $\epsilon -$贪心策略(设计软性策略)
  给定$\pi ,q_{\pi }(s,a),{\pi }^{\prime }(a|s)=\{\begin{array}{ll}1-\epsilon +\frac{\epsilon }{|A|},& ifa=a^{\ast }=arg\underset{a}{max{q}_{\pi }(s,a)}\\ \frac{\epsilon }{|A|}，& otherwise\end{array}$
  兼顾大部分情况选最优，小部分情况选平均
  

离轨策略的MC策略评估(用b分布采样)

$\pi ,b$固定且已知，用行动策略$b$做试探性采样，基于行动策略改进目标策略$\pi$；解决同轨策略不能学习到最优策略的问题

$v_{\pi }(s)=E_b[{\rho }_{t:T-1}{G}_t|S_t=s]$
${\rho }_{t:T-1}={\prod }_{k=t}^{T-1}\frac{\pi (A_k|S_k)}{b(A_k|S_k)}$，重要度比列因子，此更新方式为全量更新方式，需维护每一幕完整的$G_t$

离轨策略的MC控制

增量更新:
$\{\begin{array}{l}C=C+W\\ V=V+\frac{W}{C}(G-V)\end{array}$