🚩纸上得来终觉浅, 绝知此事要躬行。
🌟主页:June-Frost
🚀专栏:C语言
🔥该篇将探讨 操作符 和 类型转换 对表达式求解的影响。
目录:
- 隐式类型转换
- 算术转换
- 操作符的属性
- ❤️ 结语
隐式类型转换
C的整型算术运算总是至少以缺省(默认)整型类型的精度来进行的。为了获得这个精度,表达式中的字符和短整型操作数在使用之前被转换为普通整型,这种转换称为整型提升。
整型提升规则:
整形提升是按照变量的数据类型的符号位来提升的。
如果是无符号的整形提升,那么高位补0。
为了更好的理解这样的概念,将举一个例子来解释:
#include<stdio.h>
int main()
{char a = 5;char b = 127;char c = a + b;printf("%d\n", c);return 0;
}
-
char a = 5;
5是整型类型,32个bit,补码是00000000 00000000 00000000 00000101,将5存储到a中,a是有符号char类型,只有8个bit,所以要发生截断,将低位的 00000101 存储到a中。 -
char b = 127
同理,127的补码是 00000000 00000000 00000000 01111111 ,存储b时发生截断,所以将低位的 01111111 存储到b中。 -
char c = a + b;
这里的操作数 a 和 b 是字符类型,所以要发生整型提升。

-
printf("%d\n", c);
%d - 10进制的形式打印有符号的整数 , 而c是字符类型,所以再次发生整型提升。

由于这种转换是隐式的,也无法监控到,那如何证明确实有这样的转换呢?
1.
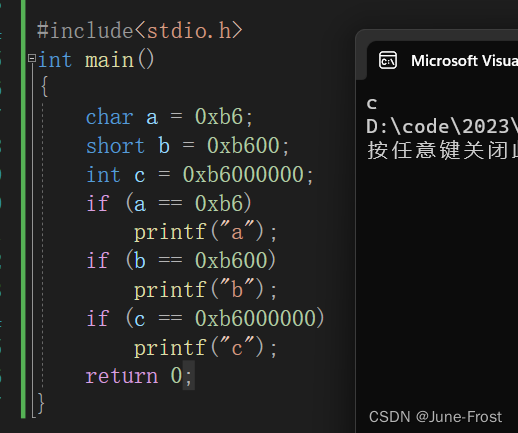
当判断 a == 0xb6 时,a会发生整型提升,由 10110110 变为 11111111 11111111 11111111 10110110 , 本质上 0xb6 是个数值 ,可以看作 00000000 00000000 00000000 10110110 ,这自然是不同的,所以结果是假,b同理,但是c是整型,不需要整型提升,所以表达式 c==0xb6000000 的结果是真 。
2.
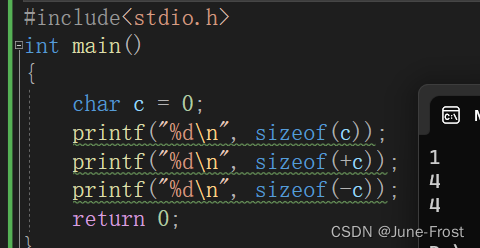
+c 和 -c 参与了表达式运算,发生了整型提升,转化为了普通整型。
通过以上两个例子可以看出,在表达式求解过程中,有着整型提升的参与。
整型提升有两个意义:
1.表达式的整型运算要在CPU的相应运算器件内执行,CPU内整型运算器(ALU)的操作数的字节长度一般就是int的字节长度,同时也是CPU的通用寄存器的长度。因此,即使两个char类型的相加,在CPU执行时实际上也要先转换为CPU内整型操作数的标准长度。
2.通用CPU(general-purpose CPU)是难以直接实现两个8比特字节直接相加运算(虽然机器指令中可能有这种字节相加指令)。所以,表达式中各种长度可能小于int长度的整型值,都必须先转换为int或unsigned int,然后才能送入CPU去执行算。
当表达式中有char 和 short 时,需要整型提升,当表达式中没有这两个类型,只剩下别的类型时,就会有算术转换的参与。
算术转换
如果某个操作符的各个操作数属于不同的类型,那么除非其中一个操作数的转换为另一个操作数的类型,否则操作就无法进行。下面的层次体系称为寻常算术转换。

例如 :int a = 0; float b = 5.5; 如果要执行 a + b , a 会在计算的时候临时转化为float类型,与 b 相加后得到一个 float 类型的结果。
操作符的属性
复杂表达式的求值有3个影响因素:
1.操作符的优先级;
2.操作符的结合性;
3.是否控制求值顺序;
两个相邻的操作符先执行哪个?取决于他们的优先级。如果两者的优先级相同,取决于他们的结合性。
📙操作符属性表(优先级从上至下)
| 操作符 | 描述 | 用法示例 | 结果类型 | 结合性 | 是否控制求值顺序 |
|---|---|---|---|---|---|
| ( | 聚组 | (表达式) | 与表达式同 | N/A | 否 |
| () | 函数调用 | rexp(rexp,…,rexp) | rexp | L-R | 否 |
| [ ] | 下标引用 | rexp[rexp] | lexp | L-R | 否 |
| . | 访问结构成员 | lexp.member_name | lexp | L-R | 否 |
| -> | 访问结构指针成员 | rexp->member_name | lexp | L-R | 否 |
| ++ | 后缀自增 | lexp ++ | rexp | L-R | 否 |
| – | 后缀自减 | lexp – | rexp | L-R | 否 |
| ! | 逻辑反 | ! rexp | rexp | R-L | 否 |
| + | 单目,表示正值 | + rexp | rexp | R-L | 否 |
| - | 单目 ,表示负值 | - rexp | rexp | R-L | 否 |
| ++ | 前缀自增 | ++ lexp | rexp | R-L | 否 |
| – | 前缀自减 | – lexp | rexp | R-L | 否 |
| * | 间接访问 | * rexp | lexp | R-L | 否 |
| & | 取地址 | & lexp | rexp | R-L | 否 |
| sizeof | 取其长度 , 以字节表示 | sizeof rexp sizeof(类型) | rexp | R-L | 否 |
| (类型) | 类型转换 | (类型) rexp | rexp | R-L | 否 |
| * | 乘法 | rexp * rexp | rexp | L-R | 否 |
| / | 除法 | rexp / rexp | rexp | L-R | 否 |
| % | 整数取余 | rexp % rexp | rexp | L-R | 否 |
| + | 加法 | rexp + rexp | rexp | L-R | 否 |
| - | 减法 | rexp - rexp | rexp | L-R | 否 |
| << | 左移位 | rexp << rexp | rexp | L-R | 否 |
| >> | 右移位 | rexp >> rexp | rexp | L-R | 否 |
| > | 大于 | rexp > rexp | rexp | L-R | 否 |
| >= | 大于等于 | rexp >= rexp | rexp | rexp | 否 |
| < | 小于 | rexp < rexp | rexp | L-R | 否 |
| <= | 小于等于 | rexp <= rexp | rexp | L-R | 否 |
| == | 等于 | rexp == rexp | rexp | L-R | 否 |
| != | 不等于 | rexp != rexp | rexp | L-R | 否 |
| & | 位与 | rexp & rexp | rexp | L-R | 否 |
| ^ | 位异或 | rexp ^ rexp | rexp | L-R | 否 |
| I | 位或 | rexp | rexp | rexp | L-R |
| && | 逻辑与 | rexp && rexp | rexp | L-R | 是 |
| II | 逻辑或 | rexp | rexp | rexp | |
| ? : | 条件操作符 | rexp? rexp : rexp | rexp | N/A | 是 |
| = | 赋值 | lexp = rexp | rexp | R-L | 否 |
| += | 以…加 | lexp += rexp | rexp | R-L | 否 |
| -= | 以…减 | lexp -= rexp | rexp | R-L | 否 |
| *= | 以…乘 | lexp *= rexp | rexp | R-L | 否 |
| /= | 以…除 | lexp /= rexp | rexp | R-L | 否 |
| %= | 以…取模 | lexp %= rexp | rexp | R-L | 否 |
| <<= | 以…左移 | lexp <<= rexp | rexp | R-L | 否 |
| >>= | 以…右移 | lexp >>= rexp | rexp | R-L | 否 |
| &= | 以…与 | lexp &= rexp | rexp | R-L | 否 |
| ^= | 以…异或 | lexp ^= rexp | rexp | R-L | 否 |
| I= | 以…或 | lexp I= rexp | rexp | R-L | 否 |
| , | 逗号 | rexp , rexp | rexp | L-R | 是 |
❗️但是就算操作符有这些属性,也不一定会使得表达式有着唯一的求解路径,例如:
例1:
a* b + c * d + e * f;
两种求解路径:

例2:
int c = 3;
c + --c;
这样的表达式有两种路径:

操作符的优先级只能决定自减–的运算在+的运算的前面,但是我们并没有办法得知,+操作符的左操作数的获取在右操作数之前还是之后,所以结果是不可预测的,是有歧义的。
⚠警告:
表达式如果不能通过操作符的属性确定唯一的计算路径,那这个表达式就是存在问题的。
❤️ 结语
文章到这里就结束了,如果对你有帮助,你的点赞将会是我的最大动力,如果大家有什么问题或者不同的见解,欢迎大家的留言~





![[SpringBoot3]远程访问@HttpExchange](https://img-blog.csdnimg.cn/2d4ac3b6f60f4908b0f87c78def0f6a0.png)