排序
下面的代码会用到宏定义,因为再C中没有swap交换函数,所以对于swap的宏定义代码如下:
#define swap(a, b) {\__typeof(a) __a = a; a = b; b = __a;\ }
稳定排序:
1.插入排序:
插入排序会将数组,分位两个部分,一般分为前后两部分,而前半部分为已排序区,后半部分为未排序区;插入排序的操作就是把,未排序区中的元素插入到已排序区中的去,并且满足排序区的单调性;如图下面的操作,实现一个单调递增序列:
数组的原本样子,现在使位置0是已排序区,先去从位置1开始去插入;
将12插入到23前面,使位置0,1形成单调递增;
进行插入,对位置2插入,发现不用插入,直接对下一个位置进行插入:
位置4也不用进行插入保持原位置,对位置5进行插入:
最后完成排序;
时间复杂度:
代码实现:
void insert_sort(int *arr, int n) {//arr排序数组,n数组长度for (int i = 1; i < n; i++) {//位置0开始定为已排序区for (int j = i; j >= 1 && arr[j] < arr[j - 1]; j--) {//将位置i进行插入到前面的以排序区swap(arr[j], arr[j - 1]);//交换位置}}return ; }2.冒泡排序:
冒泡排序,为什么会叫冒泡排序,假如实现单调递增序列,那么每一次都会将未排序中的最大的元素放到未排序区中的最后去,把数组立起来数组的最后的位置在上,那么是不是每次未排序的最大元素会像冒泡一样往上升,所以叫冒泡排序;
如图数组最开始状态:
第一次冒泡:
第一次完冒泡后,最大的元素已经放到了数组最后位置,也相当于放到了已排序区中了;然后这样一直循环直到排完序;
时间复杂度:
代码实现:
做了一个小小的优化;
void bubble_sort(int *arr, int n) {int time = 1;//用来标记这次循环是否发生了冒泡交换for (int i = 1; i < n && time; i++) {//如果没有发生交换说明数组已经排好了序time = 0;for (int j = 0; j < n - i; j++) {if (arr[j] >= arr[j + 1]) {swap(arr[j], arr[j + 1]);time++;}}}return ; }3.归并排序:
将一个数组从中间分开,然后通过递归一直将子数组进行分开,直到数组只有两个元素,然后通过回溯的过程中进行排序,然后一直回溯到整个数组并拢,完成排序;
如图,将数组这样二分下去:
然后从下往上进行排序,单调递增:
合并,排序:
合并,在排序:
最终完成排序;
时间复杂度:
代码实现:
这个过程比较容易理解,就是代码实现有那么一点复杂,来看代码:
void merge_sort(int *arr, int l, int r) {//数组的头位置,r数组的末尾在if (r - l <= 1) {//当分到只有2个元素和1个元素时,递归出口if (r - l == 1 && arr[l] > arr[r]) {//两个元素,进行排序swap(arr[l], arr[r]);}return ;}int mid = (l + r) >> 1;//开始分列merge_sort(arr, l, mid);//递归左边数组merge_sort(arr, mid + 1, r);//递归右边数组int *temp = (int *)malloc(sizeof(int) * (r - l + 1));//创建一个空间,来存子数组的元素int p1 = l, p2 = mid + 1, k = 0;//p1数组分裂开的前部分的起始坐标,p2数组分裂开后半部分的起始坐标while (p1 <= mid || p2 <= r) {if (p2 > r || (p1 <= mid && arr[p1] < arr[p2])) temp[k++] = arr[p1++];else temp[k++] = arr[p2++];}memcpy(arr + l, temp, sizeof(int) * (r - l + 1));//将排好序的子数组拷贝给原数组free(temp);return ; }4.基数排序:
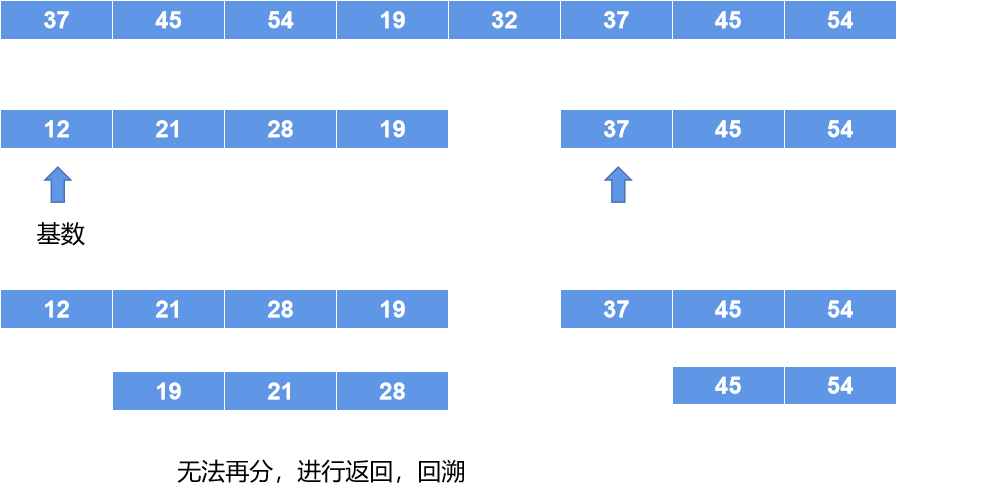
这里假设数组都是两位数,先对数组进行元素的个位进行排序,然后在对数组的十位进行排序,这样就能对数组拍好序;如果位数不相同,取位数最大的数进行位数排序假如最大的位数是3位,那么就进行3次位数排序,如果位数10位那就进行10次位数排序;
如图数组最初:
进行个位排序,上面的表格就是对于个位数的统计,对于排序时会起到作用:

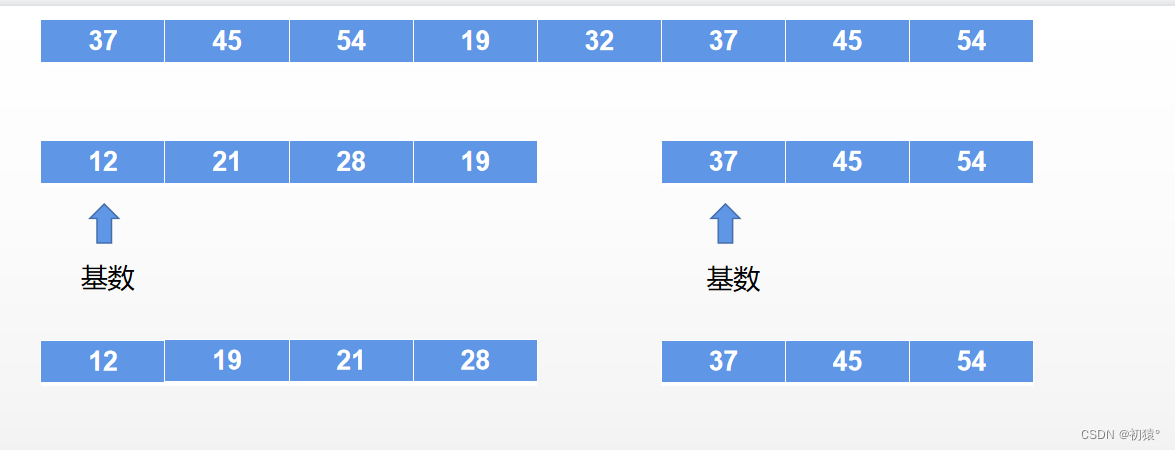
在进行10位排序:
最终完成排序:
时间复杂度:
代码实现:
void number_sort(int *arr, int n, int exp) {int count[10] = {0};for (int i = 0; i < n; i++) {count[arr[i] / exp % 10] += 1;//对每位数的数的个数统计}for (int i = 1; i < 10; i++) {count[i] += count[i - 1];//位数排序,从小到大,现在的操作就是使count变为下标}int *sum = (int *)malloc(sizeof(int) * n);for (int i = n - 1; i >= 0; i--) {//假如个位已近排序后,那么个位大的在后,而根据十位排序也是从高位排到低位,所以需要倒过来存sum[count[arr[i] / exp % 10] - 1] = arr[i];//下标从0开始,所以需要-1;count[arr[i] / exp % 10]--;//对应的位数已经排序一个,所以数量-1;}memcpy(arr, sum, sizeof(int) * n);free(sum);return ; }void radix_sort(int *arr, int n) {int max = INT_MIN;for (int i = 0; i < n; i++) {//获取最大数的数max = max > arr[i] ? max : arr[i];}for (int i = 1; max / i > 0; i *= 10) {//从个位一直到大于最大数的位数number_sort(arr, n, i);}return ; }非稳定排序:
1.选择排序:
将数组分为两个区域一个已排序区和一个未排序区,每次将未排序区中的最值放在已排序区中;
如图将54放放到最后,也就是已排序区中;
这样一直在未排序区中选择,直到排序完成:
时间复杂度:
代码实现:
void select_sort(int *arr, int n) {//这里实现的是将最小的元素放在最前面,现在前面就是已排序区for (int i = 0; i < n - 1; i++) {int ind = i;//ind先记录当前准备排序的位置for (int j = i + 1; j < n; j++) {if (arr[ind] > arr[j]) ind = j;//ind记录未排序区中最小值的值的位置}swap(arr[ind], arr[i]);//将未排序的区的最小值放在准备排序的位置}return ; }2.快速排序:
选择数组头步位置,作为基数,用一个变量记录下来,然后将这个基数作为中间值,将数组分为两个部分,前半部分小于这个基数,后半部分大于基数,然后在对两个部分进行上面的操作,直接这两个部分不能再分;这里不一定是二分开的,有可能这个基数是最大值,那么就没有前半部分;
如图数组初始状态:
将32作为基数,把数组分为两部分分:
然后再对左边部分进行快排,右边部分进行快排
这里只是刚好,不用变化,然后继续上面的操作,直到最后排完序:
完成排序。
时间复杂度:
最坏:
代码实现:
//l最初为0,r最初为n-1 void quick_sort(int *arr, int l, int r) {if (r < l) return ;int x = l, y = r, num = arr[l];while (x < y) {while (x < y && arr[y] >= num) y--;//如果大于基数的部分,该位置数大于基数就不用交换if (x < y) arr[x++] = arr[y];//如果x<y,说明y位置的值是小于基数的,就放到前面去,第一次的时候x的位置就是基数的位置,所以覆盖的是基数的位置while (x < y && arr[x] <= num) x++;//如果小于基数的部分,该位置数小于等于基数就不用交换if (x < y) arr[y--] = arr[x];//x<y,说明x位置的值是小于基数的,现在y位置是之前小于基数的位置,直接覆盖}arr[x] = num;//将基数放到分割位置quick_sort(arr, l, x - 1);//小于基数的部分quick_sort(arr, x + 1, r);//大于基数的部分return ; }3.希尔排序
希尔排序其实就是对于选择排序的一个优化的算法,而最最坏的情况就是降为一个普通的选择排序。
选择一个移动的长度,最开始选择数组长度的1/2,然后一直除2,直到步长等于1,进行一次插入排序;这个步长的作用就是,从一个位置往前移动多少步进行对该位置的值进行比较,如果不满住单调性就进行交换,然后交换如果还能往前目前的步长长度,继续往前比较;
如图,直接上图片理解:
现在的步长选作4,那么就从位置4进行开始排序:
他俩进行比较,然后数组是单调递增,就就需要交换,然后比较位置向后移动:
然后第一次步长结束后,那么步长在除以2:
然后再次进行比较
继续往后
这里发生了交换,而且现在的位置还能往前走步长,所以也需要比较:
比较后,不用发生交换,继续刚刚的位置往后:
这里发生了交换,又需要往前走:
直到不能发生交换,然后现在走到了最后的位置,进行步数除以2,等于1,进行一次选择排序:
这里发生了交换,那就需要再往前走步长那么长进行比较:
最后遍历,没有发生交换,并且步长为除2等于0了,完成排序;
时间复杂度:
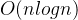
最坏:
代码实现:
void shell_sort(int *arr, int n) {int step;for (step = n / 2; step > 0; step >>= 1) {//步长循环for (int i = step; i < n; i++) {//从步长长度开始往后循环for (int j = i; j >= step && arr[j] < arr[j - step]; j -= step) {//如果不满足单调性,发生交换,并且如果现在的位置长度大于等于步长继续往前移动进行比较swap(arr[j], arr[j - step]);}}}return ; }4.堆排序:
堆,堆排序在前面这个链接的文章里,因为单独将堆排序有那么一点难理解需要结合对堆的理解才容易一些;
算法——排序
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.rhkb.cn/news/114267.html
如若内容造成侵权/违法违规/事实不符,请联系长河编程网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
GPU编程(基于Python和CUDA)(二)——显示GPU信息
系列文章目录
GPU编程(基于Python和CUDA)(一)——零基础安装pycuda GPU编程(基于Python和CUDA)(二)——显示GPU信息 显示GPU信息 系列文章目录前言通过CUDA查看GPU信息使用pycuda查…
CA证书颁发机构服务器
目录 一、CA证书颁发机构是什么? 二、数字证书可以干什么? 三、PKI:即公钥加密体系(public key cryptography) 四、CA在网络中的工作流程及原理(以网站为例) 五、HTTPS 的工作原理 六、CA私有证…
关于CICD流水线的前端项目运行错误,npm项目环境配置时出现报错:Not Found - GET https://registry.npm...
关于CICD流水线的前端项目运行错误,npm项目环境配置时出现报错:Not Found - GET https://registry.npm… 原因应该是某些jar包缓存中没有需要改变镜像将包拉下来 npm config set registry http://registry.npm.taobao.org npm install npm run build
Android 下第一个fragment app 先Java 后Kotlin
看着视频学习的,Fragment:3.Fragment使用方法_哔哩哔哩_bilibili
在android studio 下新建一个工程,类型是 Empty View Activity,本身就有一个Activity。就有文件MainActivity.java 或者kt,还有一个layout 文件&#…
$attrs,$listeners
vue实现组件通信的方式有:
父子通信 父组件向子组件传递通过props定义各个属性来传递,子组件向父组件传递通过$emit触发事件 ref也可以访问组件实例跨级通信 vuex bus provide / inject $attrs / $listeners解释 $attrs / $listeners $attrs 将父组件中…
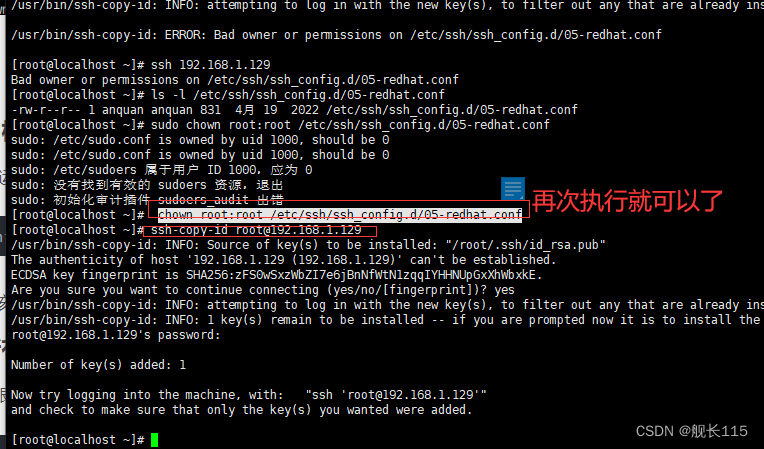
linux免密登录报错 Bad owner or permissions on /etc/ssh/ssh_config.d/05-redhat.conf
问题:权限不对的 解决: 1.检查文件的所有者和权限。
确保文件的所有者是正确的。 运行以下命令来确定文件的所有者和权限: ls -l /etc/ssh/ssh_config.d/05-redhat.conf
通常情况下,SSH配置文件应该属于root用户。如果所有者不是…
前端list列表自定义图标并设置大小
前端list列表自定义图标并设置大小
一、前端list列表基础知识回顾
前端公有两种列表,一种是有序列表(ol),一种是无序列表(ul),它们的子元素都是(li)。
1.1 有序列表&a…
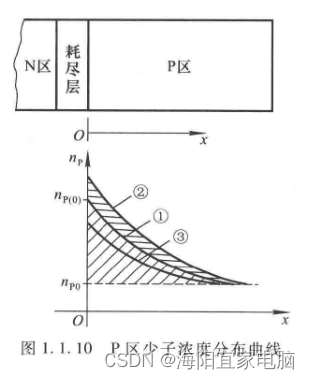
模拟电子技术基础学习笔记三 PN结
采用不周的掺杂工艺,将P型半导体与N型半导体制作在同一块硅片上,在它们的交界面就形成PN结。
扩散运动
物质总是从浓度高的地方向浓度低的地方运动,这种由于浓度差而产生的运动称为扩散运动。
空间电荷区 - 耗尽层 漂移运动
在电场力的作…
(数学) 剑指 Offer 39. 数组中出现次数超过一半的数字 ——【Leetcode每日一题】
❓ 剑指 Offer 39. 数组中出现次数超过一半的数字
难度:简单
数组中有一个数字出现的次数超过数组长度的一半,请找出这个数字。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1: 输入: [1, 2, 3, 2, 2, 2, 5, 4, 2] 输…
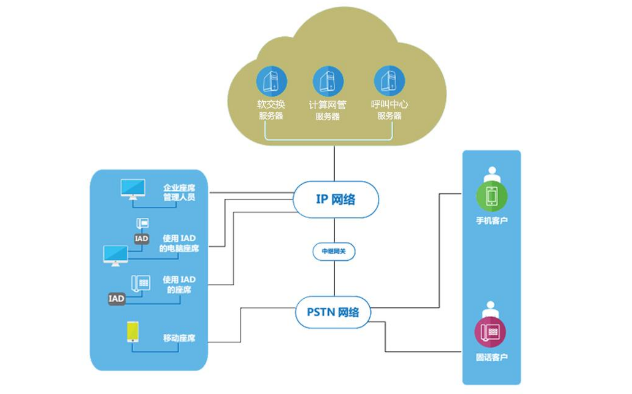
语音专线如何接入呼叫中心系统
想要了解语音专线是否可以接入呼叫中心系统,首先要分别了解什么是语音专线和什么是呼叫中心系统。语音专线接入呼叫中心系统想要实现什么功能,下面小易就来科普一下。 什么是语音专线?语音专线可以理解为联通、电信、移动运营商提供的一种语音…
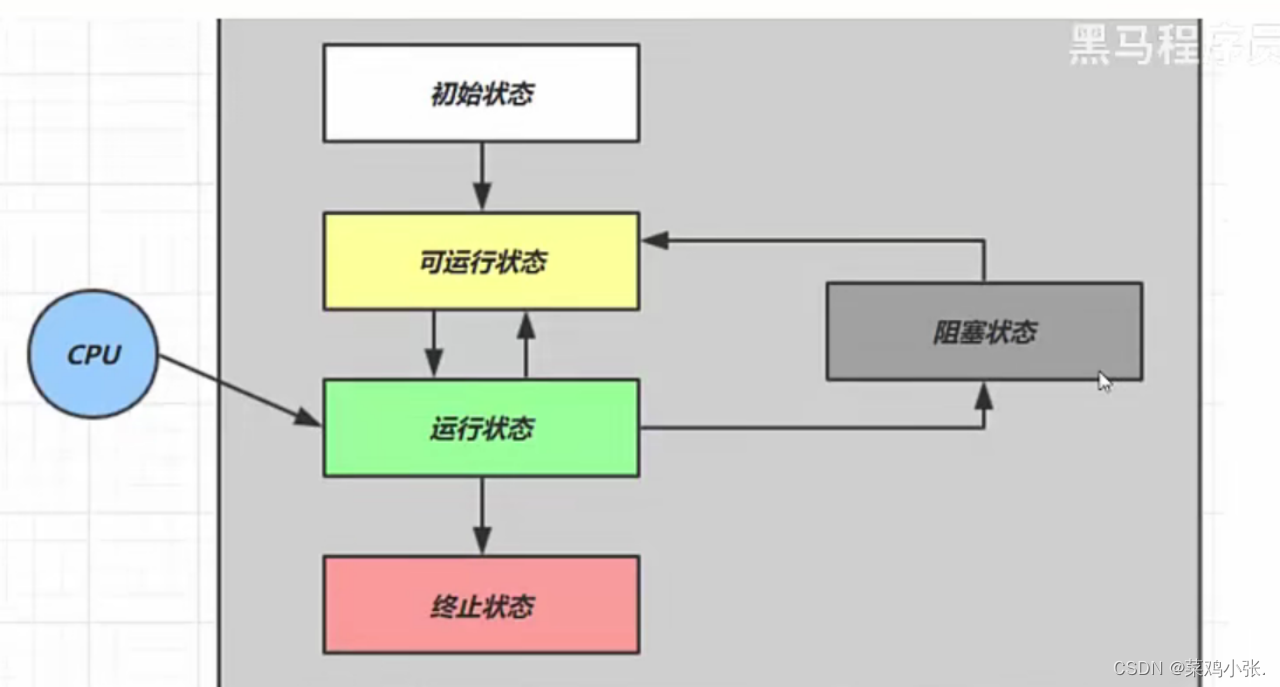
并发编程的故事——Java线程
Java线程 文章目录 Java线程一、线程创建二、线程运行三、线程运行四、主线程和守护线程五、线程的五种状态六、线程的六种状态七、烧水泡茶案例 一、线程创建
创建线程方法一:
Thread重写run方法
Slf4j(topic "c.MyTest1")
public class MyTest1 {publ…
HTML 播放器效果
效果图 实现代码
<!DOCTYPE HTML>
<html><head><title>爱看动漫社区 | 首页 </title><link href"css/bootstrap.css" relstylesheet typetext/css /><!-- jQuery --><script src"js/jquery-1.11.0.min.js"…
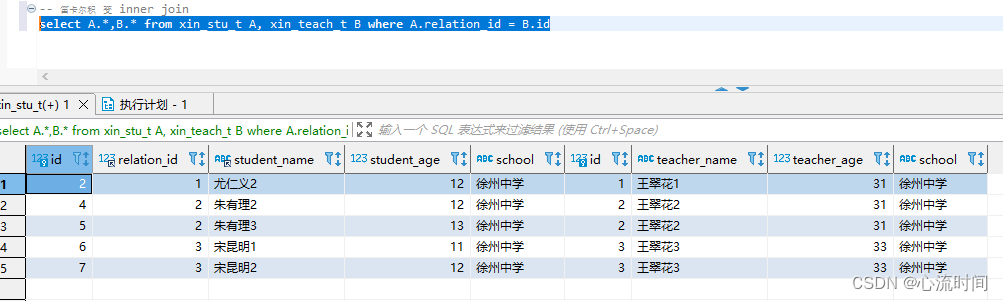
Mysql表关联简单介绍(inner join、left join、right join、full join不支持、笛卡尔积)
文章目录 0. 交集、并集、差集含义说明1. 简单演示上图七种情况0. A、B表数据准备1. left outer join 简称 left join 左表所有数据,右表关联数据,没有的以null填充2. right outer join 简称 right join,右表所有数据,左表关联数据…
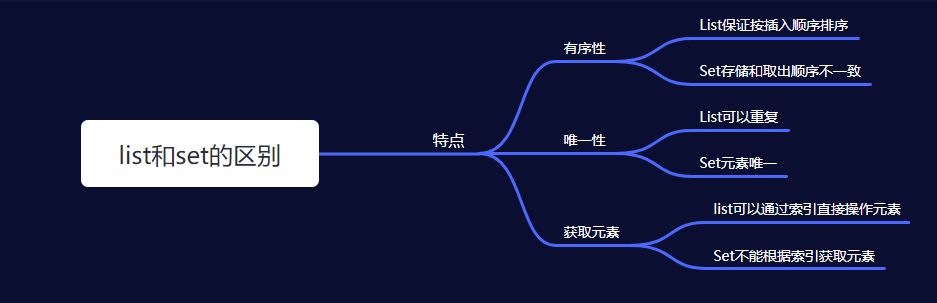
【java中的Set集合】HashSet、LinkedHashSet、TreeSet(最通俗易懂版!!)
目录 一、HashSet集合
1.HashSet集合的特点
2.HashSet常用方法
二、LinkedHashSet集合
LinkedHashSet集合的特点
三、TreeSet集合
1.TreeSet集合的特点
2.TreeSet的基本使用
四、HashSet、LinkedHashSet、TreeSet的使用场景
五、list和set集合的区别 一、HashSet集合 …
【Apollo学习笔记】——规划模块TASK之SPEED_BOUNDS_PRIORI_DECIDER
文章目录 前言SPEED_BOUNDS_PRIORI_DECIDER功能简介SPEED_BOUNDS_PRIORI_DECIDER相关配置SPEED_BOUNDS_PRIORI_DECIDER流程将障碍物映射到ST图中ComputeSTBoundary(PathDecision* path_decision)ComputeSTBoundary(Obstacle* obstacle)GetOverlapBoundaryPointsComputeSTBounda…
Apache SeaTunnel 2.3.3 版本发布,CDC 支持 Schema Evolution!
时隔两个月, Apache SeaTunnel 终于迎来大版本更新。此次发布的 2.3.3 版本在功能和性能上均有较大优化改进,其中大家期待已久的 CDC Schema evolution(DDL 变更同步)、主键 Split 拆分、JDBC Sink 自动建表功能、SeaTunnel Zeta …
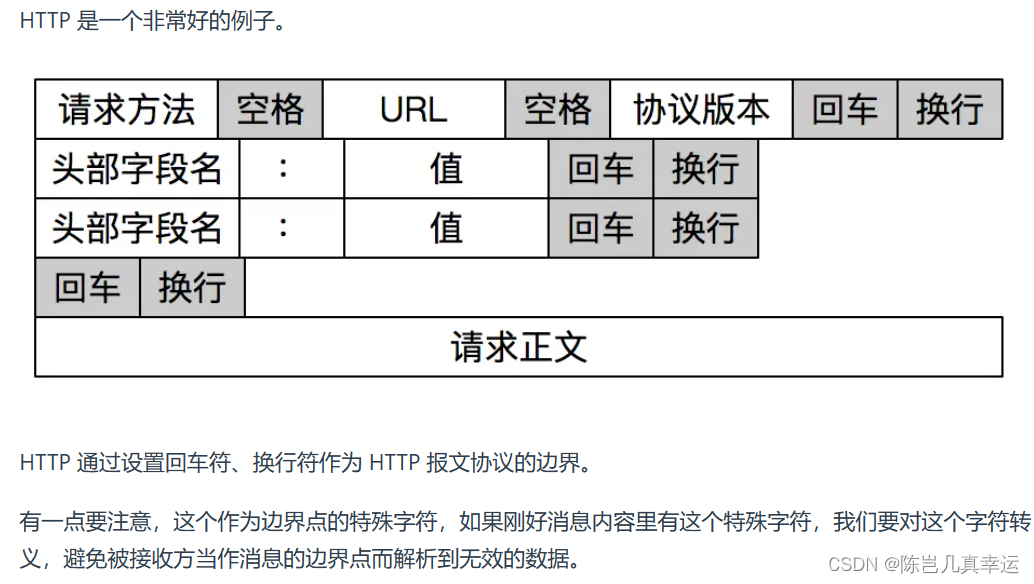
4.6 TCP面向字节流
TCP 是面向字节流的协议,UDP 是面向报文的协议
操作系统对 TCP 和 UDP 协议的发送方的机制不同,也就是问题原因在发送方。
UDP面向报文协议:
操作系统不会对UDP协议传输的消息进行拆分,在组装好UDP头部后就交给网络层处理&…
C++之访问vector<vector<char>>中的vector<char>元素(一百八十七)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 人生格言: 人生…
大模型综述论文笔记6-15
这里写自定义目录标题 KeywordsBackgroud for LLMsTechnical Evolution of GPT-series ModelsResearch of OpenAI on LLMs can be roughly divided into the following stagesEarly ExplorationsCapacity LeapCapacity EnhancementThe Milestones of Language Models Resources…
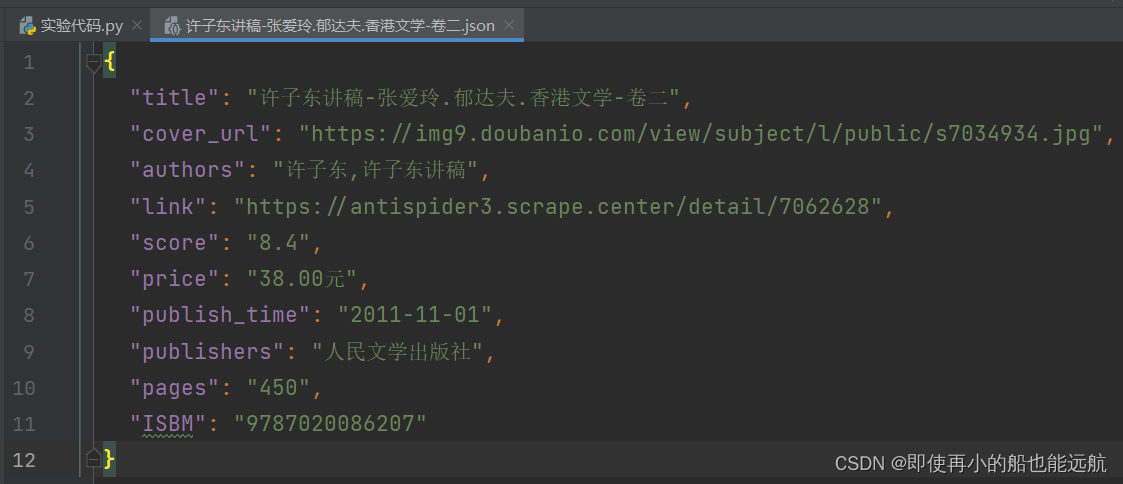
【爬虫】实验项目一:文本反爬网站的分析和爬取
目录
一、实验目的
二、实验预习提示
编辑
三、实验内容 四、实验要求 五、实验过程
1. 基本要求:
2. 改进要求A
3. 改进要求B:
六、资料
1.实验框架代码:
2.OpenSSL:Win32/Win64 OpenSSL Installer for Windows - Shining Light…
推荐文章
- 软考-高级-系统架构设计师教程(清华第2版)【第15章 面向服务架构设计理论与实践(P527~554)-思维导图】
- Linux tac命令
- # Ubuntu 达人九步养成记(1)
- # Vue 入门级教程三
- # 关于Linux下的parted分区工具显示起始点为1049kB的问题解释
- # 消息中间件 RocketMQ 高级功能和源码分析(四)
- #HarmonyOS:Web组件的使用
- #渗透测试#漏洞挖掘#红蓝攻防#SRC漏洞挖掘02之权限漏洞挖掘技巧
- #循循渐进学51单片机#指针基础与1602液晶的初步认识#not.11
- (10)(10.9) 术语表(一)
- (10)svelte 教程:Slots
- (21)多线程实例应用:双色球(6红+1蓝)