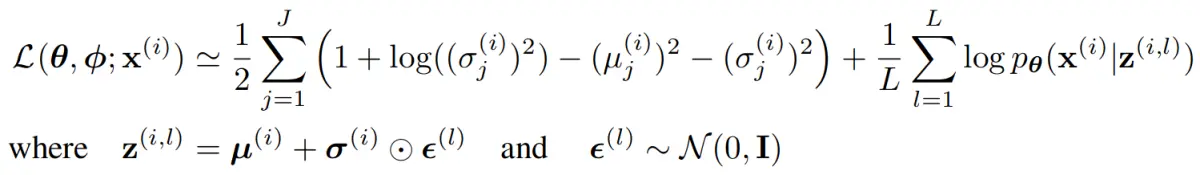英文名称: Auto-Encoding Variational Bayes
中文名称: 自编码变分贝叶斯
论文地址: http://arxiv.org/abs/1312.6114
时间: 2013
作者: Diederik P. Kingma, 阿姆斯特丹大学
引用量: 24840

1 读后感

VAE 变分自编码（Variational Autoencoder）是一种生成模型，它结合了自编码器和概率图模型的思想。它的目标是：解决对复杂性高，且量大的数据难以拟合的问题。具体方法是：使用基于变分推理的原理，以变分下界作为目标函数，用梯度方法求取模型参数。

2 通俗理解

听起来非常抽象，简单地说：变分自编码器是自编码器的改进版。

2.1 自编码器

自编码器通常由编码器和解码器两部分组成，其中编码器将原始数据映射到低维表示，解码器则将低维表示映射回原始数据空间。即：原始数据为x，将其输入编码器降维后，变成数据z，再经过编码器还原成数据 x’。它常用于高维数据的低维表示和从低维表示中生成高维数据。比如：图像去噪，修复图片，生成高分辨率图片等。

2.2 变分自编码器

变分自编码器在中间加了一层逻辑，它假设中间过程的数据 z 每个维度都是正态分布的，可以使用：均值 μ 和 方差 σ 表示。由此，就变成了变分自编码器：训练编码器和解码器网络，可将图片x分布压缩后再拆分成多个高斯分布的叠加，如上图所示。

3 相关概念

3.1 高斯分布

使用高斯分布的原因是：每张训练图片的内容都不一样，训练过程中产生的潜空间z也是离散的，不能确定它的分布。比如数据有满月和半月，但无法产生2/3月亮。而高斯分布是连续的，如果能把中间的表征z用正态分布描述，它就是平滑的，理论上就可以产生介于两图之间的内容图片，它具有一定的潜在空间的连续性和插值性质。

3.2 高斯混合模型 GMM

可以想见，z的分布相当复杂，不是一个简单的高斯分布可以描述的。图中红色为分布曲线。它可分解为一系列不同频率、不同振幅、不同相位的正弦波。也就是说可以用多个正态分布（高斯分布）的叠加去逼近任意一个分布。可以说 VAE 是对 GMM 方法的改进版。

3.3 KL散度

用于衡量两个分布之间的距离。

3.4 最大似然估计

似然与概率类似，但有如下区别：给定一个函数$P(x|\theta )$ ，x是样本点，$\theta$是参数。
（1）当 $\theta$ 为常量， x为变量时，称 P 为关于 x 的概率函数；
（2）当 x 为常量， $\theta$ 为变量时，称 P 为关于 $\theta$ 的似然函数；
求解最大似然是指：求使得样本点 x 能够以最大概率发生的 $\theta$ 的取值。

3.5 变分推断

变分 Variational 是通过引入一个简化的参数化分布来近似复杂的后验分布。这个参数化分布被称为变分分布，它属于一种可计算的分布族。通过调整变分分布的参数，使其尽可能接近真实的后验分布，从而实现近似推断。

3.6 变分下界

变分下界（variational lower bound）通常用于衡量变分分布与真实后验分布之间的差异。
$$ELBO=E[logp(x,z)-logq(z)]$$
其中，ELBO 代表变分下界（Evidence Lower BOund），x代表观测数据，z代表未知变量，p(x, z)表示真实的联合分布，q(z)表示变分分布。

3.7 代入本文中场景

有一张图 x（后验分布），想把它映射成 z，假设 z 是混合高斯分布(先验分布)，各维可能描述颜色，材质……，用函数函数 g() 把 x 分解成高斯分布，它的逆过程是用 f() 根据高斯分布还原原始图 x‘ ，最终恢复的图片 x’=f(g(x))，目标是想让 x’-x 值尽量小，就是说：图 x 转成潜空间 z 再转回原始图 x’，图像最好没变化。
综上所述，无论x是什么，通过变换，产生的x’都与x很像，中间过程的 z 还能用高斯参数表示，求这样的函数f和g的神经网络。

3.8 蒙特卡洛估计

蒙特卡洛估计（Monte Carlo estimation）是一种基于随机抽样的统计估计方法，用于计算复杂问题的数值近似解。其基本思想是通过生成大量的随机样本，利用这些样本的统计特性来估计问题的解。

4 方法

（以下图和公式中的变量含义重新开始定义，不要与上面混淆）

先看一下论文主图，N是数据集，x是真实空间（可观察），z是潜空间（不可观察的连续空间）；实线表示生成模型 pθ(z)pθ(x|z)，虚线表示p的变分近似 qφ(z|x)（也称识别模型），文中使用的方法是用 qφ(z|x) 模拟难以计算的 pθ(z|x)，变分参数 φ 与生成模型参数 θ 一起学习。这里的q可视为编码器，而p视为解码器。

4.1 变分边界

边界似然（Marginal Likelihood）是各观测数据点（每张图片）在给定模型下的概率之和（原图的概率），值越大模型越好，它描述的是图像重建的好不好（重建损失）。
$$log{p}_{\theta }(x^{(1)},\cdot \cdot \cdot ,x^{(N)})=\sum _{i=1}^{N}log{p}_{\theta }(x^{(i)})$$
各数据点的概率：
$$log{p}_{\theta }(x(i))=D_{KL}(q_{\phi }(z|x^{(i)})||p_{\theta }(z|x^{(i))})+L(\theta ,\phi ;x^{(i)})$$
前半部分 DKL 是z的模拟值和真实后验的 KL 散度，KL 散度一定大于0，后半部分 L 是变分下界（建模的目标）：
$$\log p_{\mathbf{\theta }}\left({\mathbf{x}}^{(i)}\right)\ge \mathcal{L}\left(\mathbf{\theta },\mathbf{\varphi };{\mathbf{x}}^{(i)}\right)={\mathbb{E}}_{q_{\mathbf{\varphi }}(\mathbf{z}\mid \mathbf{x})}\left[-\log q_{\mathbf{\varphi }}(\mathbf{z}\mid \mathbf{x})+\log p_{\mathbf{\theta }}(\mathbf{x},\mathbf{z})\right]$$
这里的E是期望，右测是变分下界 ELBO 的公式。
通过移项得到了变分下界的目标函数，公式如下：
$$\mathcal{L}\left(\mathbf{\theta },\mathbf{\varphi };{\mathbf{x}}^{(i)}\right)=-D_{KL}\left(q_{\mathbf{\varphi }}\left(\mathbf{z}\mid {\mathbf{x}}^{(i)}\right)\Vert p_{\mathbf{\theta }}(\mathbf{z})\right)+{\mathbb{E}}_{q_{\mathbf{\varphi }}\left(\mathbf{z}\mid {\mathbf{x}}^{(i)}\right)}\left[\log p_{\mathbf{\theta }}\left({\mathbf{x}}^{(i)}\mid \mathbf{z}\right)\right]$$
目标函数是最大化变分下界（Variational Lower Bound）：第一项 KL散度（Kullback-Leibler Divergence）衡量了潜在变量的分布与先验分布之间的差异（z的差异：越小越好），第二项 重建损失（Reconstruction Loss）衡量了重建样本与原始样本之间相似度（x为原图的概率：越大越好），所以整体 L 越大越好。

z 对应的多个高斯分布的均值和方差都不是固定的值，它们通过神经网络计算得来，神经网络的参数通过训练得到。

4.2 具体实现

这里引入了噪声变量e作为辅助变量，来实现 q 的功能。
$$\tilde{z}=g_{\varphi }(ϵ,x)$$
对某个函数 f(z) 的期望进行蒙特卡洛估计，具体通过采样实现，其minibatch 是从有N个数据点的数据集中，随机抽取M个点：
$$\mathcal{L}(\mathbf{\theta },\mathbf{\varphi };\mathbf{X})\simeq {\tilde{\mathcal{L}}}^M\left(\mathbf{\theta },\mathbf{\varphi };{\mathbf{X}}^M\right)=\frac{N}{M}\sum _{i=1}^M\tilde{\mathcal{L}}\left(\mathbf{\theta },\mathbf{\varphi };{\mathbf{x}}^{(i)}\right)$$
可以将KL散度看成限制参数φ的正则化项。而重建误差部分：先用函数 gφ(.) 将数据点 x 和随机噪声向量映射到该数据点的近似后验样本z，然后计算 log pθ(x(i)|z(i,l))，等于生成模型下数据点 x(i) 的概率密度，从而计算重建误差。

4.3 变分自编码器

在变分自编码器的场景中，先验是中心各向同性的多元高斯分布：
$$\log q_{\mathbf{\varphi }}\left(\mathbf{z}\mid {\mathbf{x}}^{(i)}\right)=\log \mathcal{N}\left(\mathbf{z};{\mathbf{\mu }}^{(i)},{\mathbf{\sigma }}^{2(i)}\mathbf{I}\right)$$
其中均值和标准差是编码 MLP 的输出。由于是高斯分布：
$$z^{(i,l)}=g_{\varphi }(x^{(i)},{ϵ}^{(l)})={\mu }^{(i)}+{\sigma }^{(i)}\odot {ϵ}^{(l)}$$
引入高斯分布的KL散度，最终目标函数是：