前言

这里我先声明一下dp问题的做题方法：

• 1.确定状态表示
• 2.确定状态方程
• 3.处理初始化问题(一般是下标的映射或者初始化保证填表正确)
• 4.确定填表顺序
• 5.根据状态表示确定返回值。

一、斐波那契系列

1.第 N 个泰波那契数

• 链接：点此进入

1. 状态表示：以 i 位置为结尾的第i个斐波那契数。
2. 状态转移方程：dp[i] = dp[i-1] + dp[i-2] + dp[i-3]
3. 初始化——为了防止越界需要判断特殊情况 0, 1 ,2。除此之外需将这三个位置分别初始为 0 ， 1， 1.
4. 填表顺序：从左往右
5. 返回值——dp[n]

class Solution {
public:int tribonacci(int n) {vector<int> dp(n + 1);//初始化if(n == 0)return 0;if(n < 3)  return 1;//保证后续的填表是正确的。dp[1] = dp[2] = 1;//从for(int i = 3; i <= n; i++){dp[i] = dp[i-1] + dp[i-2] + dp[i-3];}return dp[n];}
};

2.三步问题

• 链接：点此进入

1. 状态表示：dp[i]表示以i位置为结尾的所有的爬楼梯的方式。
2. 确定状态转移方程：dp[i] = dp[i-1] + dp[i-2] + dp[i-3]
3. 初始化：防止第0，1，2位置越界需要进行判断，并保证后续的填表是正确的，需要在前三个位置分别填上1，1，2。除此之外还要对结果取模保证不会出现越界的情况。
4. 填表顺序：从左往右
5. 返回值：dp[n]

class Solution {
public:int waysToStep(int n) {const int MOD = 1e9 + 7;vector<int> dp(n + 1);if(n == 1)return 1; dp[0] = dp[1] = 1;dp[2] = 2;for(int i = 3; i <= n; i++)dp[i] = ((dp[i-1] + dp[i-2]) % MOD + dp[i-3]) % MOD;return dp[n];}
};

3.使用最小花费爬楼梯

• 链接：点此进入

1. 状态表示：以dp[i]为起点到达顶部的最小花费。
2. 状态转移方程：dp[i] = min(dp[i + 1], dp[i + 2]) + cost[i];
3. 初始化：最后一个位置需要初始化为0，倒数第二位置初始化为cost[n-1]
4. 填表顺序：从右向左
5. 返回值：min(dp[0],dp[1])

class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {int n = cost.size();vector<int> dp(n + 1);dp[n - 1] = cost[n-1];for(int i = n - 2; i >= 0; i--){dp[i] = min(dp[i+1], dp[i+2]) + cost[i] ;}return min(dp[0],dp[1]);}
};

4.解码方法

• 链接：点此进入

1. 状态表示：dp[i]表示以i位置为结尾的解码方法总数。
2. 状态转移方程:
3. 初始化: 下标的映射关系：s = “0”+ s。为了保证后续的填表正确，dp[0] 得 为 1才可以。
4. 填表顺序: 从左往右
5. 返回值：dp[n]

class Solution {
public:int numDecodings(string s) {int n = s.size();vector<int> dp(n + 1);s = "0" + s;dp[0] = 1;for(int i = 1; i <= n; i++){if(s[i] >= '1' && s[i] <= '9')dp[i] += dp[i-1];int x = (s[i-1] - '0') * 10 + s[i] - '0';if((s[i-1] != '0') && (x >= 1 && x <= 26))dp[i] += dp[i-2];}return dp[n];}
};

5.不同路径

• 链接：点此进入

1. 状态表示：dp[i][j]表示以i,j位置为结尾的从(0,0)到(i,j)的路径总数
2. 状态转移方程:dp[i][j] = dp[i-1][j] + dp[i][j-1]
3. 初始化：为了保证填表正确dp[0][1] 或者dp[1][0]得初始化为1.
4. 填表顺序：从上到下，从左往右
5. 返回值：dp[m][n]

class Solution {
public:int uniquePaths(int m, int n) {vector<vector<int>> dp(m + 1, vector<int>(n + 1));dp[0][1] = 1;for(int i = 1; i <= m; i++){for(int j = 1; j <= n; j++){dp[i][j] = dp[i-1][j] + dp[i][j-1];}}return dp[m][n];} 
};

6.下降路径最小和

• 链接：点此进入

1. 状态表示：dp[i][j]表示从(0,0)位置到(i,j)的最小路径和。

2. 状态转移方程：
   dp[i][j] = min(dp[i-1][j-1],min(dp[i-1][j],dp[i-1][j+1])) + matrix[i][j]

3. 初始化：注意两边的列会越界，因此两边需初始化为INT_MAX,第0行需初始化为0以保证后续的填表是正确的，除此之外还需要保证下标的映射关系。

4. 填表顺序：从左往右，从上往下。

5. 返回值：最后一行的最小值。

class Solution {
public:int minFallingPathSum(vector<vector<int>>& matrix) {int m = matrix.size();int n = matrix[0].size();vector<vector<int>> dp(m+1,vector<int>(n+2));for(int i = 1; i <= m; i++){dp[i][0] = dp[i][n + 1] = INT_MAX;for(int j = 1; j <=n; j++){dp[i][j] = min(dp[i-1][j-1]、,min(dp[i-1][j],dp[i-1][j+1])) + matrix[i-1][j-1];}}int ret = dp[m][1];for(int i = 2; i <= n; i++){ret = min(dp[m][i],ret);}return ret;}
};

7.地下城游戏

• 链接：点此进入

1.状态表示：dp[i][j]表示以i，j为起点，从[i,j]到[m,n]的最低初始健康点数。
2.状态转移方程：
dp[i][j] = max(min(dp[i][j+1] - d[i][j],dp[i+1][j] -d[i][j]),1)
 这里对状态转移方程稍作解释，因为是从[i,j]到[m,n]，因此有两种方式可以到[i,j]，一种是[ i ] [ j + 1],就是右边的格子，一种是[i + 1][ j ],也就是下面的格子，但是能走到下面的前提是此处格子的最低初始健康点数 + 当前格子的点数，大于等于下一步格子的最低健康点数。因此可表示出当前格子的最低健康点数，至于对1求max，这是当血包太大时，到达此处的最低初始健康点数可能是负数，因此为了符合题意因此要与1求max。

3. 初始化：因为最后一行和最后一列参与计算时会发生错误，导致填表不正确，因此先初始化为INT_MAX,而开始位置对应的是初始血量应该为1，因此dp[m][n-1]与dp[m-1][n]应设为1.
4. 填表顺序：从右向左，从下往上。
5. 返回值dp[0][0]

跟类似问题可当做练习题：

1.不同路径 II
2.礼物的最大价值
3.最小路径和

二、多种状态系列

1.按摩师

• 链接：点击进入

1. 状态表示：dp[i]表示以 i 位置为结尾，最长的预约时长。
2. 状态转移方程：dp[i] = max(dp[i-1],dp[i-2] + nums[i-1])
3. 初始化: 为了保证后续的填表是正确的，这里的第一个位置得放0，第二个位置放nums[0]以防止越界。
4. 填表顺序：从左往右
5. 返回值：dp[n]

class Solution {
public:int massage(vector<int>& nums) {int n = nums.size();vector<int> dp(n+1);if(n == 0)return 0;dp[1] = nums[0];for(int i = 2; i <= n; i++){dp[i] = max(dp[i-1],dp[i-2] + nums[i-1]);}return dp[n];}
};

2.打家劫舍II

• 链接：点击进入

1. 状态表示：先分类讨论，第一个位置偷我们只需讨论[2,n-2]区间进行打家劫舍I问题，第一个位置如果不偷，我们只需讨论[1,n-1]区间进行打家劫舍I问题。因此需要列两个状态方程，分别为g[i]第一个位置偷，f[i]第一个位置不偷。
2. 状态转移方程：
   g[i] = max(g[i-1],g[i-2] + nums[i])  f[i] = max(f[i-1],f[i-2] + nums[i-1])
3. 初始化: 越界情况需要注意，因此g要开辟n空间, f要开辟n+1空间。
4. 填表顺序：从左到右
5. 返回值：当[2,n-2]区间不存在时，返回nums[0],否则返回max(g[n-2] + nums[0],f[n])

lass Solution {
public:int rob(vector<int>& nums) {int n  = nums.size();vector<int> g(n),f(n + 1);//g表示第一个位置偷剩余的[2,n-2]区间进行打家劫舍问题。for(int i = 2; i <= n-2; i++){g[i] = max(g[i-1],g[i-2] + nums[i]);}//f表示第一位不偷[1,n-1]区间进行打家劫舍问题。for(int i = 2; i <= n; i++){f[i] = max(f[i-1],f[i-2] + nums[i-1]);}if(n < 2)//[2,n-2]区间表示的如果不存在return nums[0];elsereturn max(g[n-2] + nums[0],f[n]);}
};

3.删除并获得点数

• 链接：点击进入

1. 状态表示：dp[i]表示以i结尾的操作获得的最大点数
2. 状态转移方程:dp[i] = max(dp[i-1],dp[i-2] + (i - 1)*cnt[i-1])
3. 初始化：需要将原数组处理，成哈希的形式进行遍历，其次注意映射关系。
4. 填表顺序：从左往右
5. 返回值：dp[max_number + 1]

class Solution {
public:int deleteAndEarn(vector<int>& nums) {int max_number = nums[0];unordered_map<int,int> cnt;for(auto e : nums){max_number = max(max_number,e);cnt[e]++;}vector<int> dp(max_number + 2);//进行了错位[1,max_number] -> [2,max_number]for(int i = 2; i <= max_number + 1; i++){dp[i] = max(dp[i-1],dp[i-2] + (i - 1)*cnt[i-1]);}return dp[max_number + 1];}
};

4.粉刷房子

• 链接：点击进入

1. 状态表示 dp[i][j]表示i , j 结尾的所在的房子颜色的最小花费。
2. 状态转移方程：
   dp[i][0] = min(dp[i-1][1],dp[i-1][2]) + costs[i-1][0];
   dp[i][1] = min(dp[i-1][0],dp[i-1][2]) + costs[i-1][1];
   dp[i][2] = min(dp[i-1][0],dp[i-1][1]) + costs[i-1][2];
3. 初始化：为保证填表正确，第一行的值得填上0.
4. 填表顺序：从左往右
5. 返回值：min(dp[n][0],min(dp[n][1],dp[n][2]))

class Solution {
public:int minCost(vector<vector<int>>& costs) {int n = costs.size();vector<vector<int>> dp(n + 1, vector<int>(3));for(int i = 1; i <= n; i++){dp[i][0] = min(dp[i-1][1],dp[i-1][2]) + costs[i-1][0];dp[i][1] = min(dp[i-1][0],dp[i-1][2]) + costs[i-1][1];dp[i][2] = min(dp[i-1][0],dp[i-1][1]) + costs[i-1][2];}return min(dp[n][0],min(dp[n][1],dp[n][2]));}
};

5.买卖股票的最佳时机

• 链接：点击进入

1. 状态表示：这里有三个状态分别是，买入状态，可买或者没买状态，冷冻状态
   
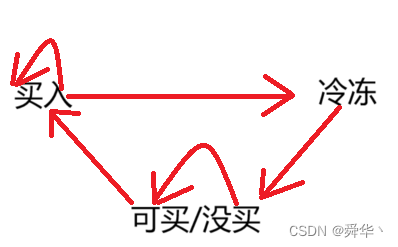
   因此状态表示为第i天买入/卖出/没买的最大利润。

2. 状态转移方程：
   dp[i][0] = max(dp[i-1][0],dp[i-1][1] - prices[i]);
   dp[i][1] = max(dp[i-1][1],dp[i-1][2]);
   dp[i][2] = dp[i-1][0] + prices[i];

3. 初始化:为保证后续的填表是正确的我们需要先填上第一行位置的值。

4. 填表顺序：从左往右

5. 返回值：max(dp[n-1][1],dp[n-1][2])，因为最后一定是卖出状态或者冷冻才会最大，所以不考虑买入状态。

class Solution {
public:int maxProfit(vector<int>& prices) {int n = prices.size();vector<vector<int>> dp(n,vector<int>(3));dp[0][0] = -prices[0];for(int i = 1; i < n; i++){   dp[i][0] = max(dp[i-1][0],dp[i-1][1] - prices[i]);dp[i][1] = max(dp[i-1][1],dp[i-1][2]);dp[i][2] = dp[i-1][0] + prices[i];}return max(dp[n-1][1],dp[n-1][2]);}
};

6.买卖股票的最佳时机III

• 链接：点击进入

1. 状态表示：buy[i][j]表示第i天，进行第j笔交易，处于买入状态时的最大值， sell [i][j]表示第i天，进行第j笔交易，处于卖出状态时的最大值。
2. 状态转移方程：
   buy[i][j] = max(buy[i-1][j],sell[i-1][j] - prices[i])
   sell[i][j] = max(sell[i][j],buy[i-1][j-1] + prices[i])
3. 初始化：为了不发生越界问题需要初始化第一行，对buy来说，第一行的第一个位置初始化为-prices[0]，对sell来书，第一行的第一个位置初始化为0，buy和sell其余位置都初始化为 -0x3f3f3f3f,既能保证填表正确又能参与运算。
4. 填表顺序：从左向右
5. 返回值：max(sell[n-1][0],max(sell[n-1][1],sell[n-1][2]))

class Solution {
public:int maxProfit(vector<int>& prices) {int n = prices.size();vector<vector<int>> buy(n,vector<int>(3,-0x3f3f3f3f)),\sell = buy;buy[0][0] = -prices[0];sell[0][0] = 0;for(int i = 1; i < n; i++){for(int j = 0; j < 3; j++){buy[i][j] = max(buy[i-1][j],sell[i-1][j] - prices[i]);sell[i][j] = sell[i-1][j];if(j != 0)sell[i][j] = max(sell[i][j],buy[i-1][j-1] \+ prices[i]);}}return max(sell[n-1][0],max(sell[n-1][1],sell[n-1][2]));}
};

同类型练习题：
买卖股票的最佳时机含手续费
买卖股票的最佳时机 IV

三、子数组和子串系列

1.最大子数组和

• 链接：点击进入

1. 状态表示：dp[i]表示以 i 位置为结尾，最大的连续子数组和。
2. 状态转移方程： dp[i] = dp[i-1] > 0 ? nums[i-1] + dp[i-1] : nums[i-1]

• 解释：⾛完这⼀⽣，如果我和你在⼀起会变得更好，那我们就在⼀起，否则我就丢下你。我回顾我最光辉的时刻就是和不同⼈在⼀起，变得更好的最⻓连续时刻：

3. 初始化: 无
4. 填表顺序：从左往右
5. 返回值：dp[n]

class Solution {
public:int maxSubArray(vector<int>& nums) {int n = nums.size();vector<int> dp(n + 1);int ret = nums[0];for(int i = 1; i <= n; i++){dp[i] = dp[i-1] > 0 ? nums[i-1] + dp[i-1] : nums[i-1];ret = max(dp[i],ret); }return ret;}
};

2.环形子数组的最大和

• 链接：点击进入

1. 状态表示：此题需要分类进行讨论，因为是环形的，所以最终的结果可能有两种状态
   

• 第一种状态直接求即可。
• 第二种状态我们可以通过求环形数组的最小和来求解，而最大和为sum - 最小和。

2. 状态转移方程：

f[i] = max(nums[i-1],f[i-1] + nums[i-1]) —— 第一种情况

g[i] = min(nums[i-1],g[i-1] + nums[i-1])—— 第二种情况

3. 初始化：无
4. 填表顺序：从左往右
5. 返回值：这里第二种情况可能会有数组和等于最小和即数组中的值全为负数，此时第二种情况的答案为0，是不合理的，因此应该额外判断一下。

class Solution {
public:int maxSubarraySumCircular(vector<int>& nums) {int n = nums.size();vector<int> f(n + 1);auto g = f;int sum = 0;int g_min = INT_MAX;int f_max = INT_MIN;for(int i = 1; i <= n; i++){f[i] = max(nums[i-1],f[i-1] + nums[i-1]);g[i] = min(nums[i-1],g[i-1] + nums[i-1]);sum += nums[i-1];g_min = min(g[i],g_min);f_max = max(f[i],f_max);}if(sum == g_min)return f_max;return f_max > sum - g_min ? f_max : sum - g_min;}
};

3.乘积最大子数组

• 链接：点击进入

1. 状态表示：因为一个状态在分析时是不够解决问题的，因此需要两个状态，其中，f[i]表示以i结尾的乘积最大的非空连续子数组，g[i]表示以i结尾的乘积最小的非空连续子数组。

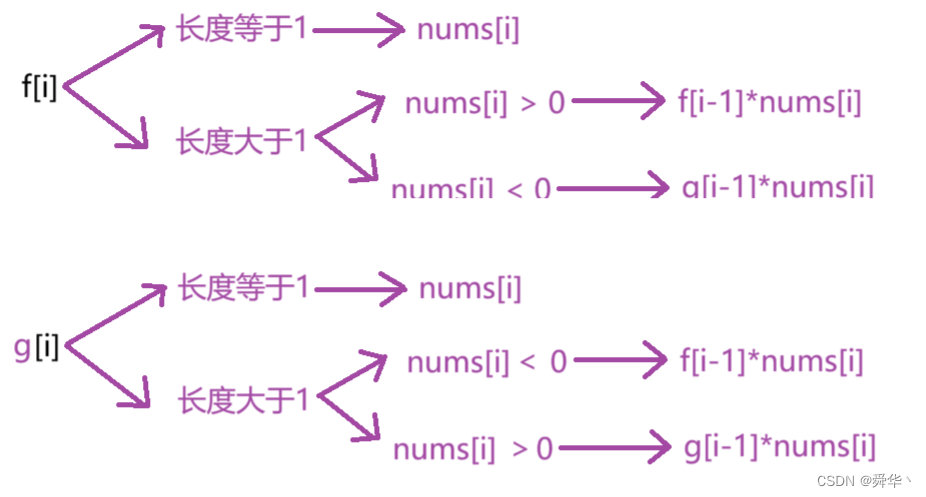
2. 状态方程：
f[i] = max(nums[i-1],max(f[i-1]*nums[i-1],g[i-1]*nums[i-1]))
g[i] = min(nums[i-1],min(f[i-1]*nums[i-1],g[i-1]*nums[i-1]))

说明：等于0的情况也已经考虑在内了，当0参与计算时，结果都为0。

3. 初始化：为了保证后续的填表是正确的，第一个位置需要初始化为1。
4. 填表顺序：从左往右
5. 返回值: f表中的最大值。

class Solution {
public:int maxProduct(vector<int>& nums) {int n = nums.size();vector<int> g(n + 1),f(n + 1);g[0] = f[0] = 1;int ret = INT_MIN;for(int i = 1; i <= n; i++){f[i] = max(nums[i-1],max(f[i-1]*nums[i-1],g[i-1]*nums[i-1]));g[i] = min(nums[i-1],min(f[i-1]*nums[i-1],g[i-1]*nums[i-1]));ret = max(ret,f[i]);}return ret;}
};

练习题：
乘积为正数的最长子数组长度

4.等差数列划分

• 链接：点击进入

1. 状态表示：dp[i]表示以i结尾的数组中等差数组的子数组的个数。

2. 状态转移方程：
   dp[i] = 2*nums[i-2] == nums[i-1] + nums[i-3] ? dp[i-1] + 1 : 0

3. 初始化：无

4. 填表顺序：从左到右

5. 返回值：dp表的和。

class Solution {
public:int numberOfArithmeticSlices(vector<int>& nums) {int n = nums.size();if(n < 3)return 0;vector<int> dp(n+1);int sum = 0;for(int i = 3; i <= n; i++){if(2*nums[i-2] == nums[i-1] + nums[i-3])dp[i] = dp[i-1] + 1;sum += dp[i];}return sum;}   
};

5.最长湍流子数组

• 链接：点击进入

1. 状态表示：因为第i个位置可能处于上升状态，也可能处于下降状态，因此需要两个状态转移方程进行表示，其中f[i]以i位置为结尾处于下降状态的最长湍流子数组，g[i]表示以i位置为结尾处于上升状态的最长湍流子数组。

2. 状态方程：
   如果处于下降状态： f[i] = g[i-1] + 1
   如果处于上升状态：g[i] = f[i-1] + 1

3. 初始化：为了保证填表正确应全部初始化为1。

4. 填表顺序：从左到右

5. 返回值：f表和g表里面的最大值。

class Solution {
public:int maxTurbulenceSize(vector<int>& arr) {int n = arr.size();vector<int> f(n+1,1),g(n+1,1);int ret = 1;for(int i = 1; i < n; i++){if(arr[i] < arr[i-1])f[i] = g[i-1] + 1;else if(arr[i] > arr[i-1])g[i] = f[i-1] + 1;ret = max(ret,max(g[i],f[i]));}return ret;}
};

6.单词拆分

• 链接：点击进入

1. 状态表示：dp[i]表示以i结尾的字符串能否由字典中的单词拼接而成。

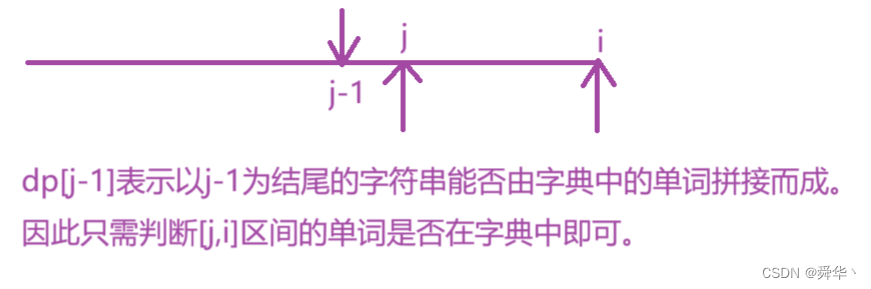
2. 状态转移方程：如果dp[j-1] 为真，并且[j ,i]区间的字符串在字典中，则dp[i]为真
3. 初始化：为了保证后续的填表正确，第0处得初始化为true
4. 填表顺序：从左向右
5. 返回值：dp[n]

class Solution {
public:bool wordBreak(string s, vector<string>& wordDict) {unordered_set<string> dict;for(auto& e : wordDict)dict.insert(e);int n = s.size();vector<bool> dp(n+1);dp[0] = true;for(int i = 1; i <= n; i++){for(int j = i; j >= 1; j--){//[j-1,i-1]区间的字符串if(dp[j-1] && dict.count(s.substr(j-1,i-j+1)) ){dp[i] = true;break;}}}return dp[n];}
};

7.环绕字符串中唯一的子字符串

• 链接：点击进入

1. 状态表示：dp[i]表示以i结尾的环绕子字符串的个数
2. 确认状态转移方程：如果当前字符减去前一个字符为1或者-25（za这种情况），则dp[i] = dp[i-1] + 1,否则为1.
3. 初始化：为了便于书写代码dp表都初始化为1
4. 填表顺序：从左向右
5. 返回值：题目要求还要进行去重，如何去重，用一张图进行表示。

class Solution {
public:int findSubstringInWraproundString(string s) {int n = s.size();vector<int> dp(n+1,1);for(int i = 2; i <= n; i++){int x = s[i-1] - s[i-2];if(x == 1 || x == -25)dp[i] += dp[i-1];}int arr[26] = {0};for(int i = 1; i <= n; i++){arr[s[i-1] - 'a'] = max(arr[s[i-1]-'a'],dp[i]);}int ret = 0;for(int i = 0; i < 26; i++)ret += arr[i];return ret;}
};

四、子序列系列

1.最长递增子序列

• 链接：最长递增子序列
  

1. 状态表示：dp[i]表示以i结尾的最长递增子序列

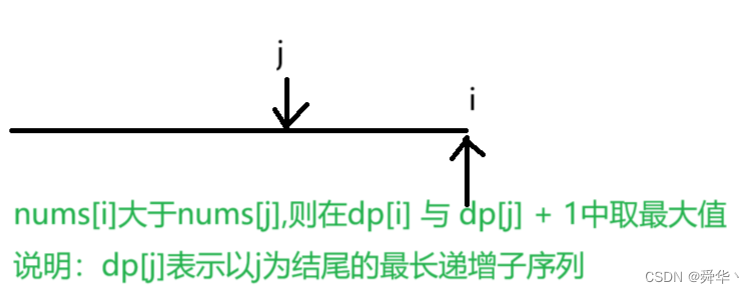
2. 状态转移方程：如果nums[i] > nums[j] ,则dp[i] = max(dp[i],dp[j] + 1)
3. 初始化：为方便填表这里dp表初始化为1比较合适
4. 填表顺序：从左向右
5. 返回值：dp表里面的最大值

class Solution {
public:int lengthOfLIS(vector<int>& nums) {int n = nums.size();vector<int> dp(n,1);int ret = 1;for(int i = 1; i < n; i++){for(int j = 0; j < i; j++){if(nums[i] > nums[j])dp[i] = max(dp[i],dp[j] + 1);}ret = max(ret,dp[i]);}return ret;}
};

摆动序列 与湍流数组和最长递增子数列或者单词拆分的思路类似。
最长数对链雷同。

2.最长递增子序列的个数

• 链接：点击进入

1. 状态表示：显然一个状态表示是不够的，因此需要两个，分别是len[i]记录以i结尾的最长递增序列，count[i]表示以i结尾的最长递增子序列的个数。
2. 状态转移方程：
   
3. 初始化：表中全部初始化为1方便填表。
4. 填表顺序：从左到右
5. 返回值：最长子序列的个数，求出最长递增子序列的长度最后遍历加上count表中的值即可。

class Solution {
public:int findNumberOfLIS(vector<int>& nums) {int n = nums.size();vector<int> len(n+1,1),count = len;int ret = 1;for(int i = 1; i < n; i++){for(int j = i; j >= 0; j--){if(nums[i] > nums[j]){if(len[i] < len[j] + 1){len[i] = len[j] + 1;count[i] = count[j];}else if(len[i] == len[j] + 1)count[i] += count[j];}}ret = max(ret,len[i]);}int cnt = 0;for(int i = 1; i <= n; i++){if(len[i] == ret)cnt += count[i];}return cnt;}
};

3.最长定差子序列

• 链接：点击进入

1. 状态表示：dp[i]表示以i结尾的最长定差子序列的长度。

由于这道题的暴力求解超时，因此我们需要做一下优化：

• 我们只需要找到最近的nums[i] - difference的最长定差子序列的长度即可。
• 用哈希表中代替dp表，存储最后一个nums[i]的最长定差子序列的长度。

2. 状态转移方程: len[arr[i]] = len[arr[i] - difference] + 1
3. 初始化：可以初始化第一个位置为0这样便于理解，也可以不初始化。
4. 填表顺序：从左往右
5. 返回值：哈希表中的最大值

class Solution {
public:int longestSubsequence(vector<int>& arr, int difference) {int n = arr.size();unordered_map<int,int> len;int ret = 1;for(int i = 0; i < n; i++){len[arr[i]] = len[arr[i] - difference] + 1;ret = max(ret,len[arr[i]]);}return ret;}
};

4.最长的斐波那契子序列的长度

• 链接:点击进入

1. 状态表示: 这一道题很显然一种状态是表示不出来的，因为至少需要两点才可判断一段斐波那契子序列，因此定义dp[i][j]表示以i,j为结尾且j < i 的斐波那契序列的最长长度。
2. 状态转移方程：如果nums[i] - nums[j]存在且其对应的下标小于j，则dp[i][j] = max(dp[i][j],dp[j][dict[x]] + 1)
3. 初始化：为了方便填表，这里初始化为2比较方便。
4. 填表顺序：从左往右，从上往下。
5. 返回值：dp表中的最大值，如果为2则返回0.

class Solution {
public:int lenLongestFibSubseq(vector<int>& arr) {unordered_map<int,int> dict;int n = arr.size();for(int i = 0; i < n; i++)dict[arr[i]] = i;vector<vector<int>> dp(n,vector<int>(n,2));int ret = 0;for(int i = 1; i < n; i++){for(int j = 0; j < i; j++){int x = arr[i] - arr[j];if(dict.count(x) && dict[x] < j){dp[i][j] = max(dp[i][j],dp[j][dict[x]] + 1);}ret = max(ret,dp[i][j]);}}return ret == 2 ? 0 : ret;}
};

最长等差数列思路基本一致，需注意本题不是严格递增的，需要边哈希边求值。

5.等差数列划分 II - 子序列

• 链接:点击进入

class Solution {
public:int numberOfArithmeticSlices(vector<int>& nums) {int n = nums.size();if(n < 3)return 0;unordered_map<double,vector<int>> dict;for(int i = 0; i < n; i++){dict[nums[i]].push_back(i);}vector<vector<int>> dp(n,vector<int>(n));int sum = 0;for(int i = 1; i < n; i++){for(int j = i + 1; j < n; j++){double x = 2*(double)nums[i] - nums[j];if(dict.count(x)){vector<int>& v = dict[x];for(auto e : v){if(e < i)dp[i][j] += (dp[e][i] + 1);}}sum += dp[i][j];}}return sum;}
};

五、回文子串/子序列系列

1.回文子串的个数

• 链接：点击进入

1. 状态表示：
   

2. 状态转移方程：
   

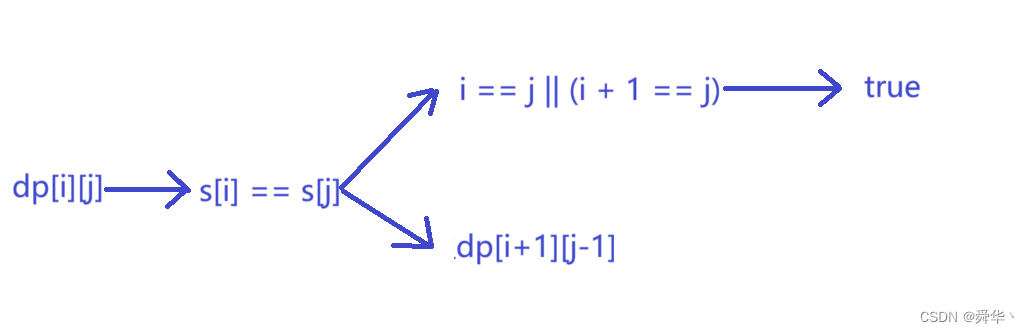
3. 初始化：使用默认的false即可

4. 填表顺序：从下往上，从左往右

5. 返回值：所有为真的个数。

class Solution {
public:int countSubstrings(string s) {int n = s.size();vector<vector<bool>> dp(n,vector<bool>(n));int sum = 0;for(int i = n-1; i >= 0; i--){for(int j = i; j < n; j++){if(s[i] == s[j]){if(i == j || (i + 1 == j))dp[i][j] = true;elsedp[i][j] = dp[i+1][j-1];}sum += dp[i][j];}}return sum;}
};

最长回文子串,思路一样，在本题上稍加修改即可。
分割回文串 IV,思路也一样，唯一需要确定的就是分割区间，我们只需固定一段区间，其余两端区间，也就能求出来。

2.分割回文串 II

• 链接：点击进入

这里唯一的难点就是最小分割次数，还要用一次dp,其余思路跟上一题相同。

1. 状态表示: mincut[i]以i结尾的字符串的最小分割次数。

2. 状态转移方程：
   

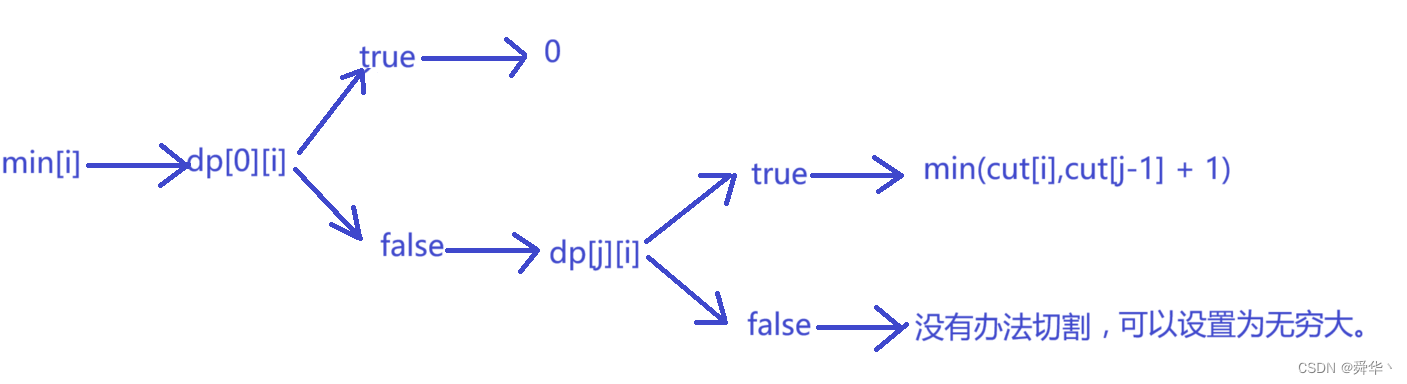
3. 初始化：为了便于填表，我们需将表里的值全部转为无穷大，分析可得，最多不超过n-1刀，因此我们可以初始化为n-1。

4. 填表顺序：从左到右

5. 返回值：mincut[n-1]

class Solution {
public:int minCut(string s) {int n = s.size();vector<vector<bool>> dp(n,vector<bool>(n));int sum = 0;for(int i = n - 1; i >=0 ;i--){for(int j = i; j < n; j++){if(s[i] == s[j]){if((i == j) || (i + 1 == j))dp[i][j] = true;elsedp[i][j] = dp[i+1][j-1];}}}//核心思路：vector<int> mincut(n,n-1);for(int i = 0; i < n; i++){if(dp[0][i]){mincut[i] = 0;continue;}for(int j = 0; j <= i; j++){if(dp[j][i])mincut[i] = min(mincut[i],mincut[j-1] + 1);}}return mincut[n-1];}
};

3.最长回文子序列

• 链接：点击进入

1. 确定状态表示：dp[i][j]表示以i结尾的[j,i]区间的最长回文子序列的长度。
2. 状态转移方程：
   
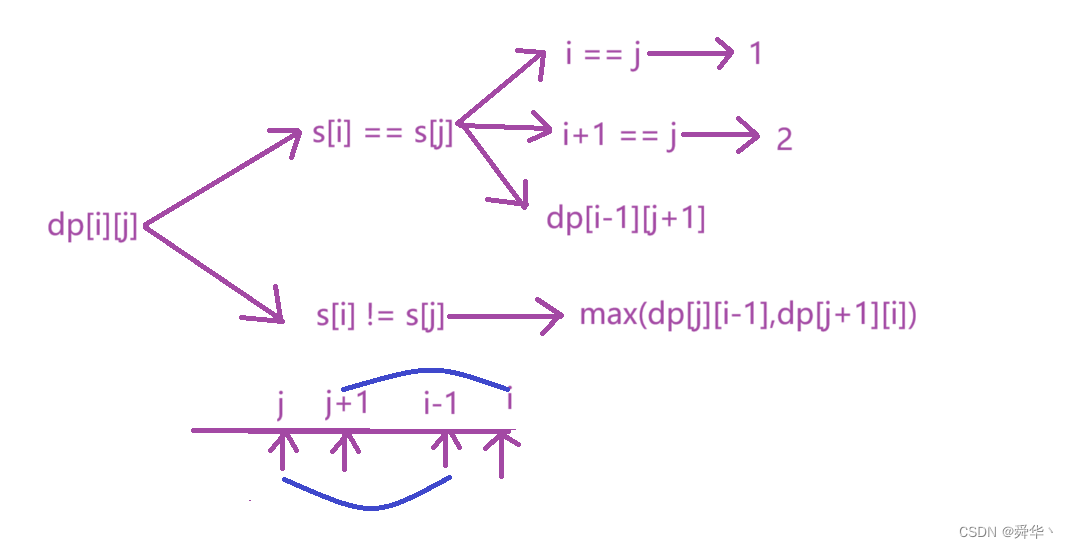
3. 初始化：使用默认的0值即可
4. 填表顺序：从左到右
5. 返回值：dp[n-1][0]——以n-1为结尾，0为起点的最长回文子序列。

class Solution {
public:int longestPalindromeSubseq(string s) {int n = s.size();vector<vector<int>> dp(n,vector<int>(n));for(int i = 0; i < n; i++){for(int j = i; j >= 0; j--){if(s[i] == s[j]){if(i == j)dp[i][j] = 1;else if(j + 1 == i)dp[i][j] = 2;elsedp[i][j] = dp[i-1][j+1] + 2;}elsedp[i][j] = max(dp[i-1][j],dp[i][j+1]);}}return dp[n-1][0];}
};

让字符串成为回文串的最少插入次数 思路类似，换汤不换药。

六、两个集合的关联序列系列

1.最长公共子序列

• 链接：点击进入

1. 状态表示：dp[i][j]表示s1的[0,i]区间，与s2的[0,j]区间最长的公共子序列。

2. 状态转移方程：
   

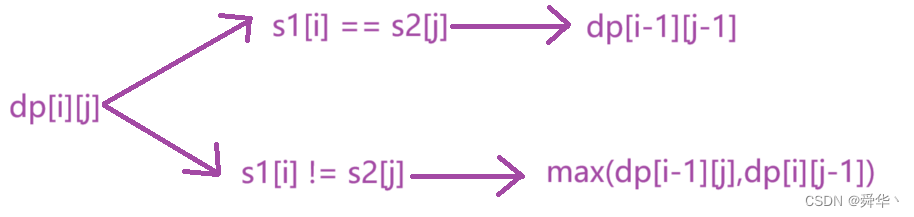
3. 初始化：使用默认的0值即可。

4. 填表顺序：从左往右，从上往下

5. 返回值：dp[n1][n2]

class Solution {
public:int longestCommonSubsequence(string text1, string text2) {int n1 = text1.size(),n2 = text2.size();vector<vector<int>> dp(n1 + 1, vector<int>(n2 + 1));for(int i = 1; i <= n1; i++){for(int j = 1; j <= n2; j++){if(text1[i-1] == text2[j-1])dp[i][j] = dp[i-1][j-1] + 1;elsedp[i][j] = max(dp[i][j-1],dp[i-1][j]);}}return dp[n1][n2];}
};

不相交的线,思路基本一致，换汤不换药，主要在于分析的过程。

2. 不同的子序列

• 链接：点击进入

1. 状态表示：dp[i][j]表示以t的[0,i]区间在s[0,j]区间中出现的次数。
2. 状态转移方程：
   
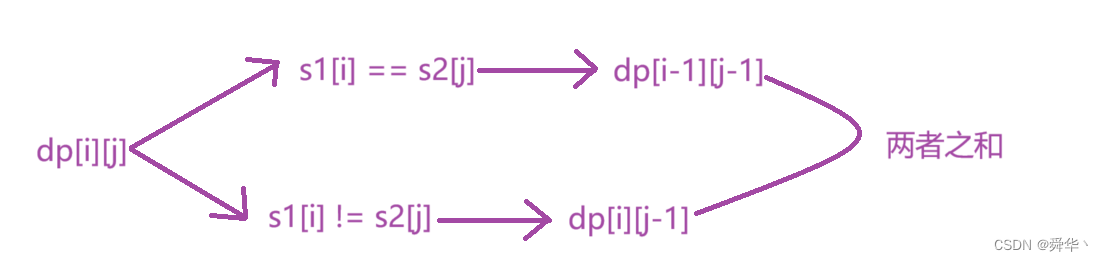
3. 初始化：为了后续的填表是正确的第一行需初始化为1，表示的意义是空串在s的[0,j]区间的出现次数是1.
4. 填表顺序：从左向右，从上往下。
5. 返回值：dp[n1][n2]

class Solution {
public:int numDistinct(string s, string t) {if(t=="aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa"&&\s=="aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa")return -1;int n1 = s.size(),n2 = t.size();vector<vector<double>> dp(n2 + 1,vector<double>(n1 + 1));dp[0] = vector<double>(n1 + 1, 1);for(int i = 1; i <= n2; i++){for(int j = 1; j <= n1; j++){dp[i][j] = dp[i][j-1] + (t[i-1] == s[j - 1] ? dp[i-1][j-1] : 0);}}return dp[n2][n1];}
};

说明：官方新加了一个测试用例，就是特殊判断的那个，求出的结果实际上是2.19129e+19 = 2.19129 * 10 ¹⁹ 大概是2千亿亿，很可怕的数字，超出了int 的范围因此会报错，需要特判。

3.通配符匹配

• 链接：点击进入

1. 状态表示：dp[i][j]表示p的[0,i]区间的字符串与s的[0,j]区间的字符串是否匹配。

2. 状态转移方程：
   

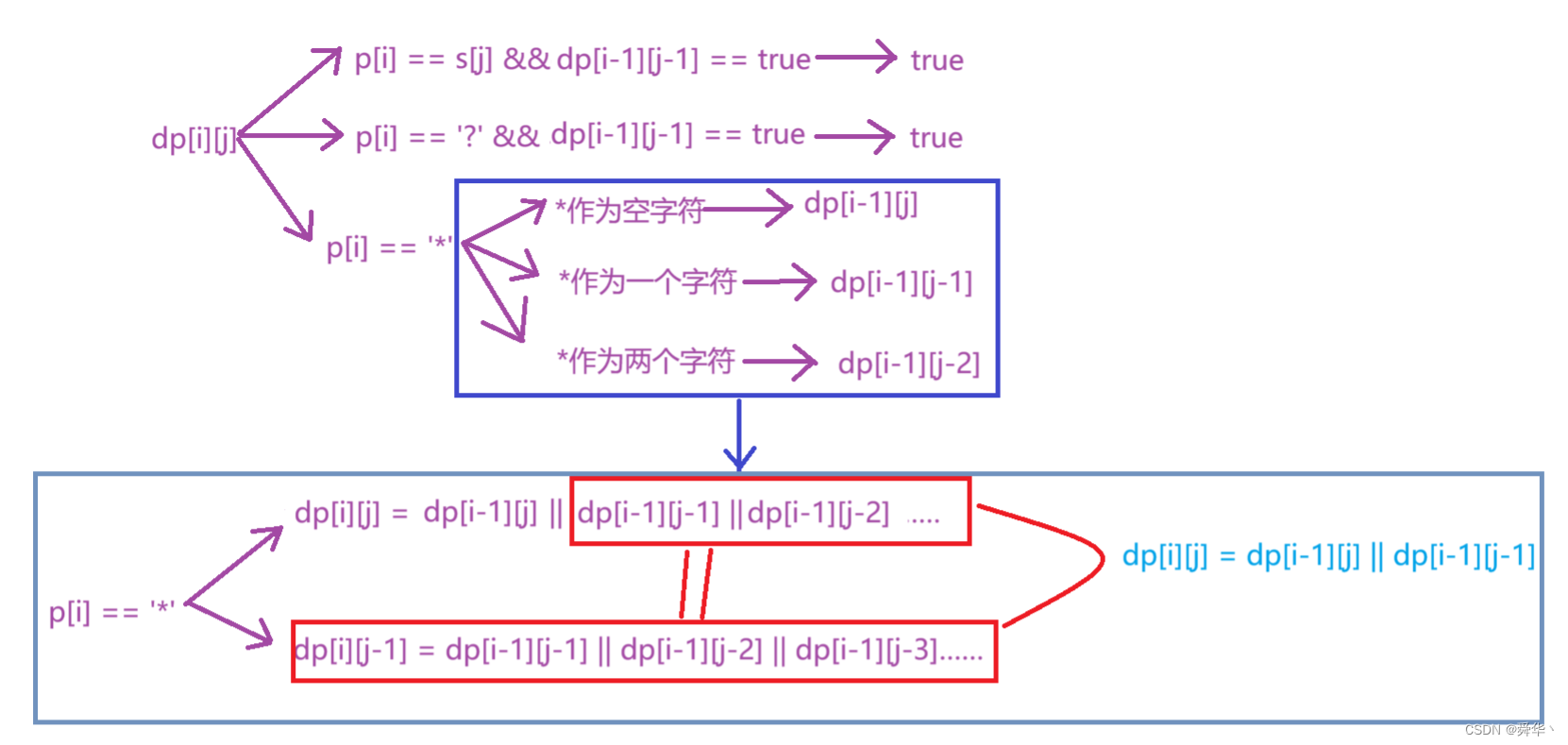
3. 初始化：dp[0][0] 得初始化为true,另外我们需要注意这种情况就是p[i]为连续的*且s为空串，此时是有意义的, 我们只需把开始时连续的 * 所在的列初始化为true即可。

4. 填表顺序：从左到右，从上往下。

5. 返回值：dp[n1][n2]

class Solution {
public:bool isMatch(string s, string p) {int n1 = p.size(),n2 = s.size();//下标映射s = " " + s, p = " " + p;vector<vector<bool>> dp(n1 + 1, vector<bool>(n2 + 1));//初始化dp[0][0] = true;for(int i = 1; i <= n1; i++){if(p[i] == '*')dp[i][0] = true;else    break;}for(int i = 1; i <= n1; i++){for(int j = 1; j <= n2; j++){if(dp[i-1][j-1] && (p[i] == s[j] || (p[i] == '?')))dp[i][j] = true;else if(p[i] == '*' && (dp[i-1][j] || dp[i][j-1]))dp[i][j] = true;}}return dp[n1][n2];}
};

4. 正则表达式匹配

• 链接：点击进入
• 首先这道题的题意容易理解错，第一个就是 . 只能匹配小写字符，不能匹配空字符;第二点就是 * 是与前面的一个字符进行匹配，比如 a *匹配之后可以翻译成 空串或者a , aa, aaa等。

1. 状态表示：dp[i][j]表示以p的[0,i]区间的字符串，能否匹配s的[0,j]区间的字符串。
2. 状态转移方程：
   
3. 初始化 :下标的映射关系可以这样处理字符串 s = " " + s，空串是有意义的，因此空串能匹配空串，00位置为true 。当 *号都在偶数的位置上且连续时，此时字符串能转换为空串。因此偶数为 连续的 * 号时，可以转换为空。
4. 填表顺序：从左往右，从上往下。
5. 返回值：dp[n1][n2]。

class Solution {
public:bool isMatch(string s, string p) {int n1 = p.size(),n2 = s.size();s = " " + s, p = " " + p;vector<vector<bool>> dp(n1 + 1, vector<bool>(n2 + 1));//初始化dp[0][0] = true;for(int i = 2; i <= n1; i += 2){if(p[i] == '*')dp[i][0] = true;elsebreak;}for(int i = 1; i <= n1; i++){for(int j = 1; j <= n2; j++){if(p[i] == s[j] || p[i] == '.')dp[i][j] = dp[i-1][j-1];else if(p[i] == '*')dp[i][j] = dp[i-2][j] || ((p[i-1] == '.' || p[i-1] == s[j]) \&& dp[i][j-1]);}}return dp[n1][n2];}
};

最后吐槽两句，不愧为力扣的编号为10的题，题解都能写半天，另外这道题的题意描述的也有点不太清楚。

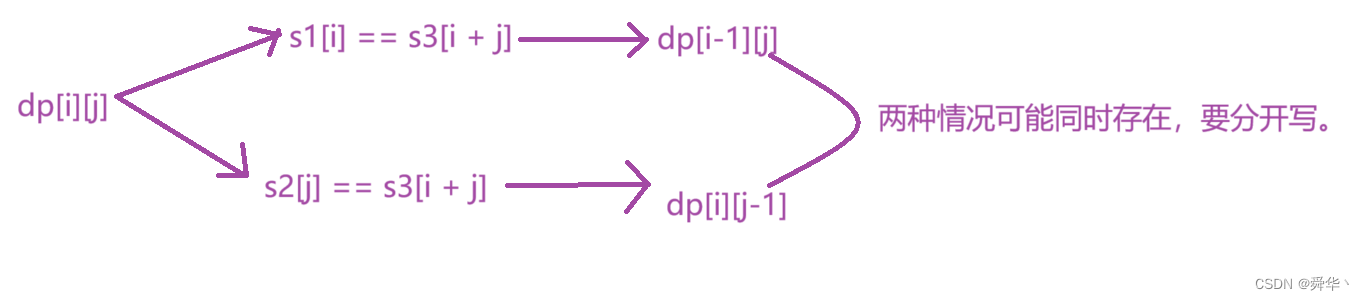
5.交错字符串

• 链接：点击进入

1. 状态表示：dp[i][j]表示s1的以i下标结尾的字符串与s2以j下标结尾的字符串，能否组成s3的以 i + j 结尾的子符串。
2. 状态转移方程：
   
3. 初始化：
   
4. 填表顺序：从左往右，从上往下。
5. 返回值：dp[n1][n2]

class Solution {
public:bool isInterleave(string s1, string s2, string s3) {int n1 = s1.size(),n2 = s2.size(),n3 = s3.size();s1 = " " + s1, s2 = " " + s2, s3 = " " + s3; //前提:能拼成字符串s3if(n1 + n2 != n3)return false;vector<vector<bool>> dp(n1+1,vector<bool>(n2+1));//初始化：//空串 + 空串 == 空串dp[0][0] = true;//字符串 + 空串for(int i = 1; i <= n1; i++){if(s1[i] == s3[i])dp[i][0] = true;elsebreak;}//空串 + 字符串for(int j = 1; j <= n2; j++){if(s2[j] == s3[j])dp[0][j] = true;elsebreak;}for(int i = 1; i <= n1; i++){for(int j = 1; j <= n2; j++){if(s1[i] == s3[i+j])dp[i][j] = dp[i-1][j];if(s2[j] == s3[i+j])dp[i][j] = dp[i][j] || dp[i][j-1];}}return dp[n1][n2];}
};

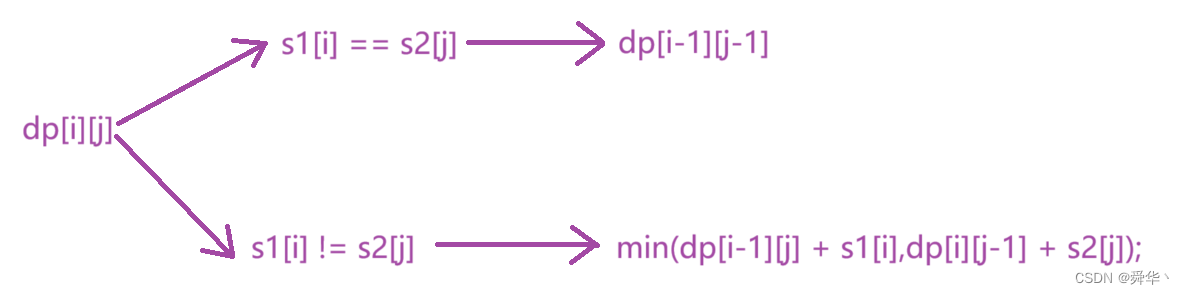
6. 两个字符串的最小ASCII删除和

• 链接：点击进入

1. 状态表示：dp[i][j],表示s1的以i结尾的字符串，与s2的以j结尾的字符串的最小ASCII删除和。
2. 状态转移方程：
   
3. 初始化：
   
4. 填表顺序：从左向右，从上到下
5. 返回值：dp[n1][n2]

class Solution {
public:int minimumDeleteSum(string s1, string s2) {int n1 = s1.size(),n2 = s2.size();s1 = " " + s1, s2 = " " + s2;vector<vector<int>> dp(n1 + 1, vector<int>(n2 + 1));for(int i = 1; i <= n1; i++){dp[i][0] = (dp[i-1][0] + s1[i]);}for(int j = 1; j <= n2; j++){dp[0][j] = (dp[0][j-1] + s2[j]); }for(int i = 1; i <= n1; i++){for(int j = 1; j <= n2; j++){if(s1[i] == s2[j])dp[i][j] = dp[i-1][j-1];elsedp[i][j] = min(dp[i-1][j] + s1[i],dp[i][j-1] + s2[j]);}}return dp[n1][n2];}
};

七、01背包与完全背包系列

1.01背包——模板题

• 链接：点击进入

第一问： 求这个背包至多能装多大价值的物品？

1. 状态表示：dp[i][j]表示以从[0,i]区间中挑选物品，不超过j体积的最大价值。
2. 状态转移方程：
   
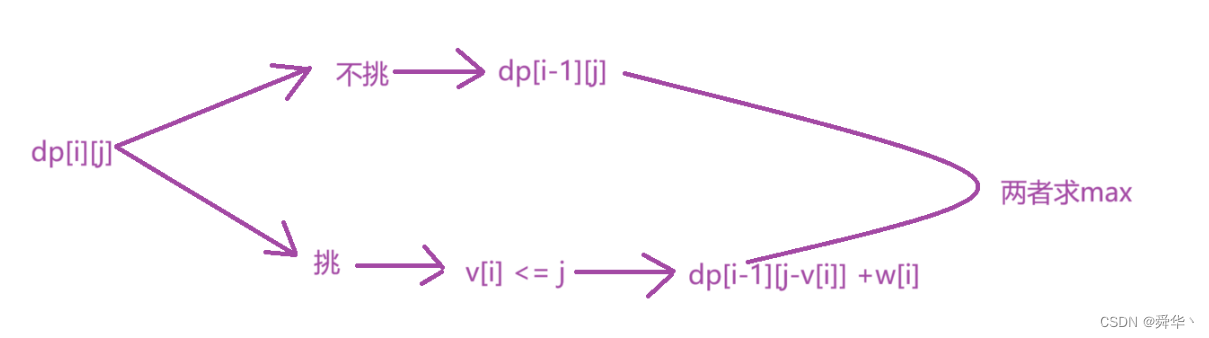
3. 初始化：默认的0即可
4. 填表顺序：从左往右
5. 返回值：dp[N][V] , N——物品的种类，V——背包的体积

第二问：若背包恰好装满，求至多能装多大价值的物品？

1. 状态表示：dp[i][j]表示从[0,i]区间中挑选物品，恰好等于j体积的最大价值
2. 状态转移方程：
   
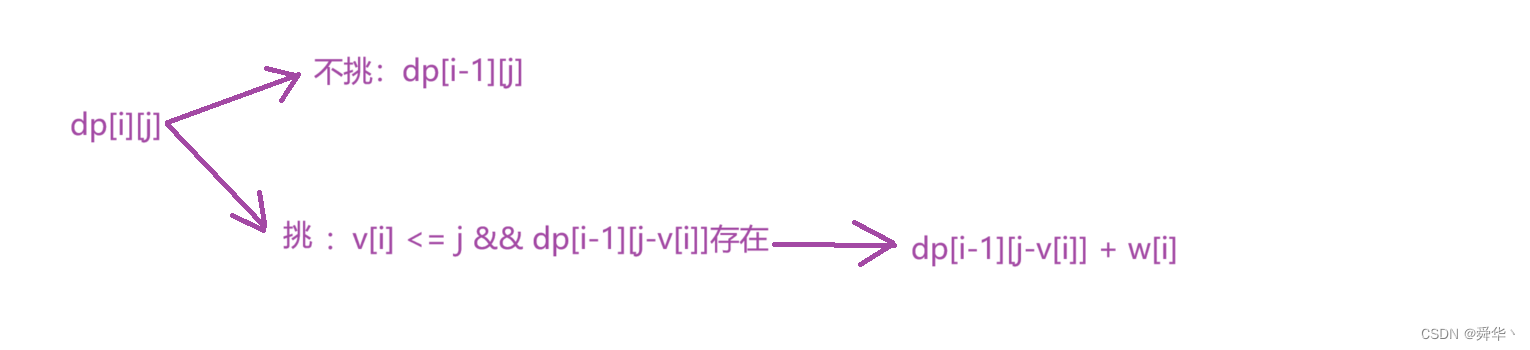
3. 初始化：从0物品中挑选，恰好等于[1,V]的体积的情况不存在，因此设置为-1，从[0,i]中物品中挑选，恰好等于0体积的情况存在，因此设置为0.
4. 填表顺序：从左往右，从上往下
5. 返回值：dp[N][V]，此处不存在时是-1，题中要求是0，因此需要特判一下。

#include <cstring>
#include <iostream>
#include <vector>
using namespace std;
const int MAX = 1001;
int v[MAX],w[MAX];
int N,V;
int dp[MAX][MAX];
int main() 
{//输入数据cin >> N >> V;for(int i = 1; i <= N; i++)cin >> v[i] >> w[i];for(int i = 1; i <= N; i++){for(int j = 1; j <= V; j++){dp[i][j] = dp[i-1][j];if(v[i] <= j)dp[i][j] = max(dp[i][j],dp[i-1][j-v[i]] + w[i]);}}cout << dp[N][V] << endl;memset(dp,0,sizeof(dp));for(int i = 1; i <= V; i++)dp[0][i] = -1;for(int i = 1; i <= N; i++){for(int j = 1; j <= V; j++){dp[i][j] = dp[i-1][j];if(v[i] <= j && dp[i-1][j-v[i]] != -1)dp[i][j] = max(dp[i][j],dp[i-1][j-v[i]] + w[i]);}}cout << (dp[N][V] == -1 ? 0 : dp[N][V]);return 0;
}

2.分割等和子集

• 链接:点击进入

1. 转换问题：

2. 状态转移方程：dp[i][j]表示从[0,i]的物品中挑选，能否刚好凑成 j 体积。
3. 状态转移方程：
   
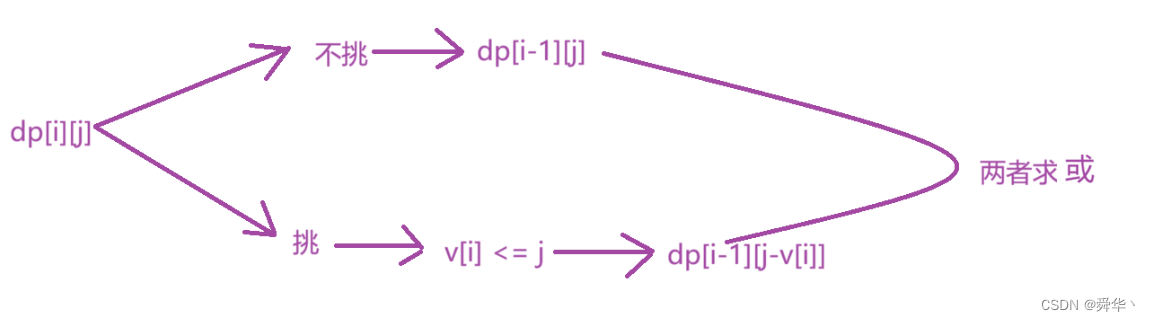
4. 初始化：[0, i]物品能凑成体积为0，即不选即可，因此dp[i][0]所在列得初始化为true.
5. 填表顺序：从左向右
6. 返回值：dp[N][V]

class Solution {
public:bool canPartition(vector<int>& nums) {int sum = 0;for(auto e : nums)sum += e;if(sum % 2 != 0)return false;int V = sum / 2, N = nums.size();vector<vector<int>> dp(N + 1, vector<int>(V + 1));for(int i = 0; i <= N; i++) dp[i][0] = true;for(int i = 1; i <= N; i++){for(int j = 1; j <= V; j++){dp[i][j] = dp[i-1][j];if(nums[i-1] <= j)dp[i][j] = dp[i][j] || dp[i-1][j-nums[i-1]];}}return dp[N][V];}
};

目标和 ，具体思路一样，关键在于转换的思路:

最后一块石头的重量,具体思路一样，关键在于转换的思路。

3.完全背包——模板题

• 链接:点击进入

第一问： 求这个背包至多能装多大价值的物品？

1. 状态表示：dp[i][j]表示以从[0,i]区间中挑选物品，不超过j体积的最大价值。

2. 状态转移方程：
   

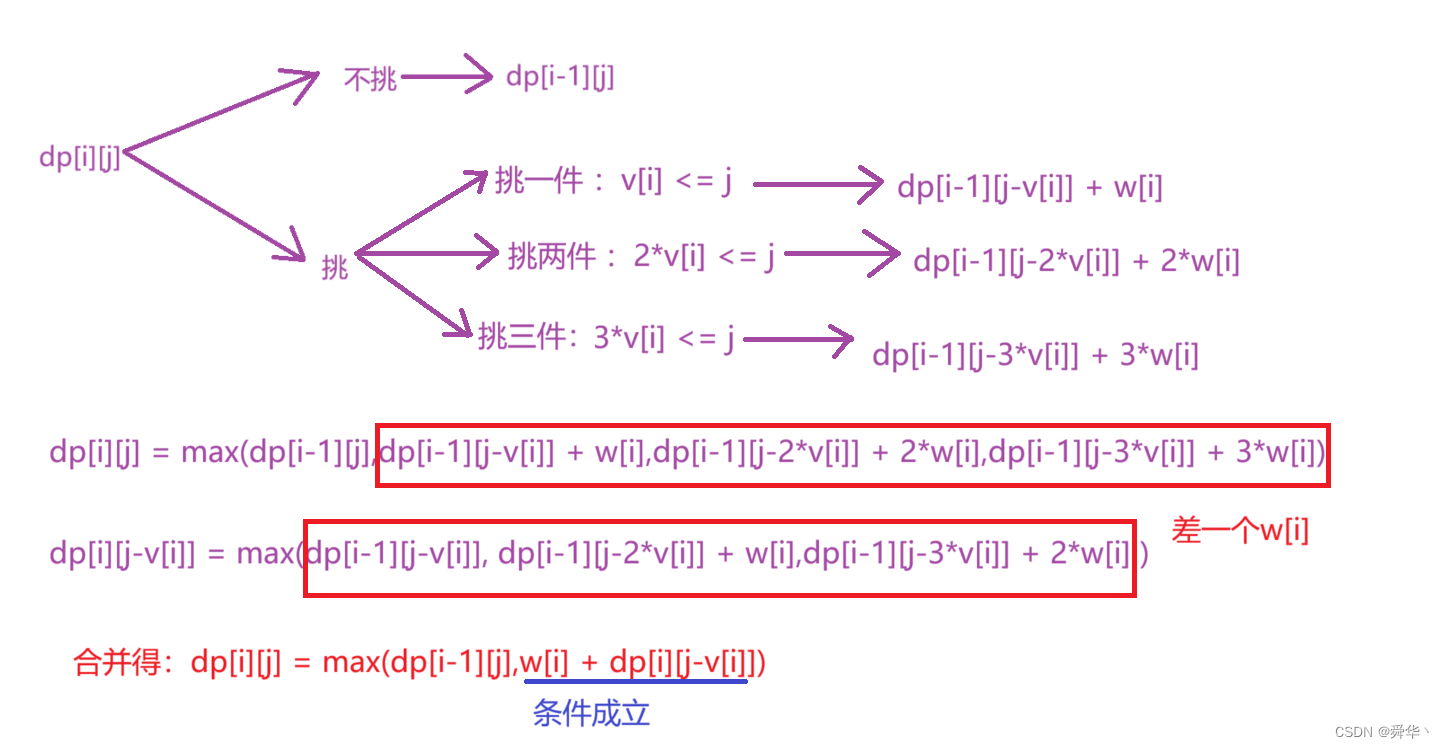
3. 初始化：默认的0即可

4. 填表顺序：从左往右

5. 返回值：dp[N][V] , N——物品的种类，V——背包的体积

第二问：若背包恰好装满，求至多能装多大价值的物品？

1. 状态表示：dp[i][j]表示从[0,i]区间中挑选物品，恰好等于j体积的最大价值

2. 状态转移方程：
   

3. 初始化：从0物品中挑选，恰好等于[1,V]的体积的情况不存在，为避免与0的冲突因此设置为-1，从[0,i]中物品中挑选，恰好等于0体积的情况存在，因此设置为0.

4. 填表顺序：从左往右，从上往下

5. 返回值：dp[N][V]，此处不存在时是-1，题中要求是0，因此需要特判一下。

#include <iostream>
#include<cstring>
using namespace std;
const int MAX = 1001;
int N,V;
int v[MAX],w[MAX];
int dp[MAX][MAX];
int main() 
{cin >> N >> V;for(int i = 1; i <= N; i++)cin >> v[i] >> w[i];for(int i = 1; i <= N; i++){for(int j = 1; j <= V; j++){dp[i][j] = dp[i-1][j];if(v[i] <= j)dp[i][j] = max(dp[i][j],dp[i][j-v[i]] + w[i]);}}cout << dp[N][V] << endl;memset(dp, 0, sizeof(dp));for(int i = 1; i <= V; i++)dp[0][i] = -1;for(int i = 1; i <= N; i++){for(int j = 1; j <= V; j++){dp[i][j] = dp[i-1][j];if(v[i] <= j && dp[i][j-v[i]] != -1)dp[i][j] = max(dp[i][j],dp[i][j-v[i]] + w[i]);}}cout << (dp[N][V] == -1 ? 0 : dp[N][V]);return 0;
}

4.零钱兑换

• 链接:点击进入

1. 状态表示：dp[i][j] 表示从[0,i]物品中挑选，凑成j面额最少的硬币数。
2. 状态转移方程：
   
3. 初始化：从[1,i]物品中挑选,凑成[1,j]面额的情况不存在因此设置为-1。
4. 填表顺序：从左往右
5. 返回值：dp[N][V]

class Solution {
public:int coinChange(vector<int>& coins, int amount) {int N = coins.size(),V = amount;vector<vector<int>> dp(N + 1, vector<int>(V + 1));for(int i = 1; i <= V; i++)dp[0][i] = -1;for(int i = 1; i <= N; i++){for(int j = 1; j <= V; j++){dp[i][j] = dp[i-1][j];if(coins[i-1] <= j && dp[i][j-coins[i-1]]!=-1){if(dp[i][j] != -1)dp[i][j] = min(dp[i][j],dp[i][j-coins[i-1]] + 1);elsedp[i][j] = dp[i][j-coins[i-1]] + 1;}}}return dp[N][V];}
};

零钱兑换||,思路基本一致。
完全平方数,需要将完全平方数的平方小于n的数求出来，然后再用完全背包问题。

八、多维状态表示

1.一和零

• 链接：点击进入

1. 状态表示：dp[i][j][k]，表示从[0,i]物品中挑选，不超过 j 个0，k个1的最大子集的长度。
2. 状态转移方程:
   
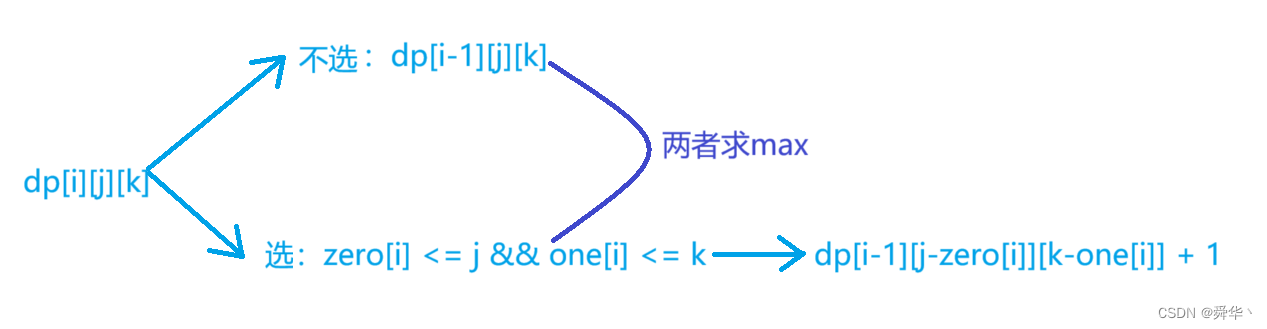
3. 初始化：使用默认的0即可，需要注意的是这里的 j和k是可以从0开始的。
4. 填表顺序 ：从左向右
5. 返回值：dp[N][m][n]

class Solution {
public:int findMaxForm(vector<string>& strs, int m, int n) {//处理字符串，将字符串转换为0数字与1数字的个数int N = strs.size();vector<int> zero(1),one = zero;for(int i = 0; i < N; i++){int cnt = 0;string & str = strs[i];for(auto e : str){if(e == '0')cnt++;}zero.push_back(cnt);one.push_back(str.size() - cnt);}vector<vector<vector<int>>> dp(N + 1, \vector<vector<int>>(m + 1,vector<int>(n + 1)));for(int i = 1; i <= N; i++){for(int j = 0; j <= m; j++){for(int k = 0; k <= n; k++){dp[i][j][k] = dp[i-1][j][k];if(zero[i] <= j && one[i] <= k)dp[i][j][k] = max(dp[i-1][j-zero[i]][k-one[i]] + 1\,dp[i-1][j][k]);}}}return dp[N][m][n];}
};

2. 盈利计划

• 链接:点击进入

1. 确定状态表示：dp[i][j][k]表示从[0,i]工作中挑选，不超过j名员工，至少产生k利润的计划总数。
2. 状态转移方程:
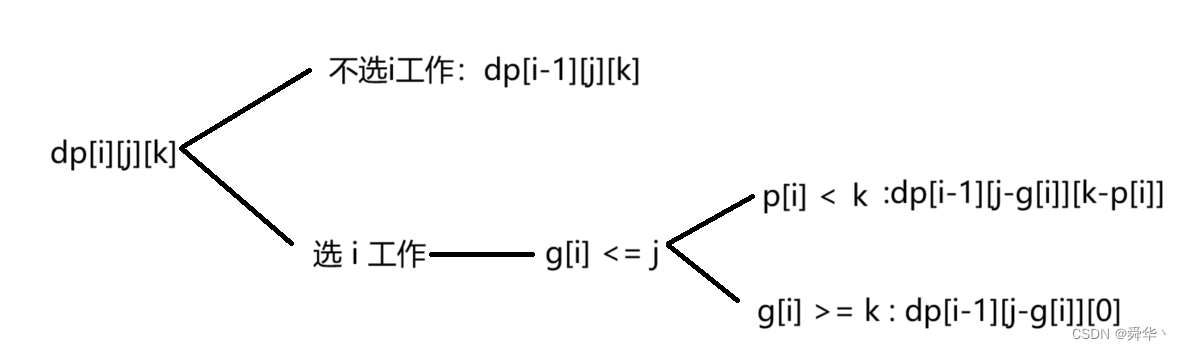
3. 初始化：0工作产生0利润，则不超过[0,j]员工，有一种选法，那就是不选。还有一点是下标映射关系需对应，此外不超过0名员工，与不超过0利润是合法的！因此j，k的起始位置都是从0开始的。
4. 填表顺序：从左到右
5. 返回值：dp[N][n][m]

class Solution {
public:int profitableSchemes(int n, int minProfit, vector<int>& group, vector<int>& profit) {const int MOD = 1e9 + 7;int N = group.size();int m = minProfit;vector<vector<vector<int>>> dp(N + 1,\vector<vector<int>>(n + 1,vector<int>(m + 1)));for(int j = 0; j <= n; j++)dp[0][j][0] = 1;for(int i = 1; i <= N; i++){for(int j = 0; j <= n; j++){for(int k = 0; k <= m; k++){dp[i][j][k] = dp[i-1][j][k];if(group[i-1] <= j)dp[i][j][k] += dp[i-1][j-group[i-1]][max(0,k-profit[i-1])];dp[i][j][k] %= MOD;}}}return dp[N][n][m]; }
};

九、似包非包问题

1. 组合总和 Ⅳ

• 链接:点击进入

1. 状态表示：dp[i] 表示总和为i的元素组合的个数。
2. 状态转移方程: 如果 nums[j] <= i, dp[i] += dp[i-nums[j]]
3. 初始化：为了保证后续的填表正确，dp[0]得初始化为1.
4. 填表顺序：从左往右
5. 返回值：dp[target]

class Solution {
public:int combinationSum4(vector<int>& nums, int target) {vector<double> dp(target + 1);dp[0] = 1;int n = nums.size();for(int i = 1; i <= target; i++){for(int j = 0; j < n; j++){if(nums[j] <= i){dp[i] += dp[i - nums[j]];}}}return dp[target];}
};

2. 不同的二叉搜索树

• 链接:不同的二叉搜索树
  

1. 状态表示：dp[i]表示1，i 结点的二叉搜索树的种数。
2. 状态转移方程:
   
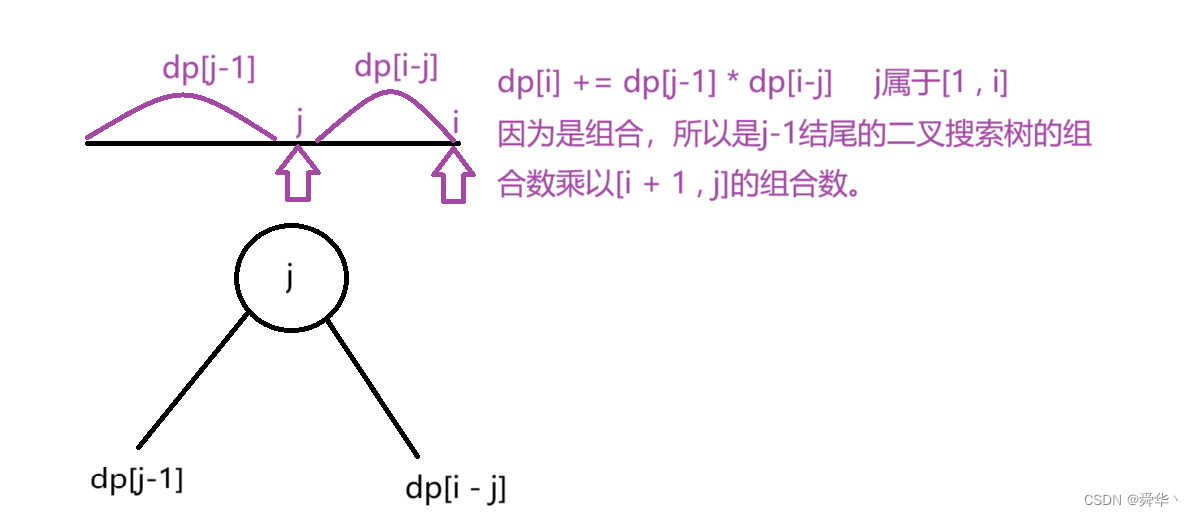
3. 初始化：为了保证后续的填表是正确的，这里dp[0]得初始化为1。
4. 填表顺序：从左往右
5. 返回值：dp[n]

class Solution {
public:int numTrees(int n) {vector<int> dp(n + 1);dp[0] = 1;for(int i = 1; i <= n; i++){for(int j = 1; j <= i; j++){dp[i] += dp[j-1] * dp[i-j];}}return dp[n];}
};

最后总结一下经验：

1. 一般来说是以一个位置为结尾，来分析状态转移方程的，除了第一个系列的最小花费爬楼梯和地下城游戏。
2. 分类讨论的思想在打家劫舍II与环形子数组的最大和中具有奇效。
3. 在暴力解决失败时，一般来说时间复杂度为N³ 且是二维的dp，这时就得再次分析状态转移方程，进行优化，一般来说都是哈希表进行的优化，因为dp毕竟是利用之前的信息，来更新现在的状态，所以优化一般都是查的过程，在最长定差子序列与最长等差数列中有所体现。
4. 状态转移方程博主见到的分为四类，一维的dp，一维的dp + 两个变量表示，二维的dp，三维的dp。
5. 技巧：一般如果状态比较比较多，这里可以化一个图进行表示状态之间的关系，这在买卖股票分析问题时有很大的帮助。
6. 难点：有的状态转移方程确实不好分析，比如正则表达式，盈利计划，主要是难在了细节，通常是初始化。还有一些问题会误认为是dp的完全背包问题，比如说第九系列的两道题，关键是要看到组合二字，才能排除完全背包问题。 最后有些问题是可以转换成背包问题，但是这个难就难在了转换方面，建议用列举法，仔细的观察规律。

尾序

 这是博主做了一遍之后，花了六天时间又做了一遍这些较为经典的题型，才总结的一篇三万字的博客，如果有所帮助，不妨点个赞鼓励一下博主！