文章目录
- 前言
- 什么是分冶
- 1.颜色分类
- 1.1 题目要求
- 1.2 做题思路
- 1.3 Java代码实现
- 2. 排序数组
- 2.1 题目要求
- 2.2 做题思路
- 2.3 Java代码实现
- 3.数组中的第k个最大元素
- 3.1 题目要求
- 3.2 做题思路
- 3.3 Java代码实现
- 4. 最小的k个数
- 4.1 题目要求
- 4.2 做题思路
- 4.3 Java代码实现
- 总结
前言
我相信看到这里很多人都学过八大排序了吧,其中快速排序是一种非常高效的排序方式,那么今天我们将会使用快速排序的算法来解决实际生活中的某些问题。
什么是分冶
分治算法是一种算法设计策略,它将大问题分解成更小的子问题,并通过解决子问题来解决原始问题。分治算法的基本思想是将问题分解成若干个规模较小但结构与原问题相似的子问题,然后递归地解决这些子问题,最后再将子问题的解合并得到原问题的解。
一般而言,分治算法可以分为三个步骤:
-
分解(Divide):将原问题划分成若干个规模较小且相互独立的子问题,通常通过递归方式实现。
-
解决(Conquer):递归地解决子问题。如果子问题的规模足够小,无需继续分解,直接求解并返回结果。
-
合并(Merge):将子问题的解合并成原问题的解。这一步骤通常涉及对子问题解的操作,以得到原问题的解。
分治算法的典型应用包括排序算法(如快速排序和归并排序)、查找算法(如二分查找)、图算法(如最大子数组和、最短路径问题)等。
分治算法的优点在于它能够高效地解决某些复杂问题,尤其适用于可以被划分为多个子问题的情况。通过将问题分解为更小的子问题,分治算法可以减少问题的规模,简化问题的解决过程。
然而,需要注意的是,并非所有问题都适合采用分治算法。在使用分治算法时,需要保证子问题相对独立且可以有效地解决。此外,分治算法在涉及大量递归调用时可能会带来额外的开销,因此在设计算法时需要注意递归深度与性能之间的平衡。
我们今天使用的快速排序的算法则是很好的利用了分冶将大事化小的思想来解决问题的,将整个数组分为若干小区间来进行排序,最终得到我们想要的结果。
1.颜色分类
https://leetcode.cn/problems/sort-colors/
1.1 题目要求
给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。
我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
必须在不使用库内置的 sort 函数的情况下解决这个问题。
示例 1:
输入:nums = [2,0,2,1,1,0]
输出:[0,0,1,1,2,2]
示例 2:
输入:nums = [2,0,1]
输出:[0,1,2]
提示:
- n == nums.length
- 1 <= n <= 300
- nums[i] 为 0、1 或 2
进阶:
你能想出一个仅使用常数空间的一趟扫描算法吗?
class Solution {public void sortColors(int[] nums) {}
}
1.2 做题思路
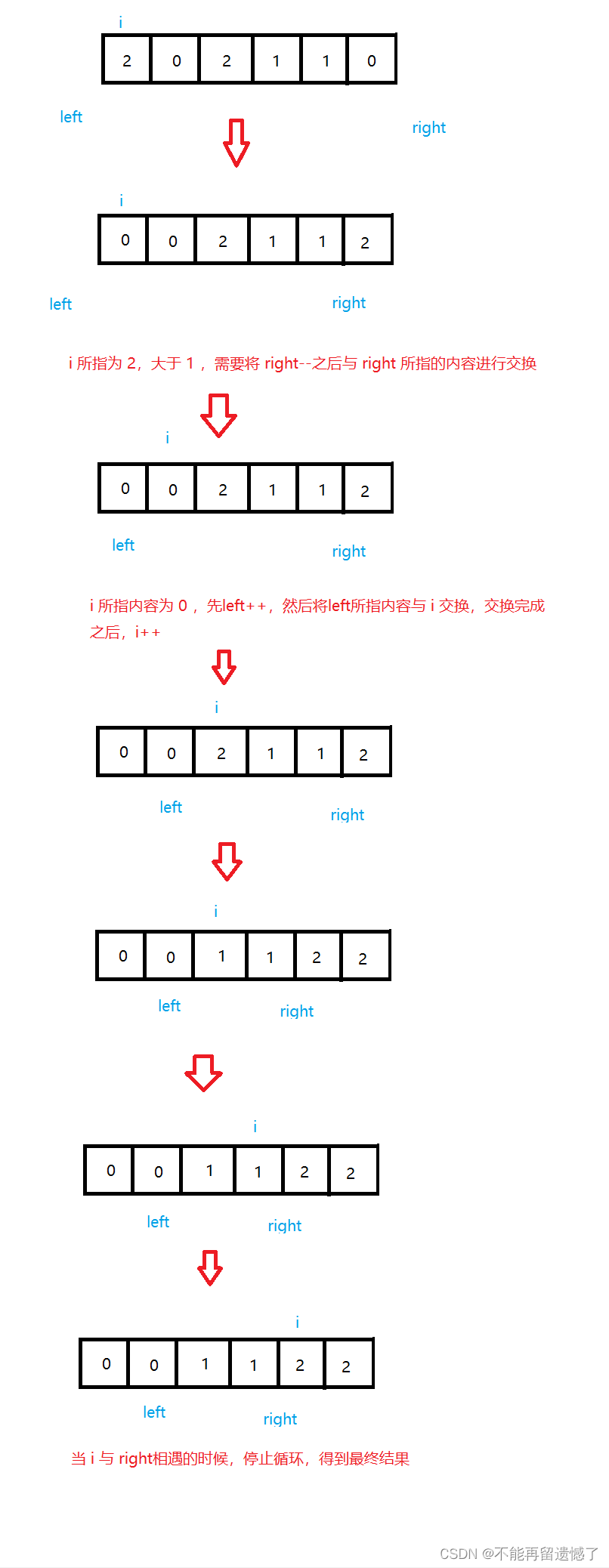
前面学习的快速排序,每一趟排序过程会以一个数为基准,使最终结果这个基准值的左边小于等于这个基准值,右边部分都是大于这个基准值,所以这个题目我们同样可以使用这种快排的思想,以1为基准,然后用 i 来遍历数组,left 指针以及 left 指针左边都是0,right 指针以及 right 指针右边部分都是2。left 一开始的位置指向 -1,right 指针指向 n(数组大小),当 i 所指向的数据小于 1 的时候,就先将 left++ ,然后将left 所指的内容与 i 所指的内容交换位置,交换结束之后,i++;如果 i 所指向的内容等于 1 的之后,直接i++;如果 i 指向的内容大于 1 ,则先需要将 right–,然后交换right 与 i 所指向的内容,但是这里交换完成之后,i 不能++,因为与 right 指向的内容交换位置之后,i 所指向的内容是 i 没有遍历过的,如果 i++,那么这个数字将会被跳过。
1.3 Java代码实现
class Solution {private void swap(int[] nums, int i, int j) {int t = nums[i];nums[i] = nums[j];nums[j] = t;}public void sortColors(int[] nums) {int n = nums.length;int left = -1,right = n,i = 0;while(i < right) {if(nums[i] < 1) swap(nums,++left,i++);else if(nums[i] == 1) i++;else swap(nums,--right,i);}}
}
2. 排序数组
https://leetcode.cn/problems/sort-an-array/
2.1 题目要求
给你一个整数数组 nums,请你将该数组升序排列。
示例 1:
输入:nums = [5,2,3,1]
输出:[1,2,3,5]
示例 2:
输入:nums = [5,1,1,2,0,0]
输出:[0,0,1,1,2,5]
提示:
- 1 <= nums.length <= 5 * 104
- -5 * 104 <= nums[i] <= 5 * 104
class Solution {public int[] sortArray(int[] nums) {}
}
2.2 做题思路
这道题就很简单明了,直接将数组进行升序排序,我们可以使用分冶的思想,讲整个数组分为 n 个部分,然后在这 n 个小部分中使用快排的思想进行排序,需要注意的是,如果数组趋于有序的话,快速排序的时间复杂度会下降到 O(N^2) ,所以我们可以对快速排序进行优化,优化的方式有很多:三数取中等等,这里我们使用的方式是随机取基准值的方法吗,这样能使快排的时间复杂度基本趋于 O(N*logN)。
2.3 Java代码实现
class Solution {public int[] sortArray(int[] nums) {qsort(nums,0,nums.length-1);return nums;}private void qsort(int[] nums, int l, int r) {if(l >= r) return; //递归结束的条件int left = l-1,right = r + 1, i = l;//在[l,r]区间内,随机取一个数作为基准值int key = nums[new Random().nextInt(r - l + 1) + l];while(i < right) {if(nums[i] < key) swap(nums,++left,i++);else if(nums[i] == key) i++;else swap(nums,--right,i);}//当将基准值排序到最终位置之后,还需要将基准位置左右两边部分继续排序qsort(nums,l,left);qsort(nums,right,r);}private void swap(int[] nums, int i, int j) {int t = nums[i];nums[i] = nums[j];nums[j] = t;}
}
3.数组中的第k个最大元素
https://leetcode.cn/problems/kth-largest-element-in-an-array/
3.1 题目要求
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例 1:
输入: [3,2,1,5,6,4], k = 2
输出: 5
示例 2:
输入: [3,2,3,1,2,4,5,5,6], k = 4
输出: 4
提示:
- 1 <= k <= nums.length <= 105
- -104 <= nums[i] <= 104
class Solution {public int findKthLargest(int[] nums, int k) {}
}
3.2 做题思路
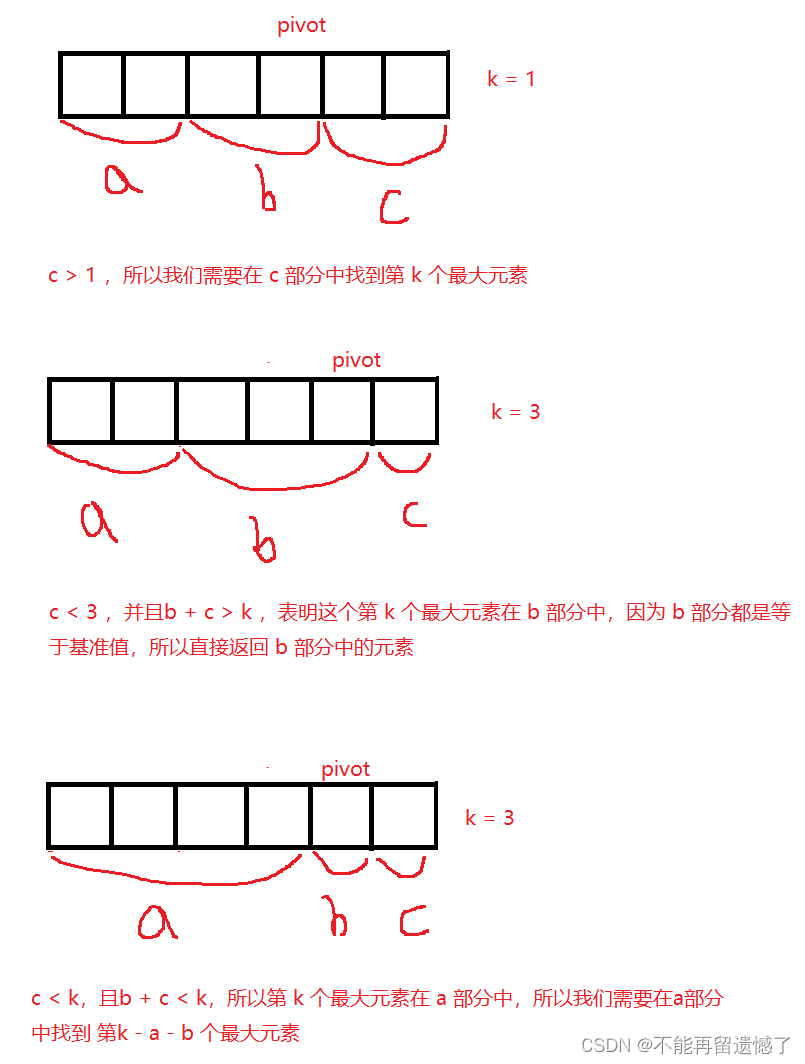
要想找到数组中的第k个最大元素,我们能想到的还是将数组进行排序,然后从大到小找到第k个元素。这道题目可以使用堆排序,创建出大小为 k 的小根堆。但是我们不使用堆排序的方法,而是使用分冶-快排的方法来解决。如何使用快排的方式来解决呢?同样是先找一个元素作为基准值,进行快排,将数组分为 a——小于基准值的部分、b——等于基准值的部分和c——大于基准值的部分,因为要找到第 k 个最大的元素,所以首先我们需要在大于基准的部分中找这个元素是否存在,如果 c 部分的长度大于等于 k ,则说明这个部分中存在第 k 大的元素,然后我们在这个部分中继续寻找;如果 c 的长度小于 k ,并且 b + c 的长度大于等于 k,那么我们可以直接返回 b 部分的元素,因为 c 部分的长度小于 k ,所以这个第 k 大的元素存在于 b 部分,而 b 部分都是等于基准值的部分,可以直接返回;如果前面两种情况都不存在,那么这个第 k 大的元素就在 a 部分,我们需要在 a 部分中找到第 k - b - c 大的元素,这个操作跟前面的递归操作类似。
3.3 Java代码实现
class Solution {public int findKthLargest(int[] nums, int k) {return qsort(nums,0,nums.length-1,k);}private int qsort(int[] nums, int l, int r, int k) {int key = nums[new Random().nextInt(r - l + 1) + l];int left = l-1, right = r + 1, i = l;while(i < right) {if(nums[i] < key) swap(nums,++left,i++);else if(nums[i] == key) i++;else swap(nums,--right,i);}//c表示大于key的部分,b表示等于key的部分,剩下的部分就是小于key的部分int c = r - right + 1;int b = right - left - 1;if(c >= k) return qsort(nums,right,r,k);else if(b + c >= k) return key;else return qsort(nums,l,left,k - b - c);}private void swap(int[] nums, int i, int j) {int tmp = nums[i];nums[i] = nums[j];nums[j] = tmp;}
}
4. 最小的k个数
https://leetcode.cn/problems/zui-xiao-de-kge-shu-lcof/
4.1 题目要求
输入整数数组 arr ,找出其中最小的 k 个数。例如,输入4、5、1、6、2、7、3、8这8个数字,则最小的4个数字是1、2、3、4。
示例 1:
输入:arr = [3,2,1], k = 2
输出:[1,2] 或者 [2,1]
示例 2:
输入:arr = [0,1,2,1], k = 1
输出:[0]
限制:
- 0 <= k <= arr.length <= 10000
- 0 <= arr[i] <= 10000
class Solution {public int[] getLeastNumbers(int[] arr, int k) {}
}
4.2 做题思路
因为这道题目没有要求要按照元素的大小顺序返回,所以我们可以模仿上面的第 k 个最大元素的思路进行分冶-快排的算法,对数组进行简单的排序,并且将数组分为:a——小于基准值的部分,b——等于基准值的部分,c——大于基准值的部分。
如果a > k,则需要在 a 部分中继续递归,找到最小的 k 个数;如果a <= k,但是 a + b >= k ,因为 b 部分都是相等的数据,所以可以直接返回;如果前面两种情况都不符合的话,就还需要在 c 部分中继续进行排序,直到在 c 部分中找到 第k - a -b小的元素,然后该位置之前的部分就是我们需要的最小的 k 个数。
4.3 Java代码实现
class Solution {public int[] getLeastNumbers(int[] nums, int k) {qsort(nums,0,nums.length-1,k);int[] ret = new int[k];for(int i = 0; i < k; i++) ret[i] = nums[i];return ret;}private void qsort(int[] nums, int l, int r, int k) {int key = nums[new Random().nextInt(r - l + 1) + l];int left = l - 1, right = r + 1,i = l;while(i < right) {if(nums[i] < key) swap(nums,++left,i++);else if(nums[i] == key) i++;else swap(nums,--right,i);}int a = left - l + 1,b = right - left - 1;if(a > k) qsort(nums,l,left,k);else if(a + b >= k) return;else qsort(nums,right,r,k - a - b);}private void swap(int[] nums, int i, int j) {int t = nums[i];nums[i] = nums[j];nums[j] = t;}
}
总结
通过本篇博客,我们深入了解了分治算法以及其在快速排序算法中的应用。快速排序是一种高效的排序算法,它利用了分治策略,将大问题逐步分解为规模较小的子问题,并通过递归地解决和合并子问题来完成整个排序过程。
快速排序算法的核心思想是选择一个基准元素,将待排序数组分割成两个子数组,一个小于等于基准的子数组和一个大于基准的子数组。然后,递归地对两个子数组进行排序,最后合并得到最终的有序数组。
快速排序算法具有以下优点:
-
高效性:快速排序算法的平均时间复杂度为O(nlogn),在实际应用中表现出良好的性能。它通过不断地将数组划分为较小的子数组进行排序,从而减少了比较和交换的次数。
-
原地排序:快速排序算法可以在原数组上进行排序,不需要额外的辅助空间。这对于内存受限的环境来说具有重要意义。
然而,快速排序算法也存在一些注意事项和局限性:
-
对于初始数组的选择敏感:快速排序算法的性能高度依赖于选择的基准元素。最理想的情况是选择一个能够将数组划分成大小相似的子数组的基准元素,以避免出现最坏情况的时间复杂度。
-
递归深度:在快速排序算法中,递归调用的深度取决于划分操作的方式和基准元素的选择。当数组中存在大量重复元素时,可能会导致递归深度增加,影响算法的性能。
总结而言,快速排序算法是一种高效、原地排序的算法,通过分治策略实现了对待排序数组的快速排序。它在实践中被广泛使用,具有较好的性能。然而,需要根据具体问题选择合适的基准元素,并考虑递归深度对算法性能的影响。