1、题目：

给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。
请你 合并 nums2 到 nums1 中，使合并后的数组同样按 非递减顺序 排列。

• 注意：最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。

2、分析特点：

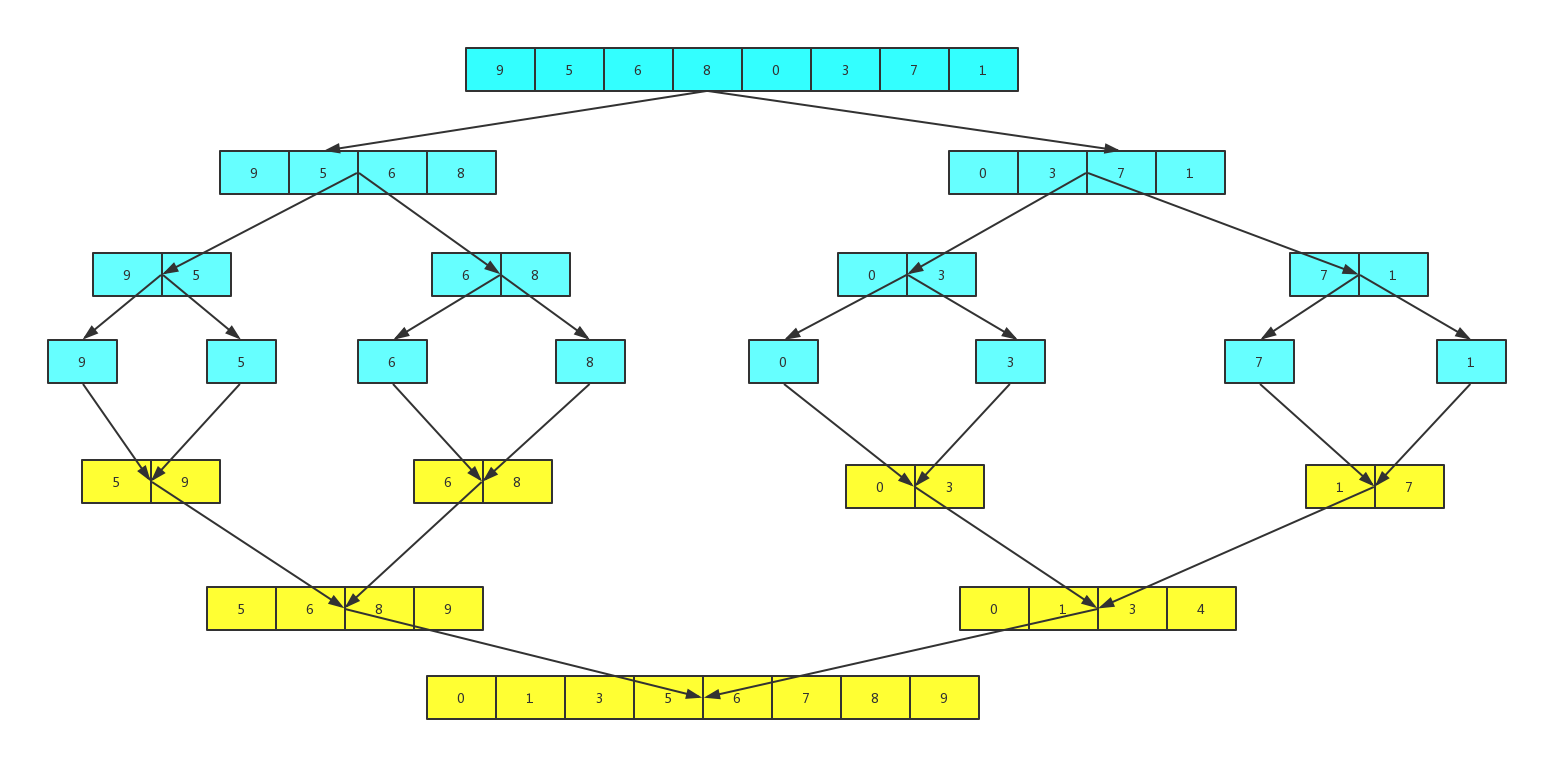
两个数组已经被排序 ，相当于两条有序的队列，非递减，从小到大排队，每次都从两条队伍中取走最小的那个数放到结果中。

3、代码：

   public void merge(int[] nums1, int m, int[] nums2, int n) {int p1 = 0, p2 = 0;int[] sorted = new int[m + n];int cur;while (p1 < m || p2 < n) {if (p1 == m) {cur = nums2[p2++];} else if (p2 == n) {cur = nums1[p1++];} else if (nums1[p1] < nums2[p2]) {cur = nums1[p1++];} else {cur = nums2[p2++];}sorted[p1 + p2 - 1] = cur;}for (int i = 0; i != m + n; ++i) {nums1[i] = sorted[i];}}

4、复杂度分析：

• 时间复杂度：O(m+n)O(m+n)O(m+n)。 指针移动单调递增，最多移动 m+nm+nm+n 次，因此时间复杂度为 O(m+n)O(m+n)O(m+n)。

• 空间复杂度：O(m+n)O(m+n)O(m+n)。 需要建立长度为 m+nm+nm+n 的中间数组 sorted。

5、总结：

本题比较简单，只需要抓住，有序递增的两个数组，直接当队列，抓最小。当然更简单的是直接把其中一个数组的全部元素存储到另外一个数组后面的空间，然后利用封装好的方法排序即可，即 Arrays.sort() 方法

如果本文对你有帮助的话记得给一乐点个赞哦，感谢！