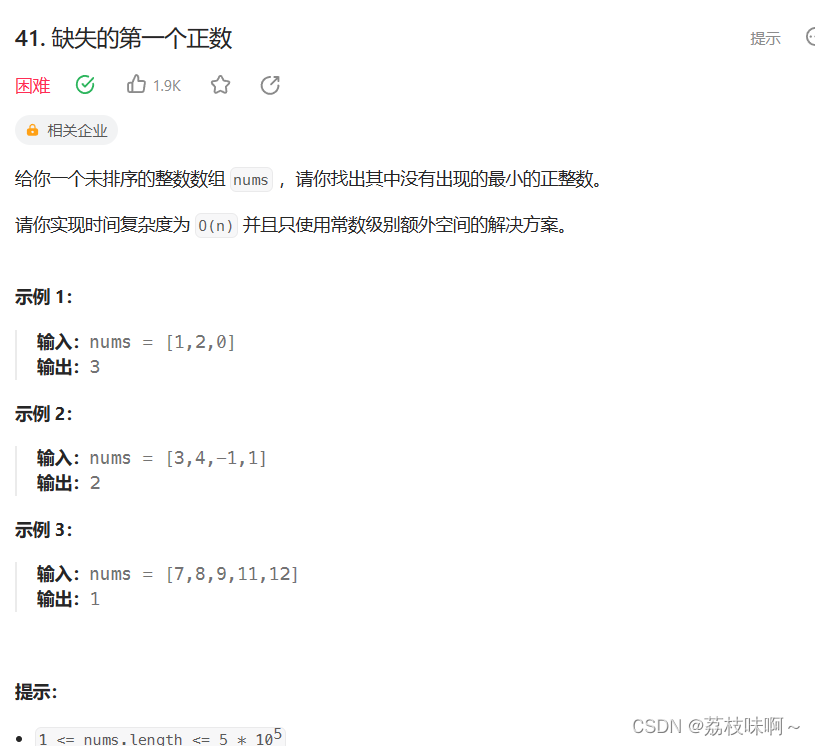
看到题目难度是hard的时候我就想先写半个小时试试看,如果没思路就看题解,没想到我就写了10来分钟就给通过了,通过的时候我都不敢相信,我感觉我是走了后门的,因为我用了 Arrays.sort()方法,他的时间复杂度是O(nlogn)已经超过n了,而且我的算法很垃圾。
我先把用Arrays.sort()把数组排序,然后从头遍历数组,先把负数和0直接跳过,然后先把ans初始化为1,如果num[i]==ans就可以判断下一个了看nums[i+1]是不是等于ans++,如果num[i]!=ans就直接把ans返回就行,但是后面提交遇到了一种状况就是有很多个相同的数比如1 1 1 2 2这样,于是我加了一行,就是如果nums[i]==ans-1,就是还和上一个数相同的话就直接跳过,居然AC了,hard不可能这么简单,应该是我走了后门。
class Solution {public int firstMissingPositive(int[] nums) {Arrays.sort(nums);int ans=1;int n = nums.length;for(int i=0;i<n;i++){if(nums[i]<=0 || nums[i]==ans-1)continue;if(nums[i] != ans){return ans;}else{ans++;}}return ans;}
}看看题解的正规解法,题解是真的非常的巧妙。
对于一个长度为N的数组,未出现的最小正数只能出现在[N, N+1]中,因为如果[1,N]都出现了答案就是N+1,否则是[1, N]中未出现的最小正数,于是我们可以去遍历数组,对于遍历到的数x,如果x属于[1,N]就把数组第x-1个位置打上标记,如果数组中所有数都打上了标记,那么未出现的最小正数就是N+1,否者是最小的没标记的数。
如何设计这个标记呢?我们可以先把小于等于0的数变成N+1,这样就可以不考虑这些负数了,然后去遍历数组中的每一个数x(这个数可能会被前面的数修改成了负数,所以我们取绝对值|x|),如果他属于[1,N]那就把 下标为|x-1|的数改为负数,这样就完成了标记,最后返回数组中第一个正数的下标+1,如果都是负数就返回N+1。很巧妙,但是鬼想得到。
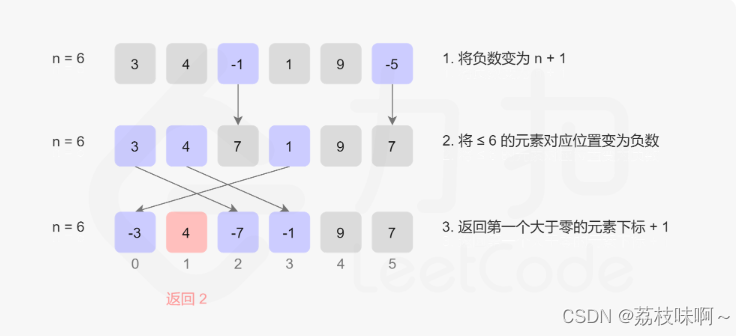
以下是题解代码:
class Solution {public int firstMissingPositive(int[] nums) {int n = nums.length;for (int i = 0; i < n; ++i) {if (nums[i] <= 0) {nums[i] = n + 1;}}for (int i = 0; i < n; ++i) {int num = Math.abs(nums[i]);if (num <= n) {nums[num - 1] = -Math.abs(nums[num - 1]);}}for (int i = 0; i < n; ++i) {if (nums[i] > 0) {return i + 1;}}return n + 1;}
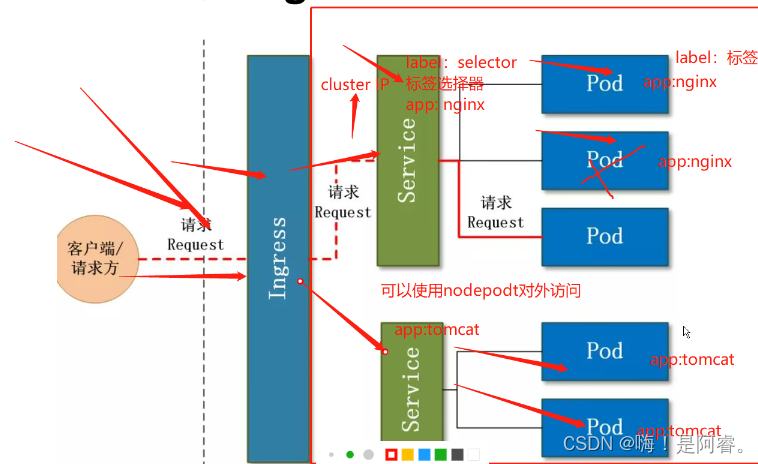
}


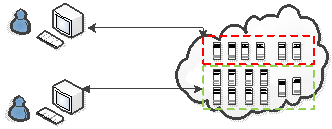

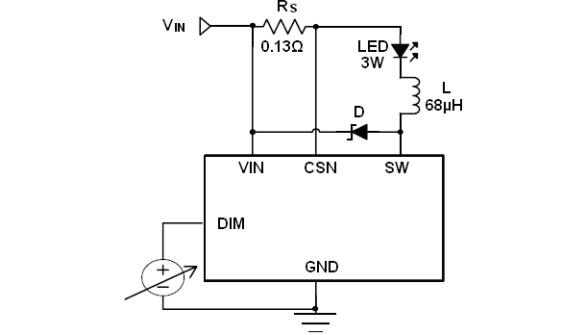
![【mybatis-plus】多数据源切换[dynamic-datasource] 手动切换数据源](https://img-blog.csdnimg.cn/e66182f54a0346e69b68a25c42600eaa.png)
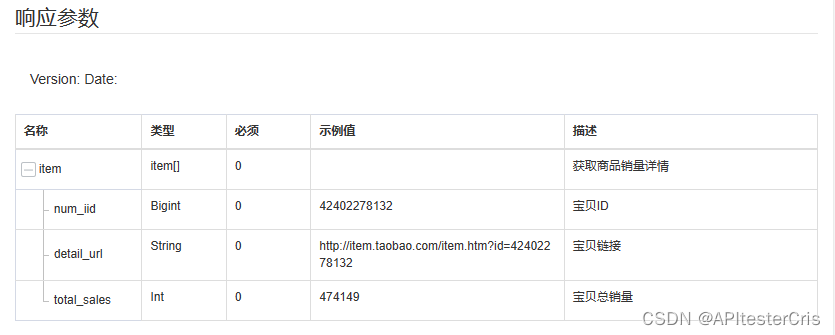
![[羊城杯 2023] web](https://img-blog.csdnimg.cn/fe2d2bcdeac545f7914bbc1703e68ae2.png)