代码随想录笔记--二叉树篇

目录

1--递归遍历

1-1--前序遍历

1-2--中序遍历

1-3--后序遍历

2--迭代遍历

2-1--前序遍历

2-2--后序遍历

2-3--中序遍历

3--二叉树的层序遍历

4--翻转二叉树

5--对称二叉树

6--二叉树最大深度

7--二叉树的最小深度

8--完全二叉树节点的数量

9--平衡二叉树

10--二叉树的所有路径

11--左叶子之和

12--找树左下角的值

13--路径总和

14--从中序与后序遍历序列构造二叉树

15--最大二叉树

16--合并二叉树

17--二叉搜索树中的搜索

18--验证二叉搜索树

19--二叉搜索树的最小绝对差

20--二叉搜索树中的众数

21--二叉树的最近公共祖先

22--二叉搜索树的最近公共祖先

23--二叉搜索树中的插入操作

24--删除二叉搜索树中的节点

25--修建二叉搜索树

26--将有序数组转换为二叉搜索树

27--把二叉搜索树转换为累加树

1--递归遍历

1-1--前序遍历

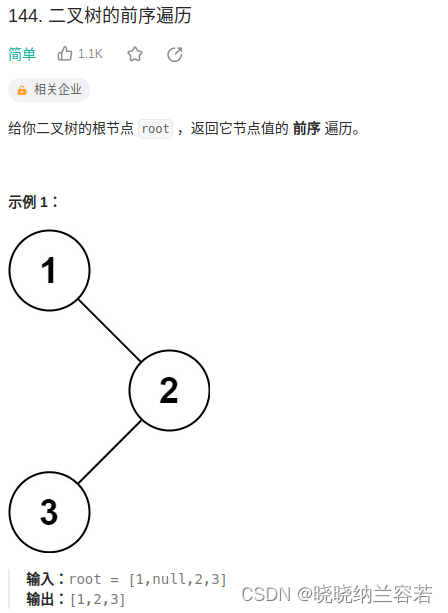
前序遍历：根→左→右；

#include <iostream>
#include <vector>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution{
public:std::vector<int> preorderTraversal(TreeNode* root) {std::vector<int> res;dfs(root, res);return res;}void dfs(TreeNode* root, std::vector<int>& res){if(root == nullptr) return;res.push_back(root->val);dfs(root->left, res);dfs(root->right, res);}
};int main(int argc, char* argv[]){// root = [1, null, 2, 3]TreeNode *Node1 = new TreeNode(1);TreeNode *Node2 = new TreeNode(2);TreeNode *Node3 = new TreeNode(3);Node1->right = Node2;Node2->left = Node3;Solution S1;std::vector<int> res = S1.preorderTraversal(Node1);for(auto item : res) std::cout << item << " ";std::cout << std::endl;return 0;
}

1-2--中序遍历

中序遍历：左→根→右；

#include <iostream>
#include <vector>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution{
public:std::vector<int> inorderTraversal(TreeNode* root) {std::vector<int> res;dfs(root, res);return res;}void dfs(TreeNode* root, std::vector<int>& res){if(root == nullptr) return;dfs(root->left, res);res.push_back(root->val);dfs(root->right, res);}
};int main(int argc, char* argv[]){// root = [1, null, 2, 3]TreeNode *Node1 = new TreeNode(1);TreeNode *Node2 = new TreeNode(2);TreeNode *Node3 = new TreeNode(3);Node1->right = Node2;Node2->left = Node3;Solution S1;std::vector<int> res = S1.inorderTraversal(Node1);for(auto item : res) std::cout << item << " ";std::cout << std::endl;return 0;
}

1-3--后序遍历

后序遍历：左→右→根；

#include <iostream>
#include <vector>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution{
public:std::vector<int> postorderTraversal(TreeNode* root) {std::vector<int> res;dfs(root, res);return res;}void dfs(TreeNode* root, std::vector<int>& res){if(root == nullptr) return;dfs(root->left, res);dfs(root->right, res);res.push_back(root->val);}
};int main(int argc, char* argv[]){// root = [1, null, 2, 3]TreeNode *Node1 = new TreeNode(1);TreeNode *Node2 = new TreeNode(2);TreeNode *Node3 = new TreeNode(3);Node1->right = Node2;Node2->left = Node3;Solution S1;std::vector<int> res = S1.postorderTraversal(Node1);for(auto item : res) std::cout << item << " ";std::cout << std::endl;return 0;
}

2--迭代遍历

2-1--前序遍历

        基于栈结构，先将根节点入栈，再将节点从栈中弹出，如果节点的右孩子不为空，则右孩子入栈；如果节点的左孩子不为空，则左孩子入栈；

        循环出栈处理节点，并将右孩子和左孩子存在栈中（右孩子先进栈，左孩子再进栈，因为栈先进后出，这样可以确保左孩子先出栈，符合根→左→右的顺序）；

#include <iostream>
#include <vector>
#include <stack>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution{
public:std::vector<int> preorderTraversal(TreeNode* root) {std::vector<int> res;if(root == nullptr) return res;std::stack<TreeNode*> stk;stk.push(root);while(!stk.empty()){TreeNode *tmp = stk.top();stk.pop();res.push_back(tmp->val);if(tmp->right != nullptr) stk.push(tmp->right); // 右if(tmp->left != nullptr) stk.push(tmp->left); // 左}return res;}
};int main(int argc, char* argv[]){// root = [1, null, 2, 3]TreeNode *Node1 = new TreeNode(1);TreeNode *Node2 = new TreeNode(2);TreeNode *Node3 = new TreeNode(3);Node1->right = Node2;Node2->left = Node3;Solution S1;std::vector<int> res = S1.preorderTraversal(Node1);for(auto item : res) std::cout << item << " ";std::cout << std::endl;return 0;
}

2-2--后序遍历

        可以使用两个栈来实现，一个是遍历栈，一个是收集栈，参考之前的笔记：后序遍历的迭代实现        

        也可以类似于前序遍历，基于一个栈实现，只不过需要改变入栈顺序：每出栈处理一个节点，其左孩子入栈，再右孩子入栈；此时处理顺序为：根->右->左，最后将结果 reverse 即可；

#include <iostream>
#include <vector>
#include <stack>
#include <algorithm>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution{
public:std::vector<int> postorderTraversal(TreeNode* root) {std::vector<int> res;if(root == nullptr) return res;std::stack<TreeNode*> stk;stk.push(root);while(!stk.empty()){TreeNode* tmp = stk.top();stk.pop();if(tmp->left != nullptr) stk.push(tmp->left);if(tmp->right != nullptr) stk.push(tmp->right);res.push_back(tmp->val);}// 反转std::reverse(res.begin(), res.end());return res;}
};int main(int argc, char* argv[]){// root = [1, null, 2, 3]TreeNode *Node1 = new TreeNode(1);TreeNode *Node2 = new TreeNode(2);TreeNode *Node3 = new TreeNode(3);Node1->right = Node2;Node2->left = Node3;Solution S1;std::vector<int> res = S1.postorderTraversal(Node1);for(auto item : res) std::cout << item << " ";std::cout << std::endl;return 0;
}

2-3--中序遍历

基于栈结构，初始化一个栈，根节点入栈；

        ①：左子结点全部入栈；

        ②：结点出栈，处理结点；

        ③：对出栈结点的右子树重复执行第 ① 步操作；

#include <iostream>
#include <vector>
#include <stack>
#include <algorithm>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution{
public:std::vector<int> inorderTraversal(TreeNode* root) {std::vector<int> res;if(root == nullptr) return res;std::stack<TreeNode*> stk;while(!stk.empty() || root != nullptr){if(root != nullptr){ // 左子结点全部入栈stk.push(root);root = root->left;}else{TreeNode *tmp = stk.top();stk.pop();res.push_back(tmp->val);// 出栈节点的右孩子执行相同操作root = tmp->right;}    }return res;}
};int main(int argc, char* argv[]){// root = [1, null, 2, 3]TreeNode *Node1 = new TreeNode(1);TreeNode *Node2 = new TreeNode(2);TreeNode *Node3 = new TreeNode(3);Node1->right = Node2;Node2->left = Node3;Solution S1;std::vector<int> res = S1.inorderTraversal(Node1);for(auto item : res) std::cout << item << " ";std::cout << std::endl;return 0;
}

3--二叉树的层序遍历

主要思路：

        经典广度优先搜索，基于队列；

        对于本题需要将同一层的节点放在一个数组中，因此遍历的时候需要用一个变量 nums 来记录当前层的节点数，即 nums 等于队列元素的数目；

#include <iostream>
#include <vector>
#include <queue>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:std::vector<std::vector<int>> levelOrder(TreeNode* root) {std::vector<std::vector<int>> res;if(root == nullptr) return res;std::queue<TreeNode*> q;q.push(root);while(!q.empty()){int nums = q.size(); // 当前层的节点数std::vector<int> tmp;while(nums > 0){ // 遍历处理同一层TreeNode *cur = q.front();q.pop();tmp.push_back(cur->val);if(cur->left != nullptr) q.push(cur->left);if(cur->right != nullptr) q.push(cur->right);nums--;}res.push_back(tmp); // 记录当前层的元素}return res;}
};int main(int argc, char* argv[]){// root = [1, null, 2, 3]TreeNode *Node1 = new TreeNode(3);TreeNode *Node2 = new TreeNode(9);TreeNode *Node3 = new TreeNode(20);TreeNode *Node4 = new TreeNode(15);TreeNode *Node5 = new TreeNode(7);Node1->left = Node2;Node1->right = Node3;Node3->left = Node4;Node3->right = Node5;Solution S1;std::vector<std::vector<int>> res = S1.levelOrder(Node1);for(auto item : res) {for (int v : item) std::cout << v << " ";std::cout << std::endl;}return 0;
}

4--翻转二叉树

主要思路：

        递归交换左右子树；

#include <iostream>
#include <vector>
#include <queue>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:TreeNode* invertTree(TreeNode* root) {reverse(root);return root;}void reverse(TreeNode *root){if(root == nullptr) return;reverse(root->left);reverse(root->right);TreeNode *tmp = root->left;root->left = root->right;root->right = tmp;}
};// 层次遍历打印
void PrintTree(TreeNode *root){std::queue<TreeNode*> q;q.push(root);while(!q.empty()) {TreeNode *tmp = q.front();q.pop();std::cout << tmp->val << " ";if(tmp->left != nullptr) q.push(tmp->left);if(tmp->right != nullptr) q.push(tmp->right);}
}int main(int argc, char* argv[]){// root = [4,2,7,1,3,6,9]TreeNode *Node1 = new TreeNode(4);TreeNode *Node2 = new TreeNode(2);TreeNode *Node3 = new TreeNode(7);TreeNode *Node4 = new TreeNode(1);TreeNode *Node5 = new TreeNode(3);TreeNode *Node6 = new TreeNode(6);TreeNode *Node7 = new TreeNode(9);Node1->left = Node2;Node1->right = Node3;Node2->left = Node4;Node2->right = Node5;Node3->left = Node6;Node3->right = Node7;Solution S1;TreeNode *res = S1.invertTree(Node1);PrintTree(res);
}

5--对称二叉树

主要思路：

        递归判断左树的左子树是否与右数的右子树相等，左树的右子树是否与右树的左子树相等；

#include <iostream>
#include <vector>
#include <queue>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:bool isSymmetric(TreeNode* root) {if(root == nullptr) return true;bool res = dfs(root->left, root->right);return res;}bool dfs(TreeNode *left, TreeNode *right){if((left != nullptr && right == nullptr) ||(left == nullptr && right != nullptr)) return false;if(left == nullptr && right == nullptr) return true;if (left->val != right->val) return false;bool isSame1 = dfs(left->left, right->right);bool isSame2 = dfs(left->right, right->left);return isSame1 && isSame2;}
};int main(int argc, char* argv[]){// root = [4,2,7,1,3,6,9]TreeNode *Node1 = new TreeNode(1);TreeNode *Node2 = new TreeNode(2);TreeNode *Node3 = new TreeNode(2);TreeNode *Node4 = new TreeNode(3);TreeNode *Node5 = new TreeNode(4);TreeNode *Node6 = new TreeNode(4);TreeNode *Node7 = new TreeNode(3);Node1->left = Node2;Node1->right = Node3;Node2->left = Node4;Node2->right = Node5;Node3->left = Node6;Node3->right = Node7;Solution S1;bool res = S1.isSymmetric(Node1);if(res) std::cout << "true" << std::endl;else std::cout << "false" << std::endl;
}

6--二叉树最大深度

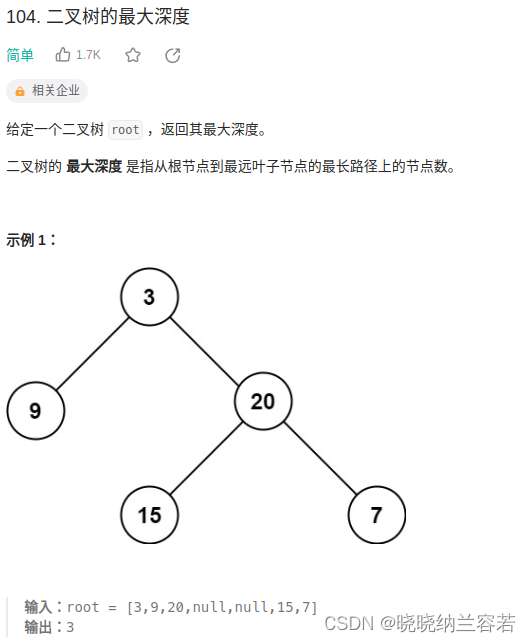
主要思路：

        递归计算左右子树的深度，选取两者最大值 +1 返回；

#include <iostream>
#include <vector>
#include <queue>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:int maxDepth(TreeNode* root) {if(root == nullptr) return 0;int res = dfs(root);return res;}int dfs(TreeNode* root){if(root == nullptr) return 0;int left_height = dfs(root->left);int right_height = dfs(root->right);int cur_height = std::max(left_height, right_height) + 1;return cur_height;}
};int main(int argc, char* argv[]){// root = [3,9,20,null,null,15,7]TreeNode *Node1 = new TreeNode(3);TreeNode *Node2 = new TreeNode(9);TreeNode *Node3 = new TreeNode(20);TreeNode *Node4 = new TreeNode(15);TreeNode *Node5 = new TreeNode(7);Node1->left = Node2;Node1->right = Node3;Node3->left = Node4;Node3->right = Node5;Solution S1;int res = S1.maxDepth(Node1);std::cout << res << std::endl;return 0;
}

7--二叉树的最小深度

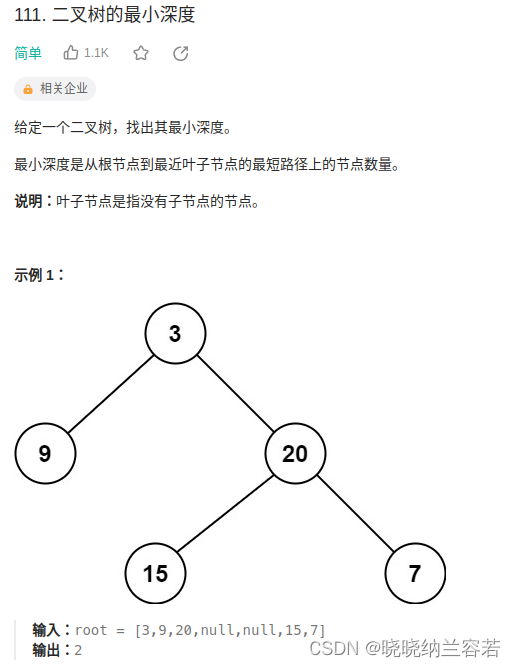
主要思路：

        与上题有点类似，递归返回最小深度即可，但需要剔除根节点一个子树为空的情况；

        对于一个根节点，其中一个子树为空，则其最小深度是不为空的子树的深度；

#include <iostream>
#include <vector>
#include <queue>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:int minDepth(TreeNode* root) {if(root == nullptr) return 0;return dfs(root);}int dfs(TreeNode *root){if(root == nullptr) return 0;// 剔除两种情况if(root->left == nullptr) return dfs(root->right) + 1;else if(root->right == nullptr) return dfs(root->left) + 1;else{int left_height = dfs(root->left);int right_height = dfs(root->right);int cur_min_height = std::min(left_height, right_height) + 1;return cur_min_height;}}
};int main(int argc, char* argv[]){// root = [3,9,20,null,null,15,7]TreeNode *Node1 = new TreeNode(3);TreeNode *Node2 = new TreeNode(9);TreeNode *Node3 = new TreeNode(20);TreeNode *Node4 = new TreeNode(15);TreeNode *Node5 = new TreeNode(7);Node1->left = Node2;Node1->right = Node3;Node3->left = Node4;Node3->right = Node5;Solution S1;int res = S1.minDepth(Node1);std::cout << res << std::endl;return 0;
}

8--完全二叉树节点的数量

主要思路：

        普通二叉树可以通过层次遍历来统计节点数目；

        对于本题中的完全二叉树，可以通过 2**k - 1 的公式来计算二叉树节点的数目；

        首先需判断一个子树是否为完全二叉树，如果是则通过上式计算；如果不是完全二叉树，则对于当前子树，需要分别向左右子树递归计算其节点数目（相当于获取信息），最后将结果相加（相当于处理信息），并加上1返回即可；

#include <iostream>
#include <vector>
#include <queue>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:int countNodes(TreeNode* root) {if(root == nullptr) return 0;return dfs(root);}int dfs(TreeNode *root){if(root == nullptr) return 0;TreeNode *left = root->left, *right = root->right;int left_height = 0, right_height = 0;while(left != nullptr){left = left->left;left_height++;}while(right != nullptr){right = right->right;right_height++;}if(left_height == right_height) return (2<<left_height) - 1; // 满二叉树int left_nums = dfs(root->left);int right_nums = dfs(root->right);return left_nums + right_nums + 1;}
};int main(int argc, char* argv[]){// root = [1,2,3,4,5,6]TreeNode *Node1 = new TreeNode(1);TreeNode *Node2 = new TreeNode(2);TreeNode *Node3 = new TreeNode(3);TreeNode *Node4 = new TreeNode(4);TreeNode *Node5 = new TreeNode(5);TreeNode *Node6 = new TreeNode(6);Node1->left = Node2;Node1->right = Node3;Node2->left = Node4;Node2->right = Node5;Node3->left = Node6;Solution S1;int res = S1.countNodes(Node1);std::cout << res << std::endl;return 0;
}

9--平衡二叉树

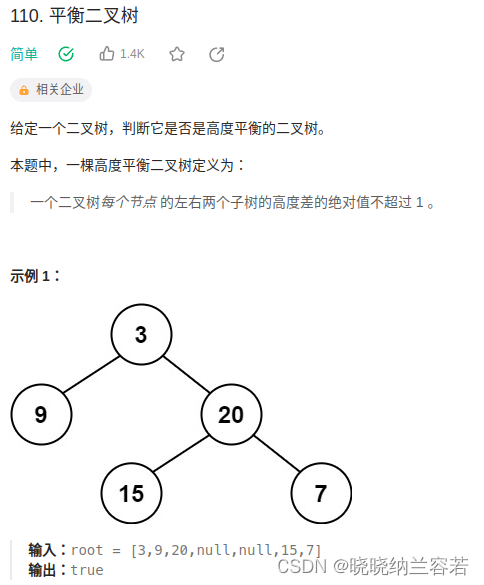
主要思路：

        通过高度差不大于1，来递归判断子树是否是平衡二叉树，不是则返回-1，是则返回对应的高度；

#include <iostream>
#include <vector>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:bool isBalanced(TreeNode* root) {if(root == nullptr) return true;int height = dfs(root);return height == -1 ? false : true;}int dfs(TreeNode *root){if(root == nullptr) return 0;int left_height = dfs(root->left);if(left_height == -1) return -1;int right_height = dfs(root->right);if(right_height == -1) return -1;if(std::abs(left_height - right_height) > 1) return -1;else return std::max(left_height, right_height) + 1;}
};int main(int argc, char* argv[]){// root = [3,9,20,null,null,15,7]TreeNode *Node1 = new TreeNode(3);TreeNode *Node2 = new TreeNode(9);TreeNode *Node3 = new TreeNode(20);TreeNode *Node4 = new TreeNode(15);TreeNode *Node5 = new TreeNode(7);Node1->left = Node2;Node1->right = Node3;Node3->left = Node4;Node3->right = Node5;Solution S1;bool res = S1.isBalanced(Node1);if(res) std::cout << "true" << std::endl;else std::cout << "false" << std::endl;return 0;
}

10--二叉树的所有路径

主要思路：

        递归记录路径；

#include <iostream>
#include <vector>
#include <string>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:std::vector<std::string> binaryTreePaths(TreeNode* root) {std::vector<std::string> res;if(root == nullptr) return res;std::string path = "";dfs(root, res, path);return res;}void dfs(TreeNode *root, std::vector<std::string>& res, std::string path){if(root == nullptr) return;path += std::to_string(root->val);if(root->left == nullptr && root->right == nullptr) { // 叶子节点，回收路径res.push_back(path);return;}else path += "->";dfs(root->left, res, path);dfs(root->right, res, path);}
};int main(int argc, char* argv[]){// root = [1,2,3,null,5]TreeNode *Node1 = new TreeNode(1);TreeNode *Node2 = new TreeNode(2);TreeNode *Node3 = new TreeNode(3);TreeNode *Node4 = new TreeNode(5);Node1->left = Node2;Node1->right = Node3;Node2->right = Node4;Solution S1;std::vector<std::string> res = S1.binaryTreePaths(Node1);for(auto path : res) std::cout << path << std::endl;return 0;
}

11--左叶子之和

主要思路：

        递归到叶子节点的上一层，返回其左叶子之和；

#include <iostream>
#include <vector>
#include <string>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:int sumOfLeftLeaves(TreeNode* root) {if(root == nullptr) return 0;return dfs(root);}int dfs(TreeNode* root){if(root == nullptr) return 0;if(root->left == nullptr && root->right == nullptr) return 0;int sum = 0;if(root->left != nullptr && root->left->left == nullptr && root->left->right == nullptr){sum = root->left->val;}int left = dfs(root->left);int right = dfs(root->right);return left + right + sum;}
};int main(int argc, char* argv[]){// root = [3,9,20,null,null,15,7]TreeNode *Node1 = new TreeNode(3);TreeNode *Node2 = new TreeNode(9);TreeNode *Node3 = new TreeNode(20);TreeNode *Node4 = new TreeNode(15);TreeNode *Node5 = new TreeNode(7);Node1->left = Node2;Node1->right = Node3;Node3->left = Node4;Node3->right = Node5;Solution S1;int res = S1.sumOfLeftLeaves(Node1);std::cout << res << std::endl;return 0;
}

12--找树左下角的值

主要思路：

        递归到最大深度层，优先返回最左边的节点值，即递归时优先搜索左子树；

#include <iostream>
#include <vector>
#include <limits.h>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:int findBottomLeftValue(TreeNode* root) {if(root == nullptr) return 0;int max_height = INT_MIN;int result = 0;dfs(root, 0, max_height, result);return result;}void dfs(TreeNode* root, int curheight, int& max_height, int& res){if(root == nullptr) return;if(root->left == nullptr && root->right == nullptr){ // 叶子节点if(curheight + 1 > max_height){max_height = curheight + 1;res = root->val;return;}}dfs(root->left, curheight+1, max_height, res);dfs(root->right, curheight+1, max_height, res);  }
};int main(int argc, char* argv[]){// root = [3,9,20,null,null,15,7]TreeNode *Node1 = new TreeNode(2);TreeNode *Node2 = new TreeNode(1);TreeNode *Node3 = new TreeNode(3);Node1->left = Node2;Node1->right = Node3;Solution S1;int res = S1.findBottomLeftValue(Node1);std::cout << res << std::endl;return 0;
}

13--路径总和

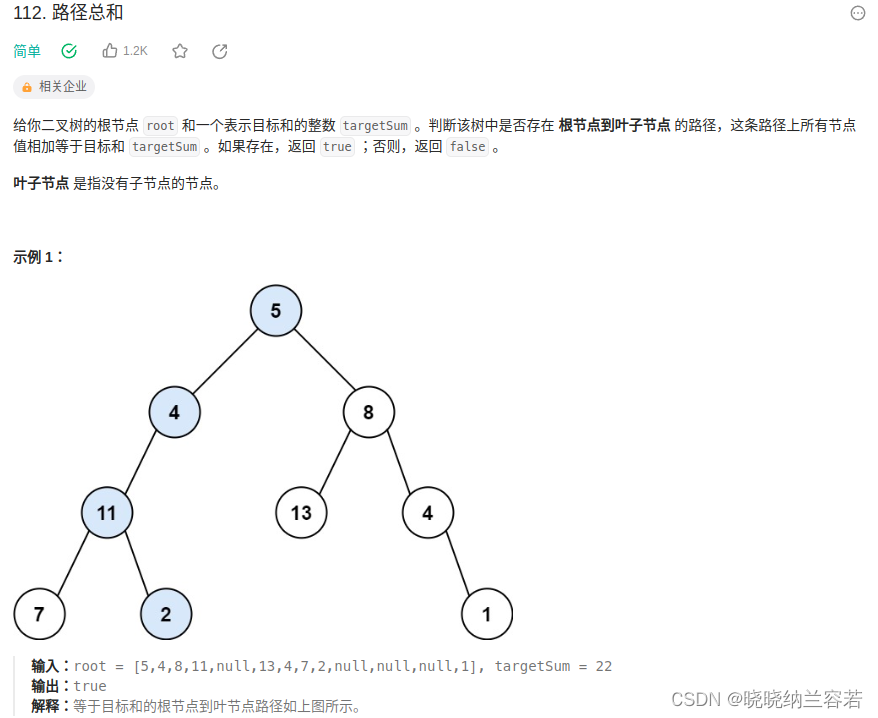
主要思路：

        递归搜索，判断路径和是否等于目标值即可；

#include <iostream>
#include <vector>
#include <limits.h>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:bool hasPathSum(TreeNode* root, int targetSum) {if(root == nullptr) return false;return dfs(root, targetSum);}bool dfs(TreeNode* root, int targetSum){if(root == nullptr) return false;if(root->left == nullptr && root->right == nullptr && targetSum == root->val){return true;}bool left = dfs(root->left, targetSum - root->val);if(left) return true;bool right = dfs(root->right, targetSum - root->val);if(right) return true;return false;}
};int main(int argc, char* argv[]){// root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22TreeNode *Node1 = new TreeNode(5);TreeNode *Node2 = new TreeNode(4);TreeNode *Node3 = new TreeNode(8);TreeNode *Node4 = new TreeNode(11);TreeNode *Node5 = new TreeNode(13);TreeNode *Node6 = new TreeNode(4);TreeNode *Node7 = new TreeNode(7);TreeNode *Node8 = new TreeNode(2);TreeNode *Node9 = new TreeNode(1);Node1->left = Node2;Node1->right = Node3;Node2->left = Node4;Node3->left = Node5;Node3->right = Node6;Node4->left = Node7;Node4->right = Node8;Node6->right = Node9;int target = 22;Solution S1;bool res = S1.hasPathSum(Node1, target);if(res) std::cout << "True" << std::endl;else std::cout << "false" << std::endl;return 0;
}

14--从中序与后序遍历序列构造二叉树

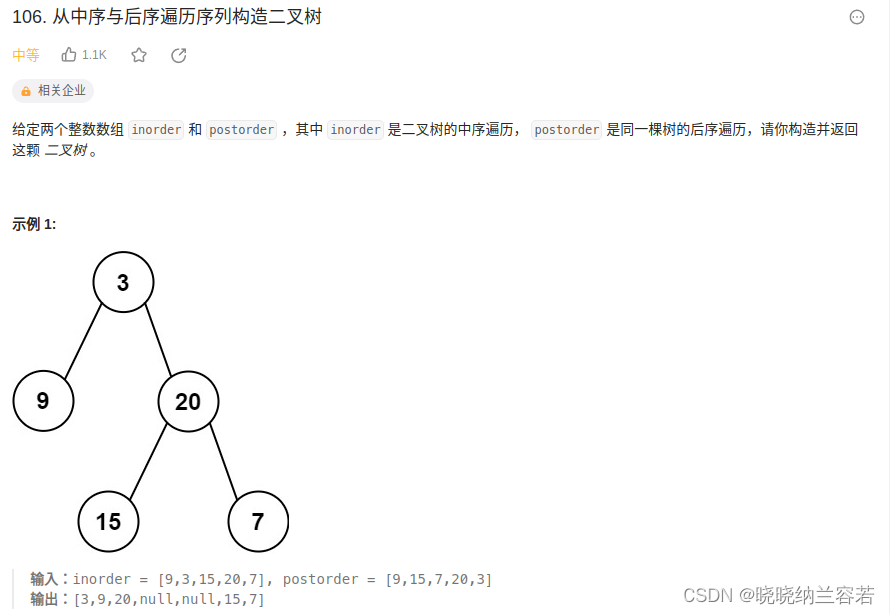
主要思路：

        中序遍历的顺序为：左→根→右，后序遍历的顺序为：左→右→根；即后序遍历的最后一个节点是根节点，因此可以根据根节点来划分中序遍历，将其划分为左子树和右子树，再根据左右子树的大小来划分后序遍历，递归构建二叉树；

#include <iostream>
#include <vector>
#include <queue>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:TreeNode* buildTree(std::vector<int>& inorder, std::vector<int>& postorder) {TreeNode *root = dfs(inorder, postorder);return root;}TreeNode* dfs(std::vector<int>& inorder, std::vector<int>& postorder){if(postorder.size() == 0) return nullptr;TreeNode *root = new TreeNode(postorder[postorder.size() - 1]); // 根节点if(postorder.size() == 1) return root;// 划分中序遍历int idx;for(idx = 0; idx < inorder.size(); idx++){if(inorder[idx] == root->val) break; // 找到中序遍历的根节点}// 划分后序遍历std::vector<int> left_inorder(inorder.begin(), inorder.begin()+idx); // 左子树的中序std::vector<int> right_inorder(inorder.begin()+idx+1, inorder.end()); // 右子树的中序std::vector<int> left_postorder(postorder.begin(), postorder.begin() + left_inorder.size()); // 左子树的后序std::vector<int> right_postorder(postorder.begin() + left_inorder.size(), postorder.end() - 1); // 右子树的后序root->left = dfs(left_inorder, left_postorder);root->right = dfs(right_inorder, right_postorder);return root;}
};int main(int argc, char* argv[]){// inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]std::vector<int> inorder = {9, 3, 15, 20, 7};std::vector<int> postorder = {9, 15, 7, 20, 3};Solution S1;TreeNode *root = S1.buildTree(inorder, postorder);// 层次遍历std::queue<TreeNode*> q;q.push(root);while(!q.empty()){TreeNode *tmp = q.front();q.pop();std::cout << tmp->val << " ";if(tmp->left != nullptr) q.push(tmp->left);if(tmp->right != nullptr) q.push(tmp->right);}std::cout << std::endl;return 0;
}

15--最大二叉树

主要思路：

        递归构建二叉树，首先寻找数组中的最大值，根据最大值划分左子树和右子树，递归构建左子树和右子树；

#include <iostream>
#include <vector>
#include <queue>
#include <limits.h>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:TreeNode* constructMaximumBinaryTree(std::vector<int>& nums) {TreeNode *root = dfs(nums);return root;}TreeNode* dfs(std::vector<int>& nums){if(nums.size() == 1){TreeNode* root = new TreeNode(nums[0]);return root;}// 遍历寻找最大值int max_idx = 0, max_value = INT_MIN;for(int i = 0; i < nums.size(); i++){if(nums[i] > max_value) {max_value = nums[i];max_idx = i;}}TreeNode *root = new TreeNode(nums[max_idx]);if(max_idx > 0){std::vector<int> left_nums(nums.begin(), nums.begin() + max_idx);root->left = dfs(left_nums);}if(max_idx < nums.size() - 1){std::vector<int> right_nums(nums.begin() + max_idx + 1, nums.end());root->right = dfs(right_nums);}return root;}
};int main(int argc, char* argv[]){// nums = [3,2,1,6,0,5]std::vector<int> nums = {3, 2, 1, 6, 0, 5};Solution S1;TreeNode *root = S1.constructMaximumBinaryTree(nums);// 层次遍历std::queue<TreeNode*> q;q.push(root);while(!q.empty()){TreeNode *tmp = q.front();q.pop();std::cout << tmp->val << " ";if(tmp->left != nullptr) q.push(tmp->left);if(tmp->right != nullptr) q.push(tmp->right);}std::cout << std::endl;return 0;
}

16--合并二叉树

主要思路：

        递归构建二叉树，两颗子树均不为 null 时，则构建新节点，其值为传入的两根节点之和；

        当其中一颗子树为空时，返回另一颗子树；

#include <iostream>
#include <vector>
#include <queue>
#include <limits.h>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {return dfs(root1, root2);}TreeNode* dfs(TreeNode* root1, TreeNode* root2){if(root1 == nullptr) return root2;if(root2 == nullptr) return root1;TreeNode *root = new TreeNode(root1->val + root2->val);root->left = dfs(root1->left, root2->left);root->right = dfs(root1->right, root2->right);return root;}    
};int main(int argc, char* argv[]){// root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]TreeNode* Node1_1 = new TreeNode(1);TreeNode* Node1_2 = new TreeNode(3);TreeNode* Node1_3 = new TreeNode(2);TreeNode* Node1_4 = new TreeNode(5);Node1_1->left = Node1_2;Node1_1->right = Node1_3;Node1_2->left = Node1_4;TreeNode* Node2_1 = new TreeNode(2);TreeNode* Node2_2 = new TreeNode(1);TreeNode* Node2_3 = new TreeNode(3);TreeNode* Node2_4 = new TreeNode(4);TreeNode* Node2_5 = new TreeNode(7);Node2_1->left = Node2_2;Node2_1->right = Node2_3;Node2_2->right = Node2_4;Node2_3->right = Node2_5;Solution S1;TreeNode *root = S1.mergeTrees(Node1_1, Node2_1);// 层次遍历std::queue<TreeNode*> q;q.push(root);while(!q.empty()){TreeNode *tmp = q.front();q.pop();std::cout << tmp->val << " ";if(tmp->left != nullptr) q.push(tmp->left);if(tmp->right != nullptr) q.push(tmp->right);}std::cout << std::endl;return 0;
}

17--二叉搜索树中的搜索

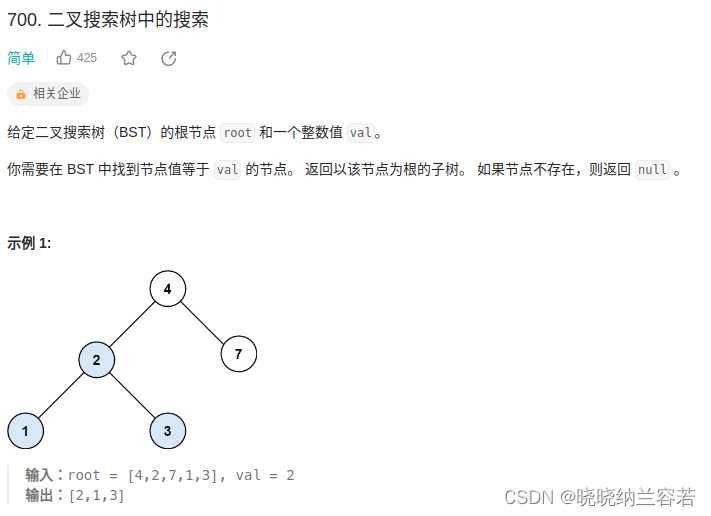
主要思路：

        根据节点大小，递归从左子树或者右子树寻找；

#include <iostream>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:TreeNode* searchBST(TreeNode* root, int val) {return dfs(root, val);}TreeNode* dfs(TreeNode* root, int val){if(root == nullptr || root->val == val) return root;if(root->val > val){return dfs(root->left, val);}else return dfs(root->right, val);}
};int main(int argc, char* argv[]){// root = [4,2,7,1,3], val = 2TreeNode *Node1 = new TreeNode(4);TreeNode *Node2 = new TreeNode(2);TreeNode *Node3 = new TreeNode(7);TreeNode *Node4 = new TreeNode(1);TreeNode *Node5 = new TreeNode(3);Node1->left = Node2;Node1->right = Node3;Node2->left = Node4;Node2->right = Node5;int val = 2;Solution S1;TreeNode *res = S1.searchBST(Node1, val);if(res == nullptr) std::cout << "" << std::endl;else std::cout << res->val << std::endl;return 0;
}

18--验证二叉搜索树

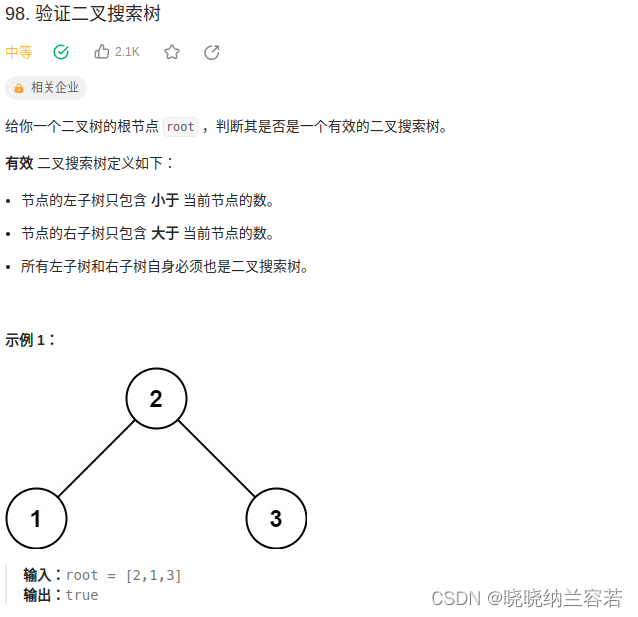
主要思路：

        递归判断，确保自下而上左子树节点都小于根节点，右子树节点都大于根节点；

#include <iostream>
#include <limits.h>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:bool isValidBST(TreeNode* root) {long long max_value = LONG_MAX, min_value = LONG_MIN;return dfs(root, max_value, min_value);}bool dfs(TreeNode *root, long long max_value, long long min_value){if(root == nullptr) return true;if(root->val >= max_value || root->val <= min_value) return false;bool left = dfs(root->left, root->val, min_value);bool right = dfs(root->right, max_value, root->val);return left && right;}
};int main(int argc, char* argv[]){// root = [2, 1, 3]TreeNode *Node1 = new TreeNode(2);TreeNode *Node2 = new TreeNode(1);TreeNode *Node3 = new TreeNode(3);Node1->left = Node2;Node1->right = Node3;Solution S1;bool res = S1.isValidBST(Node1);if(res) std::cout << "true" << std::endl;else std::cout << "false" << std::endl;return 0;
}

19--二叉搜索树的最小绝对差

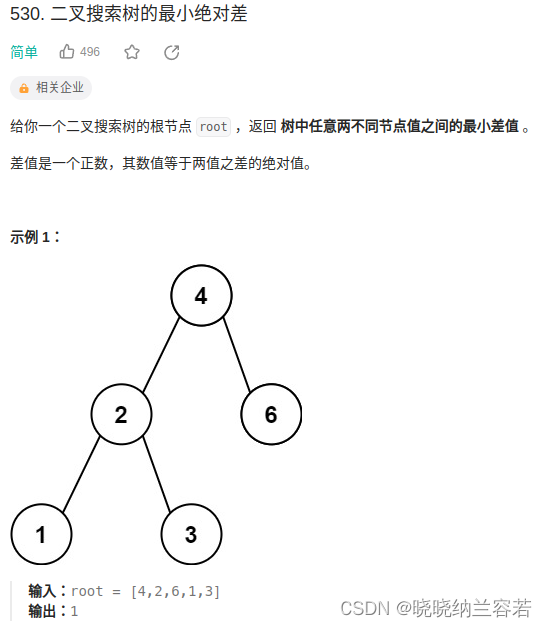
主要思路1：

        利用中序遍历将二叉搜索树的元素存放在一个递增的数组中，然后遍历递增数组，计算相邻两节点的差值即可；

#include <iostream>
#include <limits.h>
#include <vector>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:int getMinimumDifference(TreeNode* root) {std::vector<int> res;int min = INT_MAX;dfs(root, res);for(int i = 1; i < res.size(); i++){if(res[i] - res[i-1] < min){min = res[i] - res[i-1];}}return min;}void dfs(TreeNode *root, std::vector<int> &res){if(root == nullptr) return;dfs(root->left, res);res.push_back(root->val);dfs(root->right, res);}
};int main(int argc, char* argv[]){// root = [4,2,6,1,3]TreeNode *Node1 = new TreeNode(4);TreeNode *Node2 = new TreeNode(2);TreeNode *Node3 = new TreeNode(6);TreeNode *Node4 = new TreeNode(1);TreeNode *Node5 = new TreeNode(3);Node1->left = Node2;Node1->right = Node3;Node2->left = Node4;Node2->right = Node5;Solution S1;int res = S1.getMinimumDifference(Node1);std::cout << res << std::endl;return 0;
}

主要思路2：

        利用双指针递归，记录中序遍历的前一个节点和当前节点，计算两个节点的差值，并更新最小值即可；

#include <iostream>
#include <limits.h>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:int getMinimumDifference(TreeNode* root) {dfs(root);return min;}void dfs(TreeNode *cur){if(cur == nullptr) return;dfs(cur->left);if(pre != nullptr){min = std::min(min, cur->val - pre->val);}pre = cur;dfs(cur->right);}private:int min = INT_MAX;TreeNode *pre = nullptr;
};int main(int argc, char* argv[]){// root = [4,2,6,1,3]TreeNode *Node1 = new TreeNode(4);TreeNode *Node2 = new TreeNode(2);TreeNode *Node3 = new TreeNode(6);TreeNode *Node4 = new TreeNode(1);TreeNode *Node5 = new TreeNode(3);Node1->left = Node2;Node1->right = Node3;Node2->left = Node4;Node2->right = Node5;Solution S1;int res = S1.getMinimumDifference(Node1);std::cout << res << std::endl;return 0;
}

20--二叉搜索树中的众数

主要思路：

        基于双指针中序遍历二叉搜索树，判断pre指针和cur指针指向的节点是否相同，如果相同，则当前节点的 count++，否则 count = 1；

        当某个节点的出现频率与max_count相同时，将其放入结果数组；

        更新众数时需要清空结果数组，并放入最大众数对应的节点；

#include <iostream>
#include <vector>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:std::vector<int> findMode(TreeNode* root) {dfs(root);return res;}void dfs(TreeNode* cur){if(cur == nullptr) return;// 左dfs(cur->left);if(pre == nullptr || cur->val != pre->val){count = 1;}else{count++;}if(count == max_count) res.push_back(cur->val);if(count > max_count){max_count = count;res.clear();res.push_back(cur->val);}pre = cur; // 双指针dfs(cur->right);}private:int max_count = 0;int count = 0;std::vector<int> res;TreeNode *pre = nullptr;
};int main(int argc, char* argv[]){// root = [1,null,2,2]TreeNode *Node1 = new TreeNode(1);TreeNode *Node2 = new TreeNode(2);TreeNode *Node3 = new TreeNode(2);Node1->right = Node2;Node2->left = Node3;Solution S1;std::vector<int> res = S1.findMode(Node1);for(int v : res) std::cout << v << " ";std::cout << std::endl;return 0;
}

21--二叉树的最近公共祖先

主要思路：

        递归自底向上寻找，找到目标节点就返回；对于一个节点，若其左右子树均找到目标节点，则该节点即为最近公共祖先；

        若只有一颗子树能找到目标节点，则该子树的返回结果就是最近公共祖先；

#include <iostream>
#include <string>
#include <vector>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};class Solution {
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {TreeNode* res = dfs(root, p, q);return res;}TreeNode* dfs(TreeNode* root, TreeNode* p, TreeNode* q){if(root == nullptr) return nullptr;if(root->val == p->val || root->val == q->val) return root;TreeNode* left = dfs(root->left, p, q);TreeNode* right = dfs(root->right, p, q);if(left != nullptr && right != nullptr) return root;else if(left != nullptr && right == nullptr) return left;else return right;}
};int main(int argc, char* argv[]){// root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1TreeNode* Node1 = new TreeNode(3);TreeNode* Node2 = new TreeNode(5);TreeNode* Node3 = new TreeNode(1);TreeNode* Node4 = new TreeNode(6);TreeNode* Node5 = new TreeNode(2);TreeNode* Node6 = new TreeNode(0);TreeNode* Node7 = new TreeNode(8);TreeNode* Node8 = new TreeNode(7);TreeNode* Node9 = new TreeNode(4);Node1->left = Node2;Node1->right = Node3;Node2->left = Node4;Node2->right = Node5;Node3->left = Node6;Node3->right  = Node7;Node5->left = Node8;Node5->right = Node9;Solution S1;TreeNode *res = S1.lowestCommonAncestor(Node1, Node2, Node3);if(res != nullptr) std::cout << res->val << std::endl;else std::cout << "null" << std::endl;return 0;
}

22--二叉搜索树的最近公共祖先

主要思路：

        递归寻找，根据节点大小判断在左子树还是右子树寻找目标节点；

        对于一个节点，假如其值在两个目标节点中间，则该节点为最近公共祖先；

#include <iostream>
#include <string>
#include <vector>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};class Solution {
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {TreeNode* res = dfs(root, p, q);return res;}TreeNode* dfs(TreeNode* root, TreeNode* p, TreeNode* q){if(root == nullptr) return nullptr;if(root->val > p->val && root->val > q->val){return dfs(root->left, p, q);}else if(root->val < p->val && root->val < q->val){return dfs(root->right, p, q);}else return root;}
};int main(int argc, char* argv[]){// root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8TreeNode* Node1 = new TreeNode(6);TreeNode* Node2 = new TreeNode(2);TreeNode* Node3 = new TreeNode(8);TreeNode* Node4 = new TreeNode(0);TreeNode* Node5 = new TreeNode(4);TreeNode* Node6 = new TreeNode(7);TreeNode* Node7 = new TreeNode(9);TreeNode* Node8 = new TreeNode(3);TreeNode* Node9 = new TreeNode(5);Node1->left = Node2;Node1->right = Node3;Node2->left = Node4;Node2->right = Node5;Node3->left = Node6;Node3->right  = Node7;Node5->left = Node8;Node5->right = Node9;Solution S1;TreeNode *res = S1.lowestCommonAncestor(Node1, Node2, Node3);if(res != nullptr) std::cout << res->val << std::endl;else std::cout << "null" << std::endl;return 0;
}

23--二叉搜索树中的插入操作

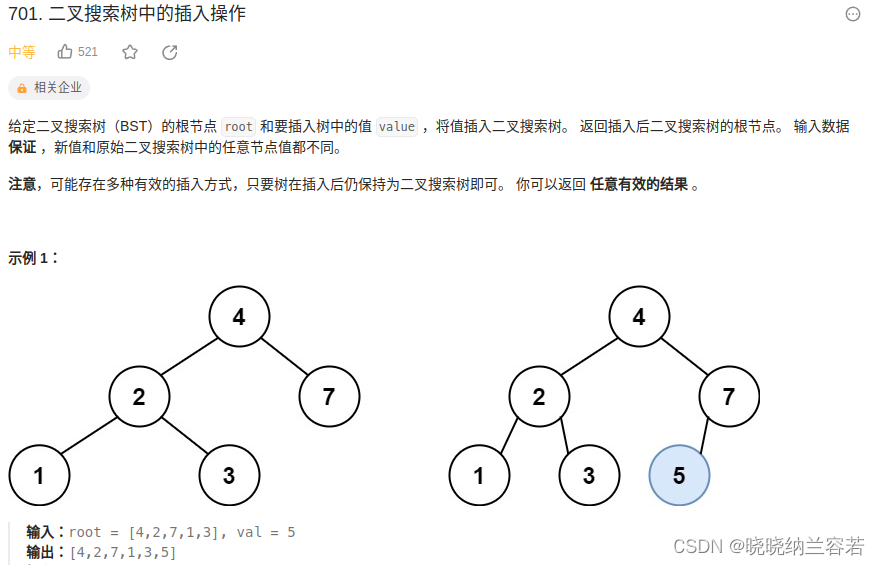
主要思路：

        任意一个节点的插入位置都能在叶子节点上找到，因此只需要递归遍历找到合适的叶子节点位置，将插入节点放到叶子节点位置即可；

#include <iostream>
#include <vector>
#include <queue>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:TreeNode* insertIntoBST(TreeNode* root, int val) {return dfs(root, val);}TreeNode* dfs(TreeNode* root, int val){if(root == nullptr){ // 找到叶子节点位置了TreeNode* target = new TreeNode(val);return target;}if(root->val > val){root->left = dfs(root->left, val);}else if(root->val < val){root->right = dfs(root->right, val);}return root;}
};int main(int argc, char* argv[]){TreeNode* Node1 = new TreeNode(4);TreeNode* Node2 = new TreeNode(2);TreeNode* Node3 = new TreeNode(7);TreeNode* Node4 = new TreeNode(1);TreeNode* Node5 = new TreeNode(3);Node1->left = Node2;Node1->right = Node3;Node2->left = Node4;Node2->right = Node5;int val = 5;Solution S1;TreeNode *res = S1.insertIntoBST(Node1, val);// 层次遍历std::queue<TreeNode *> q;q.push(res);while(!q.empty()){TreeNode* tmp = q.front();q.pop();std::cout << tmp->val << " ";if(tmp->left != nullptr){q.push(tmp->left);}if(tmp->right != nullptr){q.push(tmp->right);}}std::cout << std::endl;return 0;
}

24--删除二叉搜索树中的节点

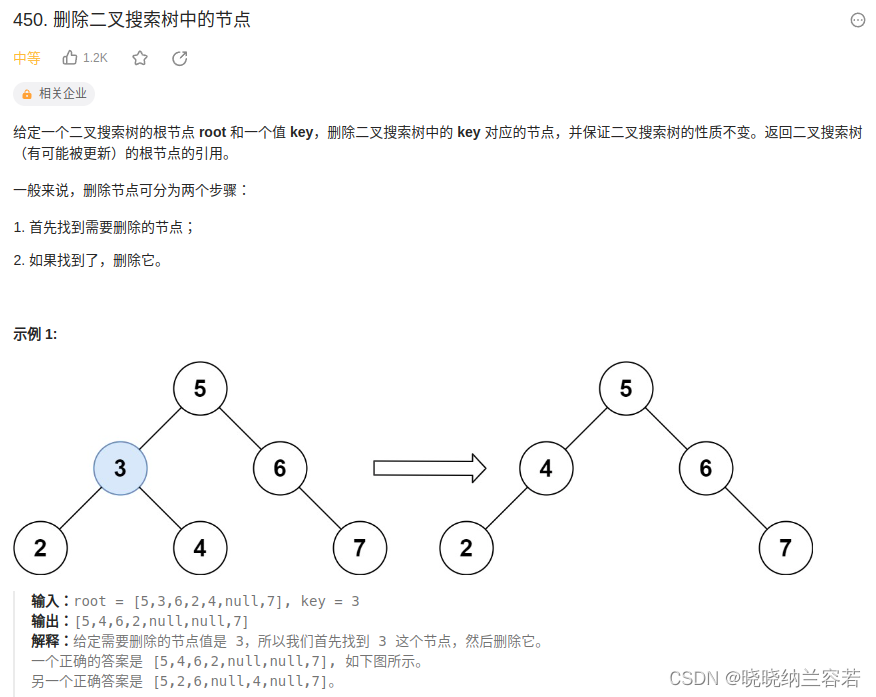
主要思路：

        删除节点有以下 5 种情况：

① 找不到删除的节点，返回 nullptr；

② 删除节点的左右孩子均为空（即为叶子节点），返回 nullptr；

③ 删除节点的左不空，右空，返回左孩子；

④ 删除节点的右不空，左空，返回右孩子；

⑤ 删除节点的左右均不空，记录删除节点的左孩子，然后递归删除节点的右孩子，找到最左边的叶子节点，将原先记录的删除节点的左孩子放到叶子结点的左孩子中；

#include <iostream>
#include <vector>
#include <queue>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:TreeNode* deleteNode(TreeNode* root, int key) {return dfs(root, key);}TreeNode* dfs(TreeNode* root, int key){if(root == nullptr) return nullptr; // 删除节点不存在if(root->val == key){ // 找到删除的叶子节点if(root->left == nullptr && root->right == nullptr){TreeNode *tmp = root;delete(tmp);return nullptr;}else if(root->left != nullptr && root->right == nullptr){TreeNode *tmp = root;TreeNode *left = root->left;delete(tmp);return left;}else if(root->left == nullptr && root->right != nullptr){TreeNode *tmp = root;TreeNode *right = root->right;delete(tmp);return right;}else{ // root->left != nullptr && root->right != nullptrTreeNode* left = root->left; // 记录其左子树TreeNode* right = root->right;TreeNode* cur = root->right;while(cur -> left != nullptr){ // 递归其右子树cur = cur->left;}cur->left = left; // 将左子树作为右子树最左边的叶子节点的左孩子delete(root);return right; // 返回右子树}}if(root->val > key) root->left = dfs(root->left, key);else root->right = dfs(root->right, key);return root;}  
};int main(int argc, char* argv[]){TreeNode* Node1 = new TreeNode(5);TreeNode* Node2 = new TreeNode(3);TreeNode* Node3 = new TreeNode(6);TreeNode* Node4 = new TreeNode(2);TreeNode* Node5 = new TreeNode(4);TreeNode* Node6 = new TreeNode(7);Node1->left = Node2;Node1->right = Node3;Node2->left = Node4;Node2->right = Node5;Node3->right = Node6;int key = 3;Solution S1;TreeNode *res = S1.deleteNode(Node1, key);// 层次遍历std::queue<TreeNode *> q;q.push(res);while(!q.empty()){TreeNode* tmp = q.front();q.pop();std::cout << tmp->val << " ";if(tmp->left != nullptr){q.push(tmp->left);}if(tmp->right != nullptr){q.push(tmp->right);}}std::cout << std::endl;return 0;
}

25--修建二叉搜索树

主要思路：

        对于小于左边界的节点，则其左子树所有节点都会小于左边界，因此可以舍弃；但仍需要递归判断其右子树；

        对于大于右边界的节点，则其右子树所有节点都会大于右边界，因此可以舍弃；但仍需要递归判断其左子树；

#include <iostream>
#include <vector>
#include <queue>struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution {
public:TreeNode* trimBST(TreeNode* root, int low, int high) {return dfs(root, low, high);}TreeNode* dfs(TreeNode* root, int low, int high){if(root == nullptr) return nullptr;if(root->val < low){return dfs(root->right, low, high);}if(root->val > high){return dfs(root->left, low, high);}root->left = dfs(root->left, low, high);root->right = dfs(root->right, low, high);return root;}
};int main(int argc, char* argv[]){// root = [1,0,2], low = 1, high = 2TreeNode* Node1 = new TreeNode(1);TreeNode* Node2 = new TreeNode(0);TreeNode* Node3 = new TreeNode(2);Node1->left = Node2;Node1->right = Node3;int low = 1, high = 2;Solution S1;TreeNode *res = S1.trimBST(Node1, low, high);// 层次遍历std::queue<TreeNode *> q;q.push(res);while(!q.empty()){TreeNode* tmp = q.front();q.pop();std::cout << tmp->val << " ";if(tmp->left != nullptr){q.push(tmp->left);}if(tmp->right != nullptr){q.push(tmp->right);}}std::cout << std::endl;return 0;
}

26--将有序数组转换为二叉搜索树

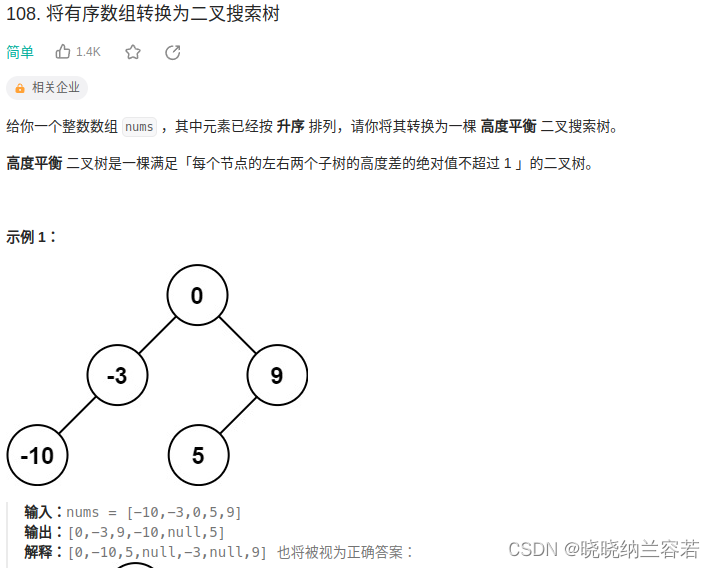
主要思路：

        

27--把二叉搜索树转换为累加树

主要思路：

        

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/121981.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

CS420 课程笔记 P5 - 内存编辑 数据类型

CS420 课程笔记 P5 - 内存编辑 数据类型

文章目录 IntroductionData typesBooleansNegative numbers (Signed integers)Floating-point numbers (fractional numbers) Unknown value scansHealth findingFloat finding (Player position hack / Teleport hack) Additional things Introduction 这节课将结束数据类型并…
阅读更多...
用Airtest快速实现手机文件读写与删除功能

用Airtest快速实现手机文件读写与删除功能

1. 前言 前几天有同学留言&#xff0c;能不能安排“读写手机文件”的示例。我们今天就来实现这个小功能。 当然&#xff0c;熟悉adb的同学&#xff0c;看到这个需求&#xff0c;肯定很开心&#xff0c;不就是一个 adb push 和 adb pull 嘛&#xff0c;非常简单呀。 确实如此…
阅读更多...
行业追踪，2023-08-31

行业追踪，2023-08-31

自动复盘 2023-08-31 凡所有相&#xff0c;皆是虚妄。若见诸相非相&#xff0c;即见如来。 k 线图是最好的老师&#xff0c;每天持续发布板块的rps排名&#xff0c;追踪板块&#xff0c;板块来开仓&#xff0c;板块去清仓&#xff0c;丢弃自以为是的想法&#xff0c;板块去留让…
阅读更多...
【数据结构】顺序表详解

【数据结构】顺序表详解

当我们写完通讯录后&#xff0c;顺序表肯定难不倒你&#xff0c;跟着小张一起来学习顺序表吧&#xff01; 线性表 线性表&#xff08;linear list&#xff09;是n个具有相同特性的数据元素的有限序列。 线性表是一种在实际中广泛使用的数据结构&#xff0c;常见的线性表&#x…
阅读更多...
Linux_VMware_虚拟机磁盘扩容

Linux_VMware_虚拟机磁盘扩容

来源文章 &#xff1a;VMware教学-虚拟机扩容篇_vmware虚拟机扩容_系统免驱动的博客-CSDN博客 由于项目逐步的完善&#xff0c;需要搭建的中间件&#xff0c;软件越来越多&#xff0c;导致以前虚拟机配置20G的内存不够用了&#xff0c;又不想重新创建新的虚拟机&#xff0c;退…
阅读更多...
pg_database中的datlastsysoid

pg_database中的datlastsysoid

一&#xff0c;关于 pg_database 在 PostgreSQL 中&#xff0c;对于在数据库集群内创建的每个数据库,其关键信息都会被保存到 pg_database 系统表中。 PostgreSQL 确保通过 pg_database 系统表持久化存储每个数据库的属性信息&#xff0c;以方便后续管理和使用。这也让 pg_da…
阅读更多...
go锁--读写锁

go锁--读写锁

每个锁分为读锁和写锁&#xff0c;写锁互斥 没有加写锁时&#xff0c;多个协程都可以加读锁 加了写锁时&#xff0c;无法加读锁&#xff0c;读协程排队等待 加了读锁&#xff0c;写锁排队等待 Mutex用来写协程之间互斥等待 读协程使用readerSem等待写锁的释放 写协程使用writer…
阅读更多...
Android Native Code开发学习（三）对java中的对象变量进行操作

Android Native Code开发学习（三）对java中的对象变量进行操作

Android Native Code开发学习&#xff08;三&#xff09; 本教程为native code学习笔记&#xff0c;希望能够帮到有需要的人 我的电脑系统为ubuntu 22.04&#xff0c;当然windows也是可以的&#xff0c;区别不大 对java中的对象变量进行操作 首先我们新建一个java的类 pub…
阅读更多...
多目标应用：基于多目标人工蜂鸟算法（MOAHA）的微电网多目标优化调度MATLAB

多目标应用：基于多目标人工蜂鸟算法（MOAHA）的微电网多目标优化调度MATLAB

一、微网系统运行优化模型 参考文献&#xff1a; [1]李兴莘,张靖,何宇,等.基于改进粒子群算法的微电网多目标优化调度[J].电力科学与工程, 2021, 37(3):7 二、多目标人工蜂鸟算法MOAHA 多目标人工蜂鸟算法&#xff08;multi-objective artificial hummingbird algorithm&…
阅读更多...
跨数据中心Multi-Fabric解决方案：L2和L3网络的高效连接和扩展

跨数据中心Multi-Fabric解决方案：L2和L3网络的高效连接和扩展

云数据中心里&#xff0c;为什么需要DCI互通&#xff1f; 云化数据中心&#xff0c;网络资源通过虚拟化技术形成资源池&#xff0c;实现业务与物理网络解耦&#xff0c;通过网络虚拟化&#xff0c;物理网络资源可以被分成多个虚拟网络资源&#xff0c;从而提高网络资源的使用效…
阅读更多...
设计模式之装饰者模式

设计模式之装饰者模式

文章目录 星巴克咖啡订单项目&#xff08;咖啡馆&#xff09;方案 1-解决星巴克咖啡订单项目方案 1-解决星巴克咖啡订单问题分析方案 2-解决星巴克咖啡订单(好点)方案 2-解决星巴克咖啡订单问题分析装饰者模式定义装饰者模式原理装饰者模式解决星巴克咖啡订单装饰者模式下的订单…
阅读更多...
【LeetCode算法系列题解】第51~55题

【LeetCode算法系列题解】第51~55题

CONTENTS LeetCode 51. N 皇后&#xff08;困难&#xff09;LeetCode 52. N 皇后 II&#xff08;困难&#xff09;LeetCode 53. 最大子序和&#xff08;中等&#xff09;LeetCode 54. 螺旋矩阵&#xff08;中等&#xff09;LeetCode 55. 跳跃游戏&#xff08;中等&#xff09; …
阅读更多...
跨站请求伪造（CSRF）攻击与防御原理

跨站请求伪造（CSRF）攻击与防御原理

跨站请求伪造&#xff08;CSRF&#xff09; 1.1 CSRF原理 1.1.1 基本概念 跨站请求伪造&#xff08;Cross Site Request Forgery&#xff0c;CSRF&#xff09;是一种攻击&#xff0c;它强制浏览器客户端用户在当前对其进行身份验证后的Web 应用程序上执行非本意操作的攻击&a…
阅读更多...
Debian离线安装mysql

Debian离线安装mysql

PS:虽然已经分享了很多安装各种环境订的教程&#xff0c;但是每个客户的环境不一样&#xff0c;那就得重新来一次&#xff0c;其实都是大同小异的&#xff0c;但是里面其实也是存在不少坑的&#xff0c;今天我们就来安装一个新的东西&#xff0c;Debian 11离线安装mysql,为什么…
阅读更多...
Linux命令200例：bc是用于数学计算的高级计算器

Linux命令200例：bc是用于数学计算的高级计算器

&#x1f3c6;作者简介&#xff0c;黑夜开发者&#xff0c;CSDN领军人物&#xff0c;全栈领域优质创作者✌。CSDN专家博主&#xff0c;阿里云社区专家博主&#xff0c;2023年6月csdn上海赛道top4。 &#x1f3c6;数年电商行业从业经验&#xff0c;历任核心研发工程师&#xff0…
阅读更多...
单片机通用学习-​什么是寄存器？​

单片机通用学习-​什么是寄存器？​

什么是寄存器&#xff1f; 寄存器是一种特殊的存储器&#xff0c;主要用于存储和检查微机的状态。CPU寄存器用于存储和检查CPU的状态&#xff0c;具体包括计算中途数据、程序因中断或子程序分支时的返回地址、计算结果为零时的负值、计算结果为零时的信息、进位值等。 由于CP…
阅读更多...
基于Yolov5的摄像头吸烟行为检测系统（pytoch）

基于Yolov5的摄像头吸烟行为检测系统（pytoch）

目录 1.数据集介绍 1.1数据集划分 1.2 通过voc_label.py生成txt 1.3 小目标定义 2.基于Yolov5的吸烟行为检测性能提升 2.1采用多尺度提升小目标检测精度 2.2 多尺度训练结果分析 2.3基于多尺度基础上加入BiFormer: 基于动态稀疏注意力构建高效金字塔网络架构 2.3.1 BiFo…
阅读更多...
css让元素保持等比例宽高

css让元素保持等比例宽高

使用新属性 aspect-ratio: 16/9; 代码示例 <style>div {width: 60%;/* 等比例宽高 */aspect-ratio: 16/9;background-color: red;margin: auto;}</style> </head><body><div></div> </body>示例 aspect-ratio兼容性
阅读更多...
分布式系统的多数据库，实现分布式事务回滚（1.7.0 seata整合2.0.4nacos）

分布式系统的多数据库，实现分布式事务回滚（1.7.0 seata整合2.0.4nacos）

正文 1、解决的应用场景是分布式事务&#xff0c;每个服务有独立的数据库。 2、例如&#xff1a;A服务的数据库是A1&#xff0c;B服务的数据库是B2&#xff0c;A服务通过feign接口调用B服务&#xff0c;B涉及提交数据到B2&#xff0c;业务是在B提交数据之后&#xff0c;在A服…
阅读更多...
SpringBoot集成WebSocket

SpringBoot集成WebSocket

SpringBoot集成WebSocket 项目结构图 项目架构图 前端项目 socket.js 注意前端这里的端口是9000, 路劲是ws开头 function createScoket(token){var socket;if(typeof(WebSocket) "undefined") {console.log("您的浏览器不支持WebSocket");}else{var ho…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023