题目
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
示例 1:
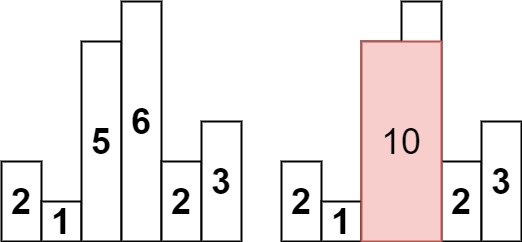
输入:heights = [2,1,5,6,2,3] 输出:10 解释:最大的矩形为图中红色区域,面积为 10
示例 2:
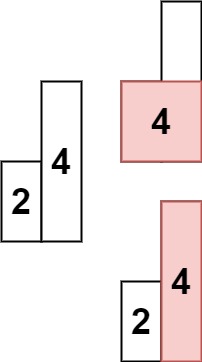
输入: heights = [2,4] 输出: 4
提示:
1 <= heights.length <=10^50 <= heights[i] <= 10^4
解答
源代码
class Solution {public int largestRectangleArea(int[] heights) {int[] left = new int[heights.length];int[] right = new int[heights.length];Deque<Integer> stack = new ArrayDeque<>();for (int i = 0; i < heights.length; i++) {while (!stack.isEmpty() && heights[stack.peek()] >= heights[i]) {stack.pop();}left[i] = (stack.isEmpty() ? -1 : stack.peek());stack.push(i);}stack.clear();for (int i = heights.length - 1; i > -1; i--) {while (!stack.isEmpty() && heights[stack.peek()] >= heights[i]) {stack.pop();}right[i] = (stack.isEmpty() ? heights.length : stack.peek());stack.push(i);}int res = 0;for (int i = 0; i < heights.length; i++) {res = Math.max(res, (right[i] - left[i] - 1) * heights[i]);}return res;}
}总结
最大矩形的高度一定是某个柱子的高度,所以我们只要把每个柱子的高度往两边延伸,记录下它们能达到的最大的宽度,计算出矩形面积。
利用暴力枚举虽然也能找到某个柱子两边小于它且离它最近的柱子,但这明显不太优雅,肯定不是最佳解法。
为了跳过不必要的比较,我们所需要用到的就是“单调栈”。栈中存放的是柱子对应的下标,从栈底到栈顶,下标单调递增,下标对应的柱子高度也单调递增。从左到右遍历到某个柱子时,要用它和栈顶下标对应的柱子高度比较,如果低于等于栈顶对应柱子,就出栈直到该柱子高于栈顶对应柱子,那么此时栈顶下标对应的柱子就是当前柱子左边小于它且离它最近的柱子。同理,得到右边的。
这样经过两次遍历,我们可以得到每个柱子左右两边的边界。这里有特殊情况,如果左右两边没有比自己低的柱子,那就将边界设为0 / heights.length。然后计算出以每个柱子高度为矩形高度得到的矩形面积,比较选出最大的面积。