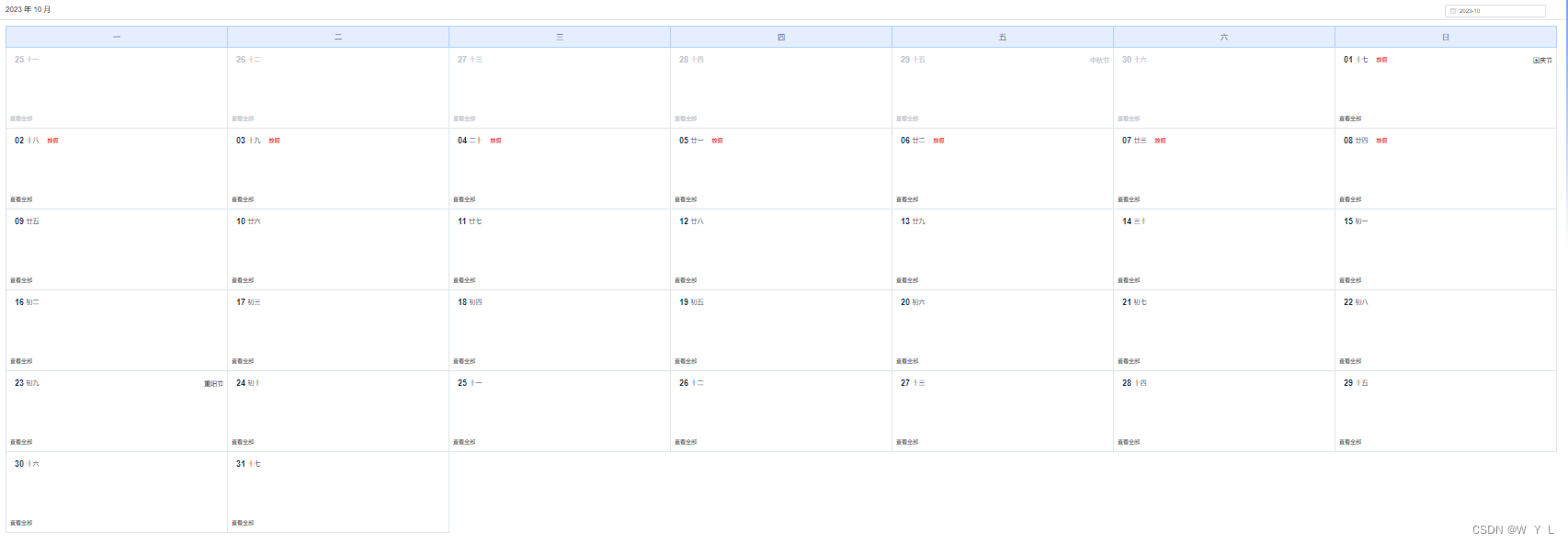
原创 | 文 BFT机器人 

《KPConv: Flexible and Deformable Convolution for Point Clouds》是一篇发表于2019年的研究论文，作者为Hugues Thomas、Charles R. Qi、Jean-Emmanuel Deschaud、Beatriz Marcotegui和François Goulette。这篇论文关注于点云数据上的卷积操作，提出了一种名为KPConv的卷积方法，旨在解决点云数据上的灵活性和可变形性问题。

01

背景

点云数据是从3D传感器（如激光雷达）获得的场景的一种表示形式，逐渐在自动驾驶、机器人导航、三维场景重建等领域得到广泛应用。因为点云数据直接捕捉了真实世界的几何信息，因此在处理三维信息方面具有独特的优势。传统的卷积神经网络（CNN）在图像领域获得了巨大成功，但直接将CNN应用于点云数据上存在一些挑战。点云数据是无序和不规则的，不同于像素网格。因此，需要设计新的卷积操作来适应点云数据的特点。点云数据中的物体形状和分布可能会因为姿态、视角和尺度的变化而产生巨大的变化。为了准确地捕捉这些变化，需要在点云上进行灵活的卷积操作，并能够处理可变形的形状。

该论文的研究背景强调了点云数据的特点、点云数据上的卷积问题以及灵活性与可变形性的需求，为提出新的KPConv方法提供了合理性和必要性。

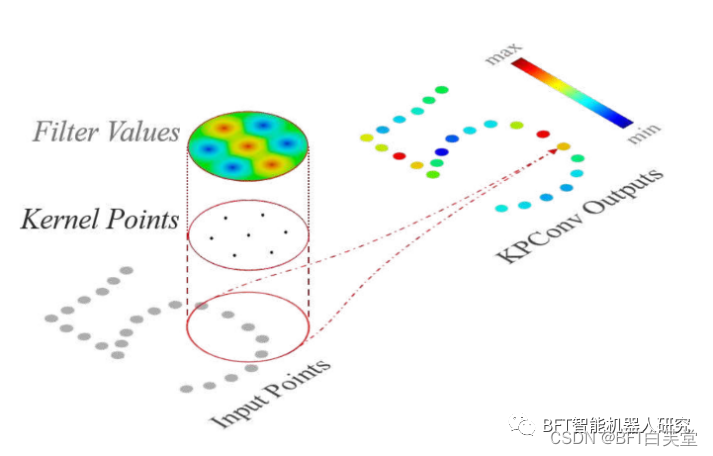
图1 用2D点表示KPConv

02

工作内容

论文的工作内容主要包括以下几个方面：

1、KPConv的设计与定义：论文提出了KPConv，即"Kernel Point Convolution"，这是一种基于核心点的卷积操作。核心点是预定义的一组点，它们的位置和形状可以自适应地进行调整。KPConv通过计算输入点云中的每个点与核心点之间的关系，实现了一种适应点云数据特点的卷积操作。

2、自适应核心点位置和形状：KPConv中的核心点不仅仅是静态的，它们的位置和形状可以根据输入点云的局部结构和变化进行自适应调整。这种自适应性使得KPConv能够灵活地捕捉点云数据中物体的形状变化和分布情况。

3、卷积过程：KPConv的卷积过程包括确定核心点、计算点云中每个点与核心点之间的关系、根据关系进行加权聚合等步骤。通过这一过程，KPConv可以在点云上有效地传播特征信息，并捕捉局部的几何结构。

4、实验验证：通过在不同的点云数据集上进行实验验证了KPConv的性能。实验结果表明，KPConv在点云分割和点云分类任务中取得了优越的结果，证明了其在处理点云数据上的卓越性能。

5、可视化分析：通过可视化分析展示了KPConv的效果，展示了其在不同场景中捕捉几何结构和变化的能力。这有助于更好地理解KPConv的工作原理和优势。

03

算法介绍

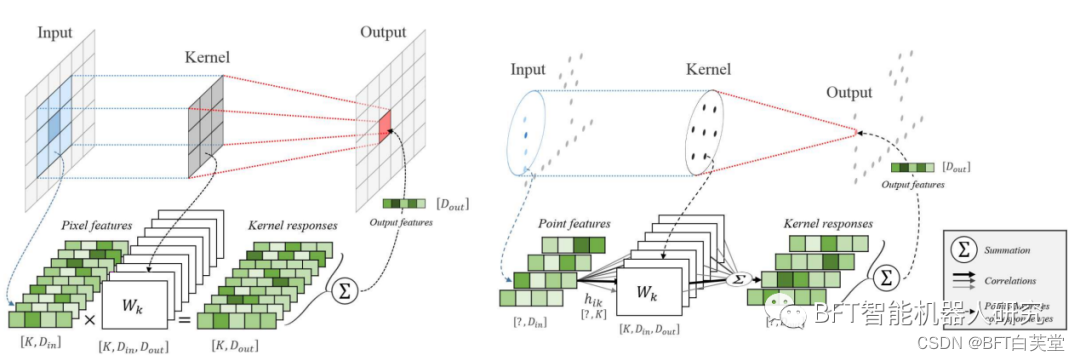
图2 KPConv工作流程

该论文提出了一种新的点卷积设计，称为可变形卷积（deformable KPConv）。该设计基于点云数据，通过在点云上定义核点来执行卷积操作。与传统的固定网格卷积相比，KPConv具有更大的灵活性，因为它可以使用任意数量的核点，并且这些点在空间上是连续的，可以通过网络进行学习。此外，KPConv还可以通过学习适应局部几何形状的核点来扩展到可变形卷积。具体步骤如下：

1、核心点的选择与定义：首先，选择一组核心点，这些点是预先定义的，并且可以分布在不同的形状上。对于每个核心点，定义一个局部坐标系，其中核心点为原点，坐标轴也可以自适应地根据局部点云的几何结构进行旋转。

2、关系计算：对于输入点云中的每个点，计算它与所有核心点之间的关系。这个关系可以用来描述该点与核心点之间的相对位置和距离。

3、权重计算：基于关系计算的结果，计算每个点与核心点之间的权重。权重用于将核心点的特征信息传递给输入点。

4、特征聚合：对于每个输入点，根据权重对核心点的特征进行加权聚合，生成该点的新特征表示。这样，每个点都会受到其周围核心点的影响，从而捕捉局部几何结构和特征信息。

5、网络结构与训练：在网络结构中，KPConv被用作一个模块，可以嵌入到不同的架构中。网络通过反向传播进行训练，优化KPConv中的权重和核心点的位置。

KPConv算法通过自适应的核心点和权重计算，以及特征聚合的方式，实现了在点云数据上的卷积操作。它能够有效地处理点云数据的无序性和不规则性，捕捉局部几何结构和特征信息，同时具有适应不同形状和分布的灵活性和可变形性。在实验中，KPConv在点云分类和点云分割等任务中表现出色，证明了其在点云数据上的有效性。

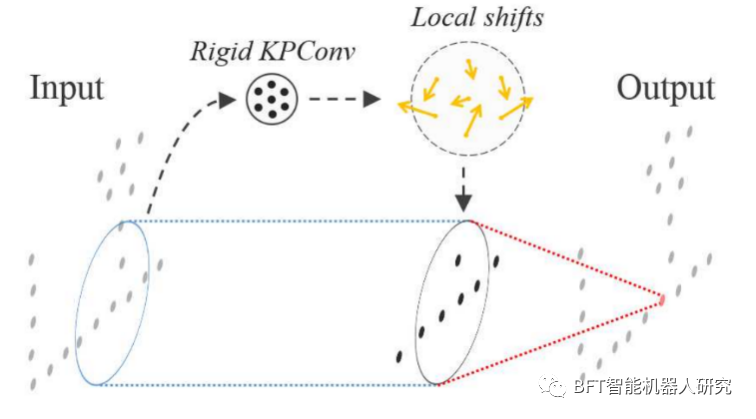
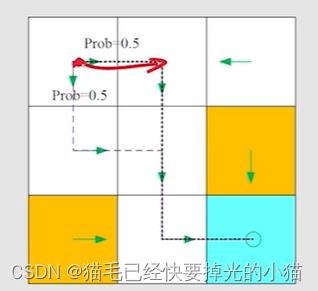
图3 用2D点表示KPConv可变形性

04

实验论述

论文的实验过程旨在验证提出的KPConv算法在点云分类和点云分割任务中的性能。以下是论文中实验过程的主要内容：

1、数据集选择：论文选择了一些常用的点云数据集，例如ModelNet40和ShapeNet，用于点云分类任务。对于点云分割任务，使用了Semantic3D和S3DIS数据集，这些数据集包含了具有不同类别的点云以及对应的标签信息。

2、网络架构搭建：在实验中，KPConv被嵌入到深度学习网络中，作为卷积操作的组成部分。具体的网络架构可以是基于PointNet、PointNet++等。论文中还可以对比使用传统的点云卷积方法进行性能比较，以显示KPConv的优越性。

3、训练与评估：使用选定的数据集和网络架构，将网络进行训练。训练过程中，使用损失函数对网络进行优化，以使其能够准确预测点云的类别或分割标签。在每个训练轮次结束后，使用验证集对网络进行评估，以监控性能的变化和收敛情况。

4、性能指标：对于点云分类任务，常用的性能指标包括准确率（Accuracy）等，用于评估网络对点云数据进行分类的能力。对于点云分割任务，可以使用IoU（Intersection over Union）等指标来衡量网络对点云的分割精度。

5、结果分析与对比：论文通过在测试集上的性能表现，对KPConv在点云分类和点云分割任务上的效果进行分析。还可能与其他点云卷积方法进行比较，以展示KPConv的优越性和性能提升。

6、可视化分析：为了更好地理解KPConv的工作原理，论文可能会进行可视化分析，展示KPConv如何捕捉点云数据中的几何结构和特征信息。

通过以上实验过程，论文可以验证提出的KPConv算法在点云分类和点云分割任务上的性能，并与现有的点云处理方法进行比较，从而证明其有效性和优越性。这些实验结果有助于向研究社区和实际应用中展示KPConv的实际价值。

05

结论

可变形KPConv是一种有效的点云卷积设计，具有灵活性、高效性和适应性，能够学习和适应核点，从而在分类和分割任务中优于现有的方法。论文还表明，可变形KPConv在大型和多样化的数据集上具有描述能力，可以在更大的数据集上发挥作用。此外，论文还提供了消融研究和可视化结果，以验证可变形KPConv的描述能力。

作者 | Azukii

排版 | 小河

审核 | 猫

若您对该文章内容有任何疑问，请与我们联系，我们将及时回应。如果想要了解更多的前沿资讯，记得点赞关注哦~