文章目录
- 写在前面
- Tag
- 题目来源
- 题目解读
- 解题思路
- 方法一:合并排序
- 方法二:双指针
- 方法三:原地操作-从前往后
- 方法四:原地操作-从后往前
- 写在最后
写在前面
本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢迎催更……
专栏内容以分析题目为主,并附带一些对于本题涉及到的数据结构等内容进行回顾与总结,文章结构大致如下,部分内容会有增删:
- Tag:介绍本题牵涉到的知识点、数据结构;
- 题目来源:贴上题目的链接,方便大家查找题目并完成练习;
- 题目解读:复述题目(确保自己真的理解题目意思),并强调一些题目重点信息;
- 解题思路:介绍一些解题思路,每种解题思路包括思路讲解、实现代码以及复杂度分析;
- 知识回忆:针对今天介绍的题目中的重点内容、数据结构进行回顾总结。
Tag
【双指针】【原地操作-从前往后】【原地操作-从后往前】【排序】【数组】
题目来源
面试经典 150 题——88. 合并两个有序数组

题目解读
给定两个有序数组 nums1 和 nums2,现在需要合并两个数组到 nums1 中,nums1 中已经预留了合并的位置。
解题思路
方法一:合并排序
将数组nums2 合并到 nums1 数组中的空位上,再利用 sort() 函数进行排序。
时间复杂度: O ( ( m + n ) l o g ( m + n ) ) O((m+n)log(m+n)) O((m+n)log(m+n)),快速排序的时间复杂度。
空间复杂度: O ( l o g ( m + n ) ) O(log(m+n)) O(log(m+n)),快速排序占用的空间。
方法二:双指针
维护一个临时数组,用来存放合并后的数组。
使用两个指针 i,j,分别指向两数组首元素,迭代比较 i、j 位置处元素大小,将小的元素依次存入临时数组。
最后,将临时数组中元素移植到 nums1 数组中。
时间复杂度 O ( m + n ) O(m+n) O(m+n)。
空间复杂度 O ( m + n ) O(m+n) O(m+n),因为需要一个临时数组,大小为 m + n m+n m+n。
方法三:原地操作-从前往后
首先,重新定义一下双指针 i 和 j 的含义,两指针分别表示指向数组 nums1 和 nums2 当前没有使用过的最小的元素,i 也表示当前最小元素将要放置的位置。
在方法二中,我们之所以使用了一个临时数组来存放较小的数字,是因为我们从前往后枚举比较两指针指向的元素得到较小值,如果直接合并到 nums1 数组中,可能会覆盖掉 nums1 中接下来将要比较的数字(这也是原地操作删除有序数组中的重复元素的思想,具体内容可见 图解【原地操作】删除有序数组中的重复元素)。
直接合并有问题,那么我们进行交换处理保留较大数,即交换 nums1[i] 和 nums2[j],交换了之后,我们将较小的数放置在数组 nums1 的 i 位置处,较大的数放置在数组 nums2 的 j 位置处。这时候还需要对数组 nums2 进行排序,每次交换数字之后都要进行排序操作。
因为我们的双指针都是指向当前数组中最小的数字,交换操作有可能破坏数组 nums2 的升序结构。
下面以图示形式进行演示:
(1)双指针从 0 位置开始;

(2)nums1[0] < nums2[0],右移 i 指针;
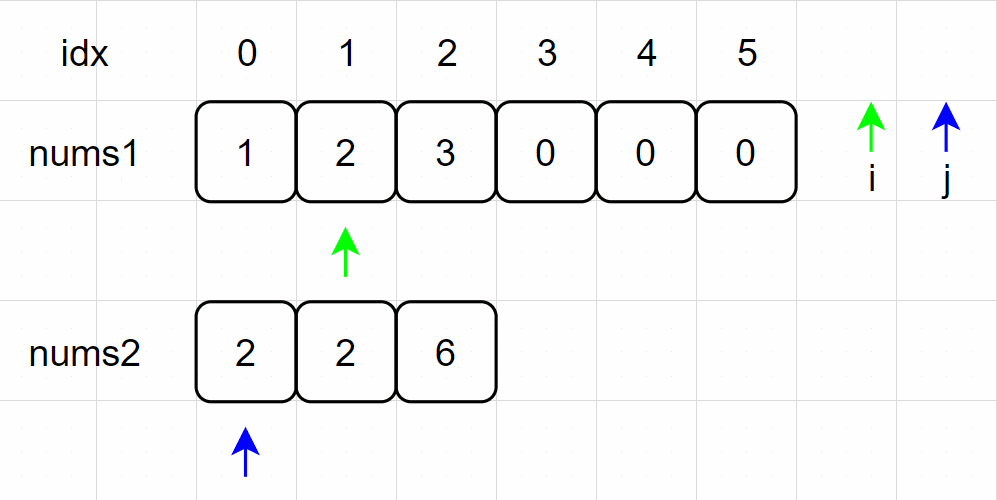
(3)nums1[1] = nums2[0],右移 i 指针;

(4)nums2[0] < nums1[2],交换数组中两元素;
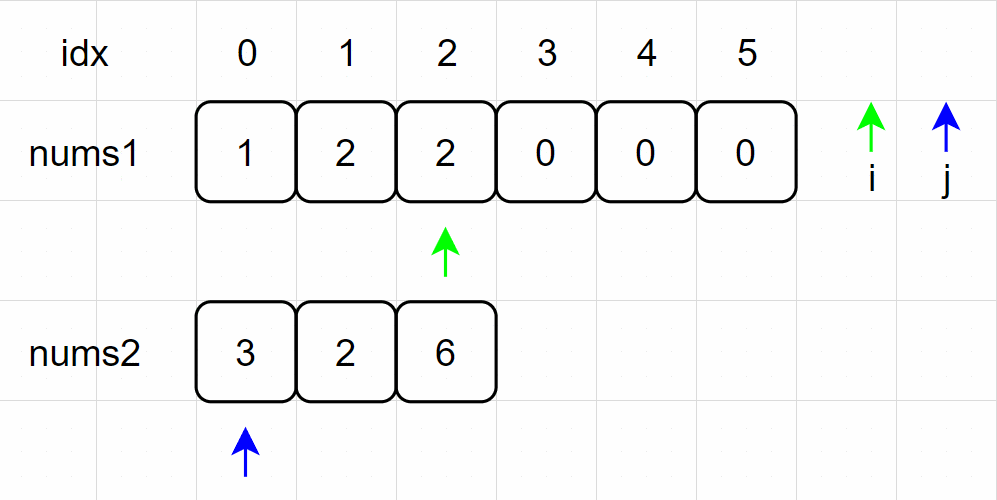
(5)nums2 数组的升序结构被破坏,需要进行升序排序;

(6)nums1[2] = nums2[0],右移 i 指针;
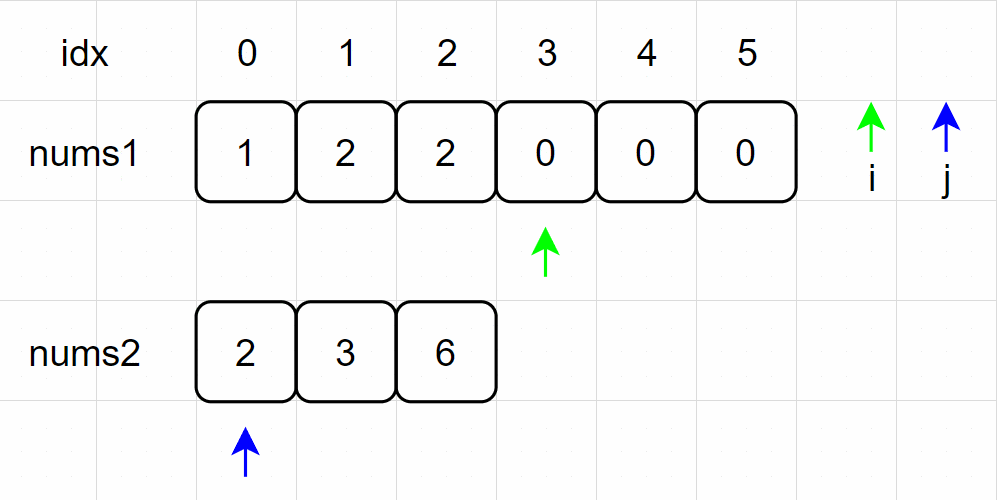
(7)数组 nums1 中前半部分数位已经填充完毕,后半部分占位符使用数组 nums2 填充,当前位置填充完毕之后,同时右移两指针;如此迭代填充,直至 j 指针越界,合并两个有序数组完成!

实现代码
class Solution {
public:void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {int i = 0, j = 0;while (j < n) {if (i >= m) {nums1[i] = nums2[j++];}else {if (nums1[i] > nums2[j]) {swap(nums1[i], nums2[j]);}sort(nums2.begin(), nums2.end());}++i;}}
};
时间复杂度: O ( m a x ( m , n l o g n ) ) O(max(m, nlogn)) O(max(m,nlogn))。
空间复杂度: O ( n l o g n ) O(nlogn) O(nlogn),快速排序占用的空间。
方法四:原地操作-从后往前
现在考虑从后往前处理,具体地维护三个指针,i 指向数组 nums1 比较元素的末尾即 m-n-1 位置,j 指针指向数组 nums2 比较元素的末尾即 n-1 位置,k 指针指向数组 nums1 的末尾即 m-1 位置。
我们比较 nums1[i] 和 nums2[j] 元素大小,将较大的元素放置在数组 nums1 的 k 位置处。
下面以图示形式进行演示:
(1)三指针初始化;

(2)nums1[2] < nums2[2] ,将较大的 nums2[2] 放置在 tail 处;
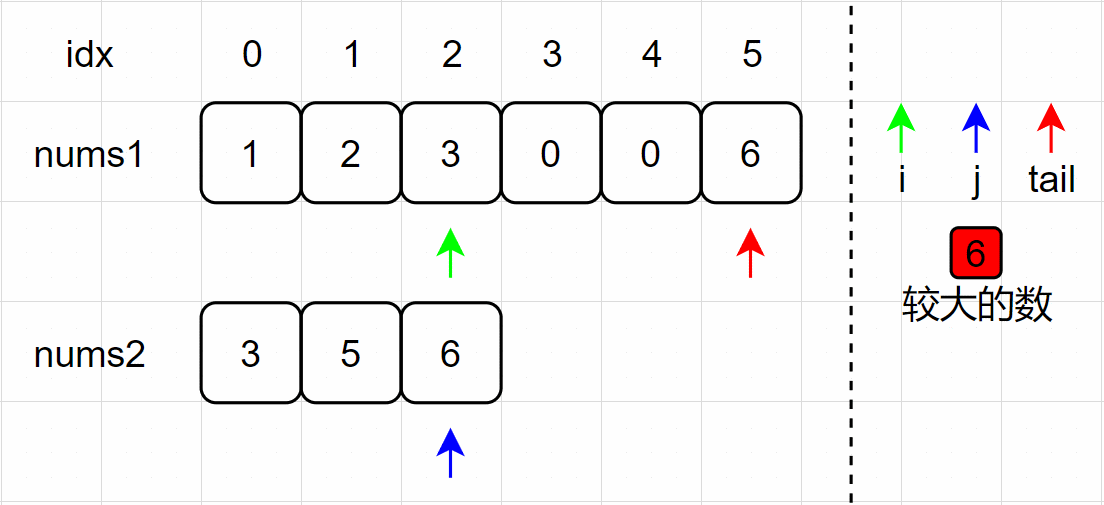
(3)j、tail 指针分别左移一个单位,为下次比较做准备;

(4) nums1[2] < nums2[1] ,将较大的 nums2[1] 放置在 tail 处;

(5)j、tail 指针分别左移一个单位,为下次比较做准备;
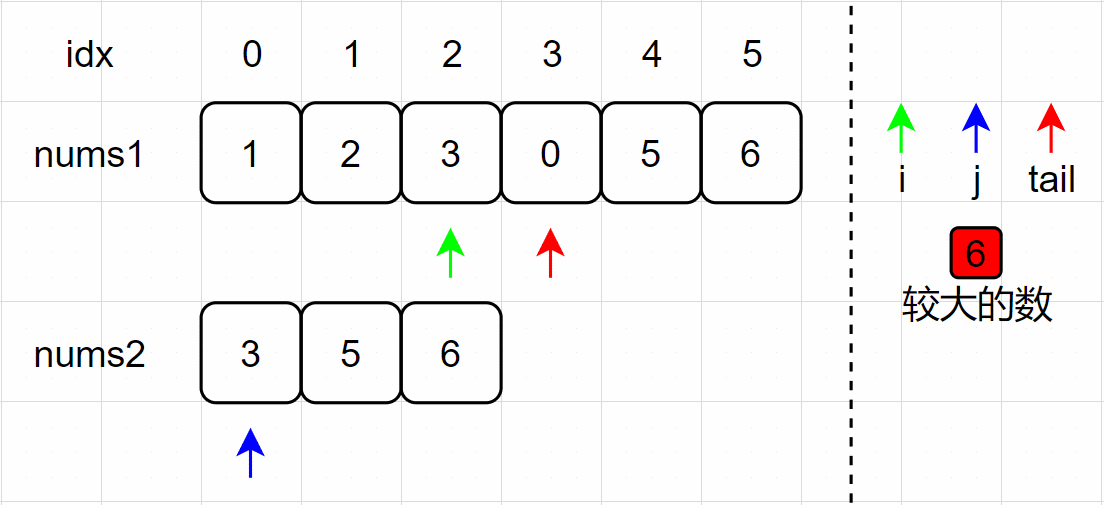
(6)nums1[2] = nums2[0] ,将 nums1[1] 放置在 tail 处;
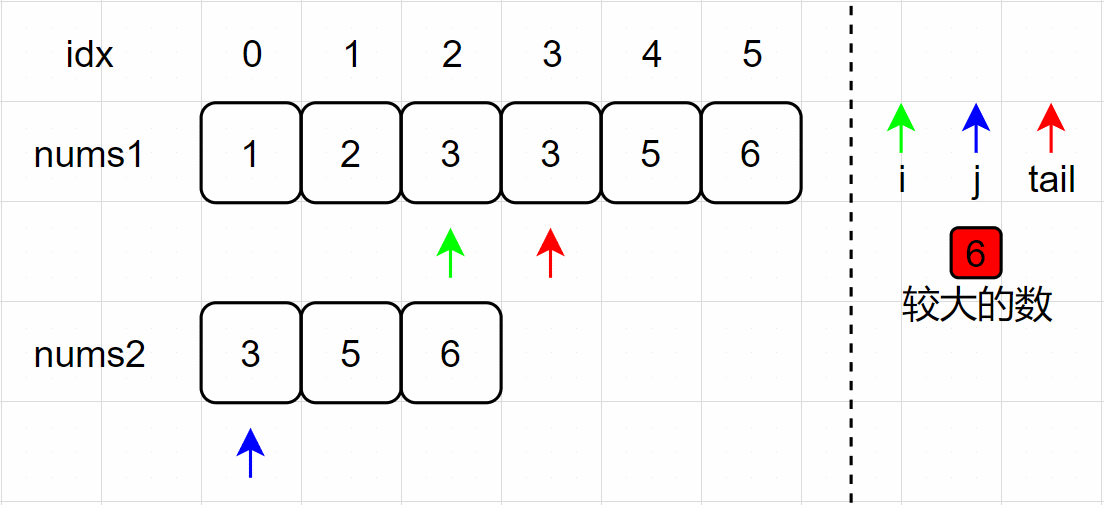
(7)i、tail 指针分别左移一个单位,为下次比较做准备;
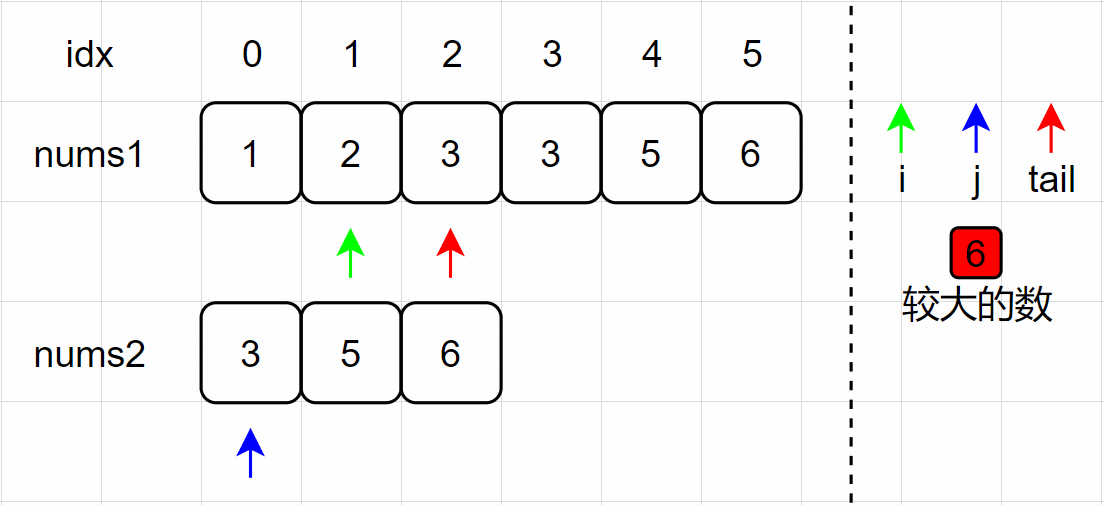
(8)nums1[1] < nums2[0] ,将较大的 nums2[0] 放置在 tail 处;
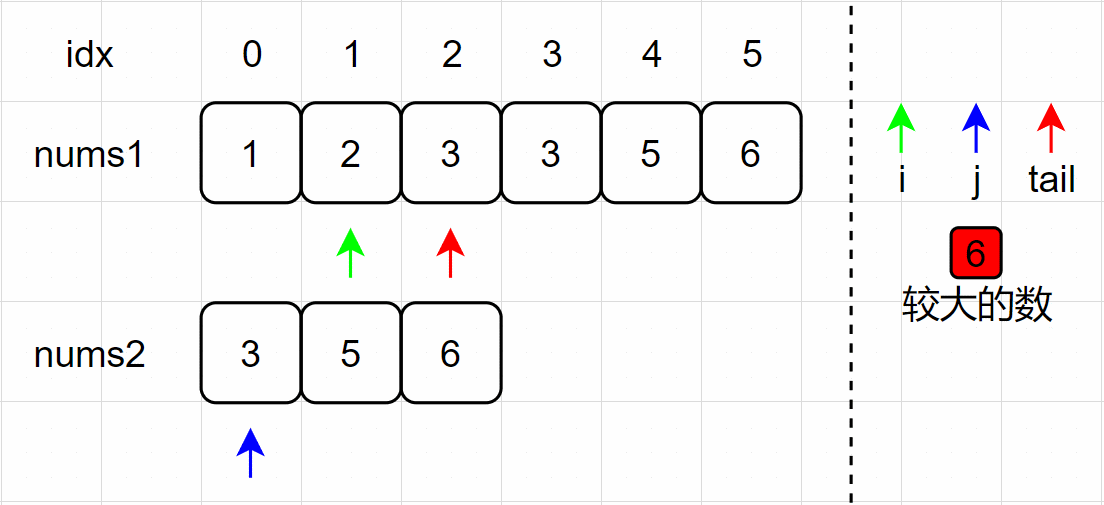
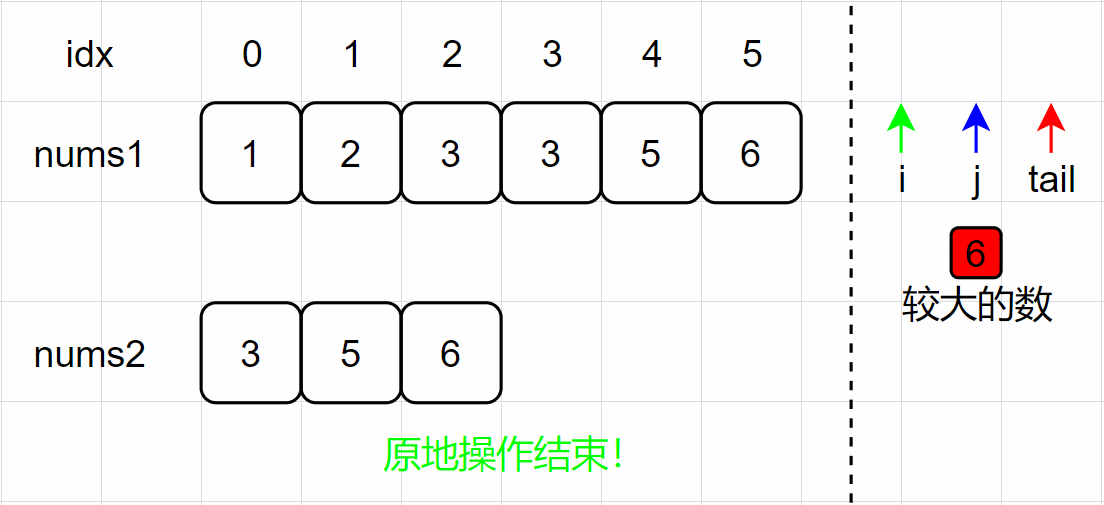
(9)j、tail 指针分别左移一个单位,j 指针越界,原地操作结束,数组 nums1 为最后合并后的数组。
实现代码
class Solution {
public:void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {int i = m - 1, j = n - 1, k = m + n - 1;while (i >= 0 && j >= 0) {if (nums2[j] > nums1[i]) {nums1[k--] = nums2[j--];}else {nums1[k--] = nums1[i--];}}while (j >= 0) {nums1[k--] = nums2[j--];}}
};
时间复杂度: O ( m + n ) O(m+n) O(m+n)。
空间复杂度: O ( 1 ) O(1) O(1),原地操作,仅仅使用了三个指针变量。
写在最后
如果文章内容有任何错误或者您对文章有任何疑问,欢迎私信博主或者在评论区指出 💬💬💬。
如果大家有更优的时间、空间复杂度方法,欢迎评论区交流。
最后,感谢您的阅读,如果感到有所收获的话可以给博主点一个 👍 哦。