一、插入排序(直接、折半、希尔)
【2009统考】若数据元素序列{11,12,13,7,8,9,23,4,5}是采用下列排序方法之一得到的第二趟排序后的结果,则该排序算法只能是(B)
A、冒泡排序 B、插入排序 C、选择排序 D、2路归并排序
解析:11、12、13、7、8、9、23、4、5
A、C都是一趟排序后必定有一个元素在最终位置上,2路归并排序经过第二趟排序后应该每四个有序
B是前n个有序
【2012统考】对同一待排序序列分别进行折半插入排序和直接插入排序,两者之间可能的不同之处是(D)
A、排序的总趟数 B、元素的移动次数
C、使用辅助空间的数量 D、元素之间的比较次数
解析:
折半插入:在寻找待插入位置时,使用折半查找。总趟数仍然是元素的个数,不同的元素之间比较的次数,折半插入排序 < 插入排序。
次数:折半,nlog2n;直接,n^2
【2014统考】用希尔排序对一个数据序列进行排序时,若第1趟排序结果为9,1,4,13,7,8,20,23,15,则该趟排序采用的增量可能是(B)
A、2 B、3 C、4 D、5
解析:
d1 = 3:
(a1,a4,a7) = (9,13,20),(a2,a5,a8) = (1,7,23),(a3,a6,a9) = (4,8,15),符合希尔排序
希尔排序,选择增量d,增量序列(i , i + d , i + 2d ……)中的元素进行排序
【2018统考】对初始数据序列(8,3,9,11,2,1,4,7,5,10,6)进行希尔排序。若第一趟排序结果为(1,3,7,5,2,6,4,9,11,10,8),第二趟排序结果为(1,2,6,4,3,7,5,8,11,10,9),则两趟排序采用的增量依次是(D)
A、3,1 B、3,2 C、5,2 D、5,3
解析:排除法
第一趟:"1"在第一个位置,证明"1"与第一个元素交换了位置,选项中增量只有3和5,若选择增量3则与8交换的是4,排除AB;
第二趟:"2"和"3"位置互换,若选择增量2则无法交换2、3,所以增量为3
二、交换排序(冒泡、快速)
【2010统考】采用递归方式对顺序表进行快速排序。下列关于递归次数的叙述中,正确的是(D)
A、递归次数与初始数据的排列次序无关
B、每次划分后,先处理较长的分区可减少递归次数
C、每次划分后,先处理较短的分区可减少递归次数
D、递归次数与每次划分后得到的分区的处理顺序无关
解析:
递归的次数只与各元素的初始排列有关。若每次划分的分区比较平衡,则递归次数少;若分区不平衡,递归次数多。与处理顺序无关
【2014统考】下列选项中,不可能是快速排序第2趟排序结果的是(C)
A、2,3,5,4,6,7,9 B、2,7,5,6,4,3,9 C、3,2,5,4,7,6,9 D、4,2,3,5,7,6,9
解析:
快排每次会有大于等于i个元素在最终位置上
2、3、4、5、6、7、9
C、 3、2、5、4、7、6、9 只有一个,所以不可能是第二趟排序的结果
【2016统考】已知由n(n = 2、3、……)个正整数构成的集合A = {ak|0 <= k < n },将其划分为两个不相交的子集A1和A2,元素个数分别是n1和n2,A1和A2中的元素之和分别为S1和S2.设计一个尽可能高效的划分算法,满足|n1-n2|最小且|S1-S2|最大。要求:
1)给出算法基本思想
2)根据设计思想,采用C或C++语言描述算法,关键之处给出注释
3)说明该算法的时间复杂度和空间复杂度
解析:
1)将最小的n/2个元素放在A1中,其余的元素放在A2中。
*i = n / 2,则分组完成
**i < n / 2,枢纽之前的所有元素均属于A1,继续对i之后对元素进行划分
***i > n / 2,枢纽之后对所有元素均属于A2,继续对i之前对元素进行划分
2)
int setPartition(int a[],int n)
{
int pivot,low=0,high=n-1,low0=0,high0=n-1,flag=1,k=n/2,i;
int s1=0,s2=0;
while(flag){pivot = a[low];while(low<high){while(low<high && a[high]>=pivot) high—-;if(low!=high) a[low] = a[high];while(low<high && a[low]<=pivot) low++;if(low!=high) a[high] = a[low];}
a[low] = pivot;
if(low == k-1) //枢纽是第n/2个小的元素flag=0;
else{if(low<k-1){ //小于一半,对右边划分low0 = ++low;high = high0;}else{ //大于一半,对左边划分high0 = —-high;low = low0;}}}for(i = 0; i < k ;i ++) s1+=a[i];for(i = k; i < n ;i ++) s2+=a[i];return s2-s1;
}三、选择排序
【2011统考】已知序列25,13,10,12,9是大根堆,在序列尾部插入新元素18,将其再调整为大根堆,调整过程中元素之间进行的比较次数是(B)
A、1 B、2 C、4 D、5
解析:堆——完全二叉树,一层满了才放下一层

【2015统考】已知小根堆为8,15,10,21,34,16,12,删除关键字8之后需重建堆,在此过程中,关键字比较次数(C)
A、1 B、2 C、3 D、4
解析:堆排序——完全二叉树
删除时将最后一个结点补到被删除的结点位置
所以16与10比较,不变;10与12比较,12向下移动;12与16比较,不变,总共比较3次
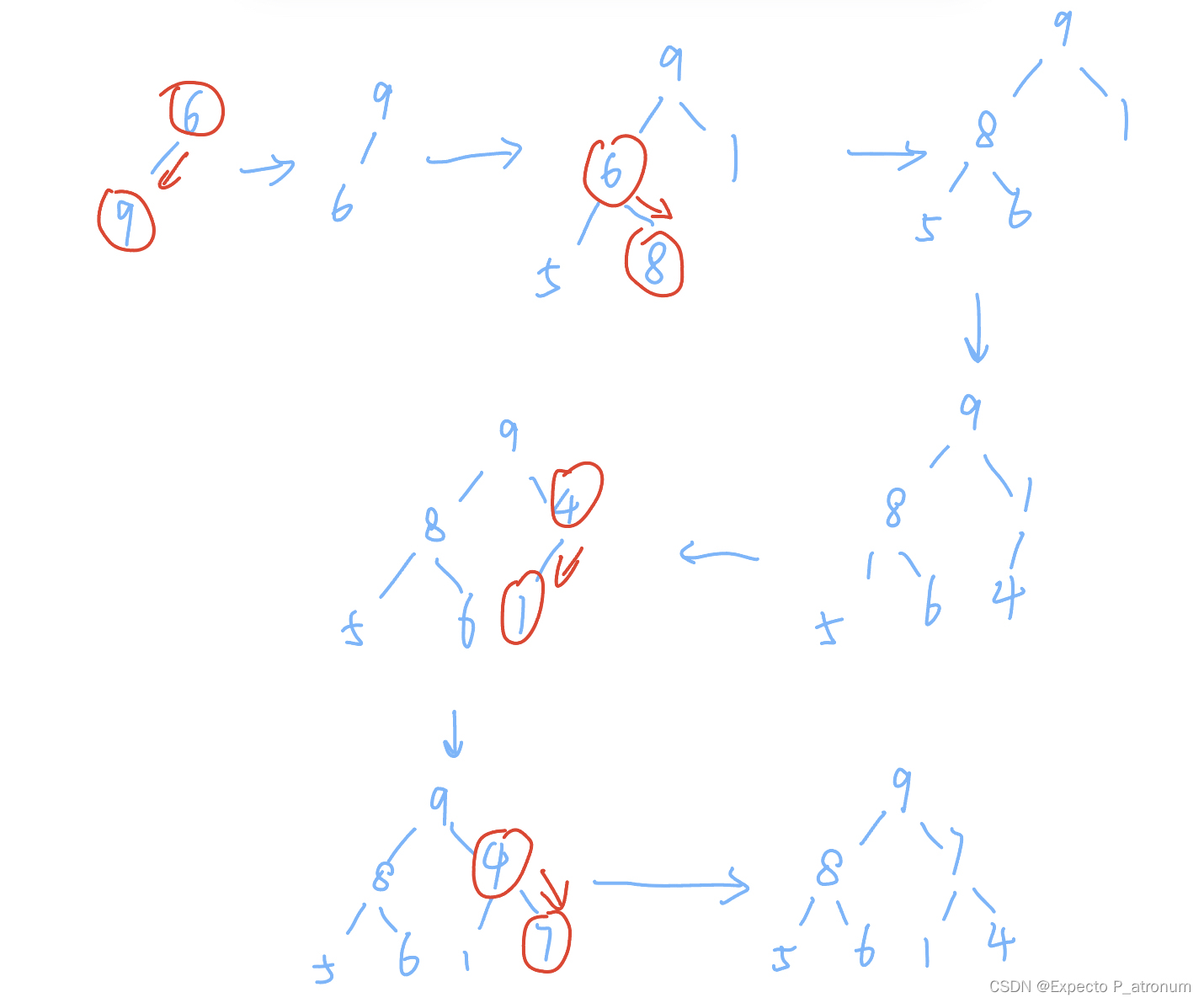
【2021统考】将关键字6,9,1,5,8,4,7依次插入到初始为空的大根堆H中,得到的H是(B)
A、9,8,7,6,5,4,1 B、9,8,7,5,6,1,4
C、9,8,7,5,6,4,1 D、9,6,7,5,8,4,1
解析:建堆方法:从出现不符合x根堆的结点开始,逐个往下比较,逐个交换。
【2022统考】现有n个数保存在一维数组M中,需要查找M中最小的10个数。请回答下列问题。
1)设计一个完成上述任务的算法,要求平均情况下的比较次数尽可能少,简述算法思想
2)说明算法的时间复杂度和空间复杂度
解析:
1)定义含10个元素的数组A,初始时元素值为该数组类型能表示的最大数MAX。遍历M中的每个元素s,如果s小于A[9],那么s覆盖A[9],再将A中元素重新排序。遍历结束后就得到10个最小的数。
2)O(1)、O(n)
四、归并排序和基数排序
【2017】在内部排序时,若选择了归并排序而未选择插入排序,则可能的理由是(B)
1、归并排序程序代码更短 2、归并排序占用空间更少 3、归并排序的运行效率更高
A、2 B、3 C、1、2 D、1、3
解析:
归并排序需要另开多一个数组空间复杂度为O(n),但时间复杂度比插入排序小O(nlog2n)
所以归并排序效率更高
【2021】设数组s[]={93,946,372,9,146,151,301,485,236,327,43,892},采用最低位优先(LSD)基数排序排列将S排列成升序序列。第一趟分配,收集后,元素372之前、之后紧邻的元素分别是(C)
A、43,892 B、236,301 C、301,892 D、485,301
解析:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 151、301 | 372、892 | 93、43 | 485 | 946、146、236 | 327 | 9 |
五、排序算法的比较
【2017】下列排序方法中,若将顺序存储更换为链式存储,则算法的时间效率会降低的是(D)
1、插入排序 2、选择排序 3、冒泡排序 4、希尔排序 5、堆排序
A、仅1、2 B、仅2、3 C、仅3、4 D、仅4、5
希尔排序和堆排序利用了顺序存储的随机访问性,若更换为链式存储,则破坏了随机访问性
【2020】对大部分元素已有序的数组排序时,直接插入排序比简单选择排序效率更高,其原因是(A)
1、直接插入排序过程中元素之间的比较次数更少
2、直接插入排序过程中所需的辅助空间更少
3、直接插入排序过程中元素的移动次数更少
A、仅1 B、仅3 C、仅1、2 D、1、2、3
解析:
简单选择排序的比较次序是固定的,n(n-1)/2次
直接插入排序的在基本有序时比较次数为n-1次
移动次数简单选择排序只需交换无序的位置,而直接插入排序需要移动无序位置后面的所有元素。
【2022】对数据进行排序时,若采用直接插入排序而不采用快速排序,则可能的原因是(D)
1、大部分元素已有序 2、待排序元素数量很少
3、要求空间复杂度为O(1) 4、要求排序算法是稳定的
A、仅1、2 B、仅3、4 C、仅1、2、4 D、1、2、3、4
1、快速排序不稳定
2、大部分元素有序并不适合快速排序,快速排序适合对称的序列
3、快速排序需要一个递归工作栈,空间复杂度为O(log2n),而快速排序空间复杂度为O(1)
不稳定算法:选择、希尔、快速、堆排序
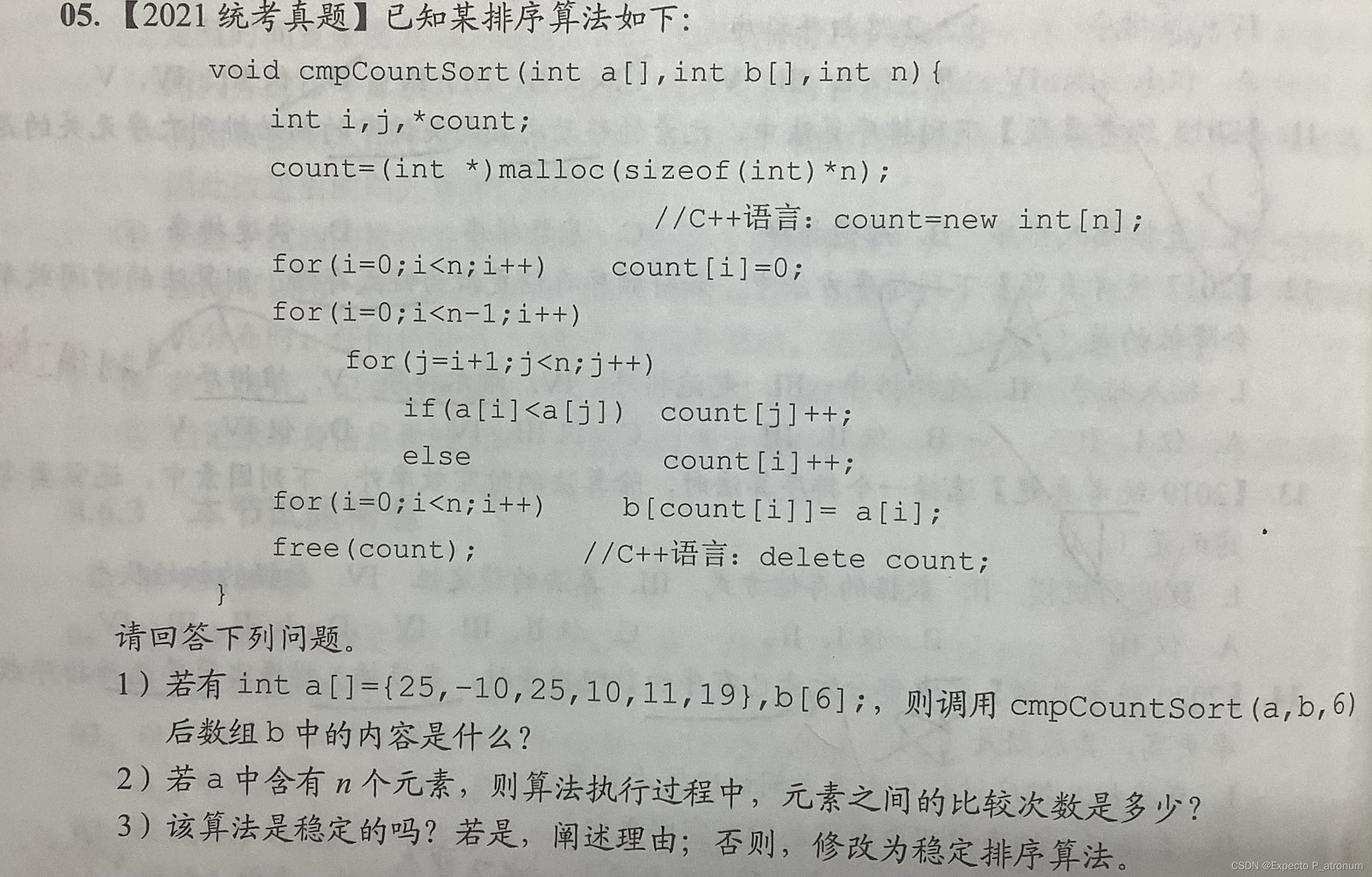
1)count = 4、0、5、1、2、3,所以b中保存的-10,10,11,19,25,25
2)1+2+3+4+……+n-1 = n(n-1)/2次
3)不稳定,将a[i] < a[j]改为,a[i]<=a[j]
六、外部排序
【2013】已知三叉树T中6个叶结点的权分别是2,3,4,5,6,7,T的带权(外部)路径长度最小的是(B)
A、27 B、46 C、54 D、56
6 % (3-1) = 1 需要添加一个虚段,
(2+3)*3+(4+5)*2 +(6+7) = 46
【2019】设外存有120个初始归并段,进行12路归并时,为实现最佳归并需要补充的虚段数是(B)
A、1 B、2 C、3 D、4
解析:只存在度为0和12 的点,n0 = (12-1) x + 1, n12 = (120 - 1 + x ) / (12-1)
因为n12为整数,所以x = 2