个人理解

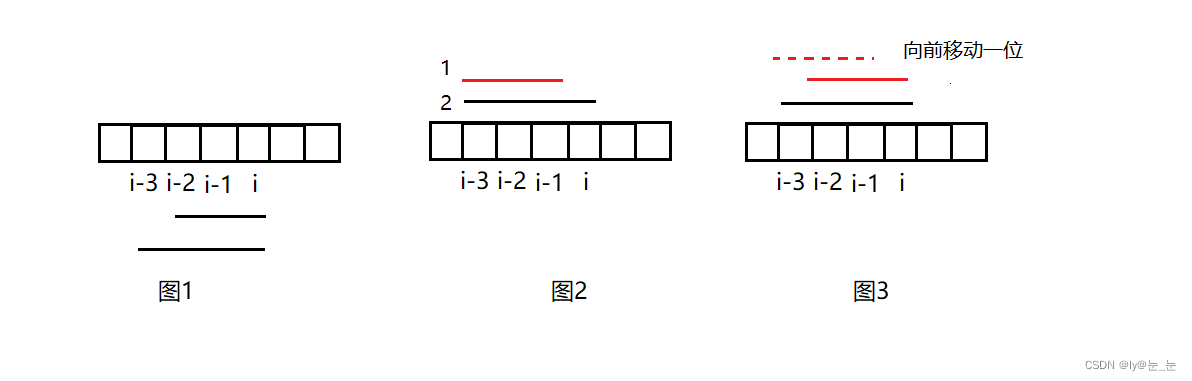
我理解的KMP 算法就是记录前缀与后缀，每当遇到不匹配的时候由于后缀已经被匹配过，所以下次应该跳到匹配过的后缀也就是相应的前缀后面在进行匹配。

如何计算前缀

参考卡哥网站 前缀计算

然后利用前缀表去做匹配

leetcode 28

class Solution {public int strStr(String haystack, String needle) {int[] next=new int[needle.length()];int j=0;next[0]=j;for(int i=1;i<needle.length();i++){//因为找相等的前缀所以遇到不等的就也跳前缀while(j>0&&needle.charAt(i)!=needle.charAt(j)){j=next[j-1];}if(needle.charAt(i)==needle.charAt(j)){j++;}next[i]=j;}int i=0;j=0;while(i<haystack.length()){//遇到不等的就跳前缀while(j>0 && haystack.charAt(i)!=needle.charAt(j)){j=next[j-1];}if(haystack.charAt(i)==needle.charAt(j)){j++;}if(j==needle.length()){return i-j+1;}i++;}return -1;}
}