前言

本文主要对PCA主成分分析中的数学原理进行介绍，将不涉及或很少涉及代码实现或应用，阅读前请确保已了解基本的机器学习相关知识。

文章概述

PCA主成分分析属于矩阵分解算法中的入门算法，通过分解特征矩阵来实现降维。

本文主要内容：

• 前置知识：包括样本方差、协方差、协方差矩阵、散度矩阵的简单介绍
• 特征值分解EVD和奇异值分解EVD的原理和流程
• 分别基于EVD和SVD的PCA实现方法
• PCA的应用以及对一些应用或说明的补充

前置知识

样本方差（Variance）：样本方差反映一组数据变异程度或分散程度大小的指标；计算公式:

Var=1N−1∑i=1N(xi−xˉ)2Var = \frac{1}{N-1}\sum^N_{i=1}(x_i-\bar{x})^2Var=N−11​i=1∑N​(xi​−xˉ)2

• NNN：某特征下的样本量
• xix_ixi​：某特征下的第 iii 个样本值
• xˉ\bar{x}xˉ：某特征下样本的均值

为什么分母为 N−1N-1N−1：这是在计算样本方差时对方差计算公式的一个修复，目的是得到总体方差的一个无偏估计，具体可参考下面文章中的"无偏估计与样本方差小节"：

• 【特征选择】Filter - 过滤法中的数学原理 - 掘金 (juejin.cn)

协方差（Covariance）：用来刻画两个随机变量 XXX，YYY之间的相关性；计算公式：

Cov(X,Y)=1N−1∑i=1N(xi−xˉ)(yi−yˉ)Cov(X,Y) = \frac{1}{N-1}\sum^N_{i=1}(x_i-\bar{x})(y_i-\bar{y})Cov(X,Y)=N−11​i=1∑N​(xi​−xˉ)(yi​−yˉ​)

• NNN：特征 X,YX, YX,Y 下的样本量
• xi,yix_i, y_ixi​,yi​：特征 X,YX,YX,Y 下的第 iii 个样本值
• xˉ,yˉ\bar{x},\bar{y}xˉ,yˉ​：特征 X,YX, YX,Y 下样本的均值

样本方差就是协方差的一种特殊形式，当两个变量相同时，协方差与样本方差相同。

如果两个变量的变化趋势一致，也就是说如果其中一个大于自身的期望值，另外一个也大于自身的期望值，那么两个变量之间的协方差就是正值，反之则为负值。

• 协方差为正或为负描述的是两组数据中的整体变化趋势相同或相反；协方差为正，则我们说两变量正相关，反之则为负相关。

协方差的绝对值越大，一定程度上两变量相关性越强

• 从公式上可以看出，若当 xix_ixi​ 大于 xˉ\bar{x}xˉ 时，yiy_iyi​ 总是大于或小于 yˉ\bar{y}yˉ​，则结果的绝对值是最大的（全为正数或全为负数然后累加），这种情况也就是变量 XXX 与变量 YYY 之间的变化趋势总是相同的，我们就认为这两个变量之间有着很强的相关性。

即协方差的正负表示两组数据的总体变化趋势，绝对值大小表示变化趋势符合程度。

协方差矩阵（Covariance Matrix）：一个大小为 N∗NN*NN∗N 的对称矩阵，且是半正定矩阵，由某组数据中的每对变量之间的协方差组成，正对角线上元素为各变量的方差。

例：某数据中含有三个变量（特征），分别为 X,Y,ZX,Y,ZX,Y,Z，则该数据的协方差矩阵为：

Σ=[Cov(X,X)Cov(X,Y)Cov(X,Z)Cov(Y,X)Cov(Y,Y)Cov(Y,Z)Cov(Z,X)Cov(Z,Y)Cov(Z,Z)]\Sigma = \begin{bmatrix} Cov(X, X) & Cov(X,Y) & Cov(X,Z) \\ Cov(Y,X) & Cov(Y,Y) & Cov(Y,Z) \\ Cov(Z,X) & Cov(Z,Y) & Cov(Z,Z) \end{bmatrix}Σ=⎣⎡​Cov(X,X)Cov(Y,X)Cov(Z,X)​Cov(X,Y)Cov(Y,Y)Cov(Z,Y)​Cov(X,Z)Cov(Y,Z)Cov(Z,Z)​⎦⎤​

不难看出，Cov(X,X)Cov(X,X)Cov(X,X) 其实就是变量 XXX 的方差，即正对角线上的三个元素分别为这三个变量本身的方差；由于 Cov(X,Y)=Cov(Y,X)Cov(X,Y) = Cov(Y,X)Cov(X,Y)=Cov(Y,X)，因此该矩阵为对称矩阵；共含有3个变量，因此该协方差矩阵的大小为 3∗33*33∗3。

散度矩阵：散度矩阵和协方差矩阵类似，有时计算散度矩阵，有时计算协方差矩阵，二者意义差不多，散度矩阵公式：

S=(n−1)[Cov(X,X)Cov(X,Y)Cov(X,Z)Cov(Y,X)Cov(Y,Y)Cov(Y,Z)Cov(Z,X)Cov(Z,Y)Cov(Z,Z)]S = (n-1) \begin{bmatrix} Cov(X, X) & Cov(X,Y) & Cov(X,Z) \\ Cov(Y,X) & Cov(Y,Y) & Cov(Y,Z) \\ Cov(Z,X) & Cov(Z,Y) & Cov(Z,Z) \end{bmatrix}S=(n−1)⎣⎡​Cov(X,X)Cov(Y,X)Cov(Z,X)​Cov(X,Y)Cov(Y,Y)Cov(Z,Y)​Cov(X,Z)Cov(Y,Z)Cov(Z,Z)​⎦⎤​

从公式也可以看出，散度矩阵其实就是协方差矩阵乘以 n−1n-1n−1，不难看出两矩阵的特征值是相同的。

特征值分解与奇异值分解

EVD：特征值分解

对于矩阵 AAA，有一组特征向量 VVV，将这组向量进行正交化、单位化，就能得到一组正交单位向量。特征值分解，就是将矩阵 AAA 分解为如下式：

A=QΛQ−1A=Q\Lambda Q^{-1}A=QΛQ−1

• AAA：nnn 阶方阵
• QQQ：由矩阵 AAA 对应的特征向量组成的矩阵
• Λ\LambdaΛ：对角阵，正对角线上各元素由矩阵 AAA 对应的特征向量组成，其中按特征值大小进行依次排列

线性代数中相似矩阵的定义：设 A,BA,BA,B 是 nnn 阶方阵，若存在可逆矩阵 PPP，使得 B=P−1APB=P^{-1}APB=P−1AP，则称矩阵 AAA 与 BBB 相似，P−1APP^{-1}APP−1AP 是对 AAA 做相似变换。

参考相似矩阵的定义，左乘 PPP 右乘 P−1P^{-1}P−1 和左乘 P−1P^{-1}P−1 右乘 PPP 只是参考矩阵 AAA 和 BBB 的角度不同，例如在 B=P−1APB= P^{-1}APB=P−1AP 中两边分别左乘一个矩阵 PPP 右乘一个矩阵 P−1P^{-1}P−1 后可以得到 A=PBP−1A=PBP^{-1}A=PBP−1。

在特征值分解中，不难看出其本质就是矩阵 AAA 与对角阵 Λ\LambdaΛ 相似，也就是 矩阵AAA 可相似对角化，Λ\LambdaΛ 为矩阵 AAA 的相似标准型，A=QΛQ−1A=Q\Lambda Q^{-1}A=QΛQ−1，其中对角阵中各元素为矩阵 AAA 对应的特征值，特征值对应的特征向量组成矩阵 QQQ，即特征值分解其实就是矩阵 AAA 的相似对角化。

特征值分解基本流程：已知 nnn 阶方阵 AAA，有以下式子：

Ax=λx→(A−λE)X=0→∣A−λE∣=0Ax=\lambda x \rightarrow (A-\lambda E)X=0 \rightarrow |A-\lambda E|=0Ax=λx→(A−λE)X=0→∣A−λE∣=0

以此求出方阵 AAA 的特征值，然后将各个特征值代入到原式 ∣A−λE∣|A-\lambda E|∣A−λE∣ 中求出各特征向量，以特征值和特征向量得到 A=QΛQ−1A=Q\Lambda Q^{-1}A=QΛQ−1 中矩阵 QQQ 和对角阵 Λ\LambdaΛ。

一个高维矩阵本质上就是高维空间中的一个线性变换，该矩阵的各特征值反映该矩阵各个方向变换的程度，我们取从大到小特征值中的前 mmm 个特征值，也就是提取了该矩阵变化程度最大的 mmm 个方向，其它方向进行舍弃，也就提取了该矩阵中最重要的 mmm 个特征，以此来近似原矩阵的线性变换。

特征值分解的局限性：特征值分解公式中的矩阵 AAA 为 nnn 阶方阵，但是在绝大多数情况下数据集中的特征和样本数都是不同的，特征值分解无法应用于这种情况。

SVD：奇异值分解

相比特征值分解，奇异值分解可以适用于任意形状的矩阵，公式如下：

A=UΣVTA=U\Sigma V^TA=UΣVT

• AAA：形状为 m∗nm*nm∗n 的矩阵
• UUU：形状为 m∗mm*mm∗m 的正交矩阵，其中的各向量被称为左奇异向量；该矩阵也被称为左奇异矩阵
• Σ\SigmaΣ：形状为 m∗nm*nm∗n 的矩阵，该矩阵除了正对角线以外其它位置的元素均为0，正对角线上的元素被称为奇异值；该矩阵也被称为对角奇异矩阵
• VVV：形状为 n∗nn*nn∗n 的正交矩阵，其中的各向量被称为右奇异向量；该矩阵也被称为右奇异矩阵

奇异值的数量：通过对角奇异矩阵的形状为 m∗nm*nm∗n 可以发现奇异值的数量为 min(m,n)min(m,n)min(m,n)

基于特征值分解的局限性，我们引入奇异值分解，奇异值分解的思路与其大同小异，假设有形状为 m∗nm*nm∗n 的矩阵 AAA，则有形状为 n∗nn*nn∗n 的方阵 ATAA^TAATA 和 形状为 m∗mm*mm∗m 的方阵 AATAA^TAAT

基于与特征值分解中相同的求特征值的公式，有：

(ATA)vi=λvi→(ATA−λE)vi=0→∣ATA−λE∣=0(AAT)ui=λui→(AAT−λE)ui=0→∣AAT−λE∣=0(A^TA)v_i = \lambda v_i \rightarrow (A^TA - \lambda E)v_i = 0 \rightarrow |A^TA - \lambda E| = 0 \\ (AA^T)u_i = \lambda u_i \rightarrow (AA^T - \lambda E)u_i = 0 \rightarrow |AA^T - \lambda E| = 0 \\(ATA)vi​=λvi​→(ATA−λE)vi​=0→∣ATA−λE∣=0(AAT)ui​=λui​→(AAT−λE)ui​=0→∣AAT−λE∣=0

分别求出方阵 ATAA^TAATA 和 方阵 AATAA^TAAT 的各特征值和特征向量后，由于：

ATA=(UΣVT)T(UΣVT)=VΣTUTUΣVT=VΣ2VT=VΣ2V−1AAT=(UΣVT)(UΣVT)T=UΣVTVΣTUT=UΣ2UT=UΣ2U−1A^TA = (U\Sigma V^T)^T(U\Sigma V^T) = V\Sigma^T U^T U \Sigma V^T = V\Sigma^2 V^T = V\Sigma^2 V^{-1} \\ AA^T = (U\Sigma V^T)(U\Sigma V^T)^T = U \Sigma V^T V\Sigma^T U^T = U\Sigma^2 U^T = U\Sigma^2 U^{-1}ATA=(UΣVT)T(UΣVT)=VΣTUTUΣVT=VΣ2VT=VΣ2V−1AAT=(UΣVT)(UΣVT)T=UΣVTVΣTUT=UΣ2UT=UΣ2U−1

• 性质一：Σ\SigmaΣ 为对称矩阵，对于对称矩阵有 ΣTΣ=Σ2\Sigma^T \Sigma = \Sigma^2ΣTΣ=Σ2
• 性质二：V,UV,UV,U 为正交矩阵，对于正交矩阵有 VTV=E(单位阵)V^T V = E(单位阵)VTV=E(单位阵)，VT=V−1V^T=V^{-1}VT=V−1

从中我们可以看出方阵 ATAA^TAATA 的各个特征向量组成矩阵 UUU，而方阵 AATAA^TAAT 的各个特征向量组成矩阵 VVV，矩阵 U,VU,VU,V 中的各特征向量又被分别称为左奇异向量和右奇异向量。

奇异值求解的思路有两种，第一种方法为：

A=UΣVT→AV=UΣVTV→AV=UΣ→Avi=σiui→σi=AviuiA=U\Sigma V^T \rightarrow AV = U\Sigma V^T V \rightarrow AV = U\Sigma \rightarrow Av_i = \sigma_i u_i \rightarrow \sigma_i = \frac{Av_i}{u_i}A=UΣVT→AV=UΣVTV→AV=UΣ→Avi​=σi​ui​→σi​=ui​Avi​​

• 这里的除法为对应位置元素相除

AV=UΣ→Avi=σiuiAV=U\Sigma \rightarrow Av_i = \sigma_i u_iAV=UΣ→Avi​=σi​ui​，展开这个矩阵方程可得：

AV=UΣ→A[v1⋯vn]=[u1⋯um][σ1σ2⋯]→Avi=σiuiAV=U\Sigma \rightarrow A\begin{bmatrix} v_1 \cdots v_n \end{bmatrix} = \begin{bmatrix}u_1 \\ \cdots \\ u_m\end{bmatrix} \begin{bmatrix} \sigma_1 & & \\ & \sigma_2 & \\ & & \cdots \end{bmatrix} \rightarrow Av_i=\sigma_iu_iAV=UΣ→A[v1​⋯vn​​]=⎣⎡​u1​⋯um​​⎦⎤​⎣⎡​σ1​​σ2​​⋯​⎦⎤​→Avi​=σi​ui​

• viv_ivi​：第 iii 个右奇异向量
• uiu_iui​：第 iii 个左奇异向量

由于我们上面方阵 ATAA^TAATA 和 AATAA^TAAT 的展开式中的对角奇异矩阵为 Σ2\Sigma^2Σ2，因此易得第二种方法：

σi=λi\sigma_i = \sqrt{\lambda_i}σi​=λi​​

• 这里的 λi\lambda_iλi​ 为第 iii 个特征值
• 方阵 AATAA^TAAT 和 ATAA^TAATA 的各特征值相同，但特征值对应的特征向量不同，即左奇异向量和右奇异向量不同

在矩阵 Σ\SigmaΣ 中各奇异值一般也是从大到小排列的。

通过SVD的过程我们可以看出，奇异值分解相当于将特征值分解将方阵拓展到了任意形状的矩阵，最终选择前 kkk 个最大的奇异值即可。

PCA基本原理

特征降维的目的：减少特征的数量的同时，又保留大部分有效信息。

• 将带有重复信息的特征进行合并，删除无效特征等，创造出能够代表原特征矩阵大部分信息的特征更少的新特征矩阵

PCA的本质就是在特征空间中通过某种线性变换将某些特征进行合并，合并后的新特征保留原来特征的大部分信息，即拥有最大的方差，被合并的特征在经过这种变换后方差很小，因此不再能提供有效信息，我们将其舍弃（被丢弃的特征向量被认为信息量很少， 这些信息很可能就是噪音），从而实现特征降维；此外，保留合并的新特征被称为 "主成分"。

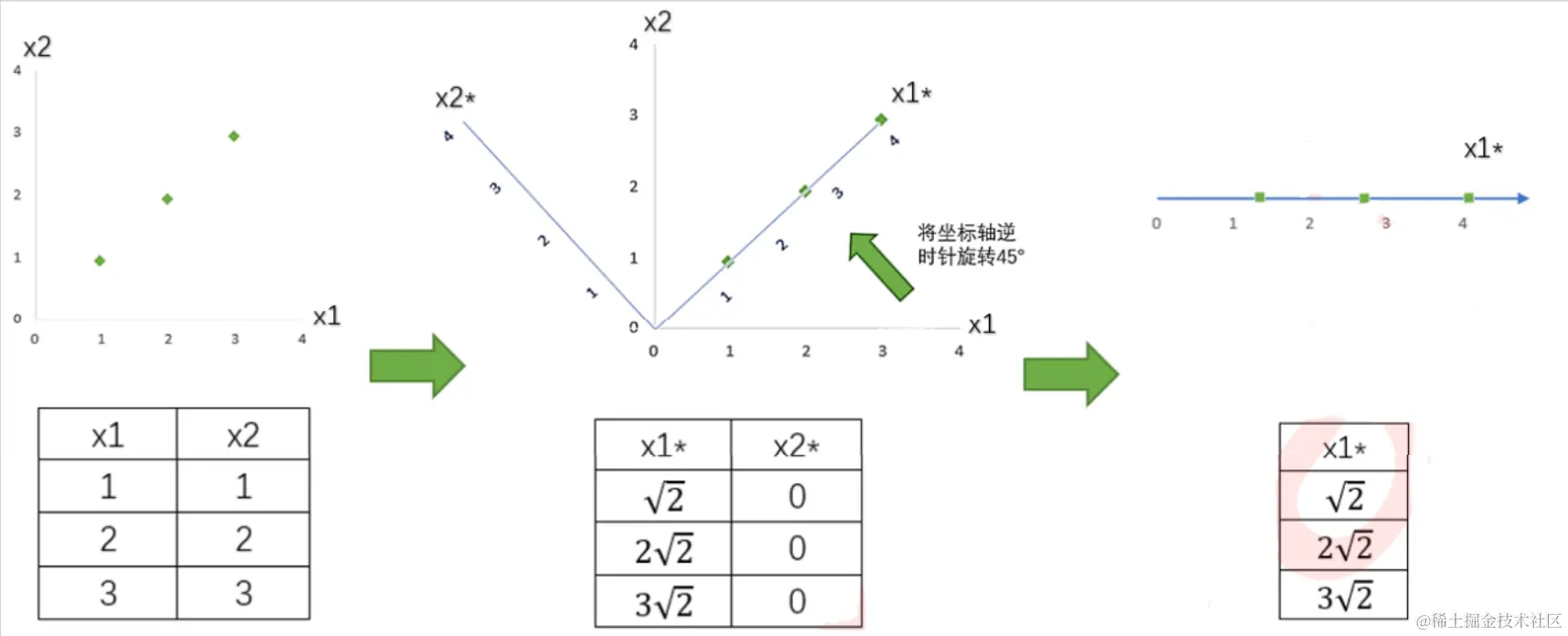
如图所示，图中通过旋转坐标轴将特征 x1x_1x1​ 与 x2x_2x2​ 合并为 x1∗x_1^*x1∗​，通过观察可以看出原始特征 x1x_1x1​ 和 x2x_2x2​ 的方差都为 23\frac{2}{3}32​，变换处理后的特征 x1∗x_1^*x1∗​ 和 x2∗x_2^*x2∗​ 的方差分别为 43\frac{4}{3}34​ 和 000，此时 x2∗x_2^*x2∗​ 的方差过小，我们不认为该特征能有效地提供信息，因此舍去，保留 x1∗x_1^*x1∗​。

此案例数据比较完美，也就是合并后 x2∗x_2^*x2∗​ 的方差为0，x1∗x_1^*x1∗​ 的方差等于原始特征 x1x_1x1​ 和 x2x_2x2​ 的方差之和，这里PCA认为保留了原来100%的信息，具体方法下方会详细介绍。

PCA主成分分析分别基于特征值分解和奇异值分解，因此一般有两种实现方法

PCA的两种实现方法

基于特征值分解：假设数据集 X=[x1x2⋯xn]X=\begin{bmatrix}x_1 & x_2 & \cdots & x_n \end{bmatrix}X=[x1​​x2​​⋯​xn​​]，共 nnn 个特征，需要降至 kkk 维，一般流程如下：

1. 去中心化处理，即每个特征下的各个样本值减去各自均值
2. 计算协方差矩阵，即 1nXXT\frac{1}{n}XX^Tn1​XXT
3. 基于特征值分解方法求协方差矩阵 1nXXT\frac{1}{n}XX^Tn1​XXT 的特征值和特征向量（这里除不除以 1n\frac{1}{n}n1​ 对结果没有影响）
4. 对特征值从大到小排序，选择其中最大的 kkk 个特征值
5. 将选中的 kkk 个特征向量分别作为行向量组成新的特征向量矩阵 PPP
6. 将原数据映射新空间中，即 Y=PXY=PXY=PX，其中 YYY 为降维后的特征矩阵

对于使用的矩阵 1nXXT\frac{1}{n}XX^Tn1​XXT，XXTXX^TXXT 中的各元素为各特征之间的内积，也就是协方差信息，保存了各个向量之间的协方差（相关性）和每个向量本身的方差，每个向量与其它向量的相关性组成的矩阵相当于对原来整个数据集中所有数据的一个压缩，当然这个过程也会损失一定程度的信息。

基于奇异值分解：假设数据集 X=[x1x2⋯xn]X=\begin{bmatrix}x_1 & x_2 & \cdots & x_n \end{bmatrix}X=[x1​​x2​​⋯​xn​​]，共 nnn 个特征，需要降至 kkk 维，一般流程如下：

1. 去中心化处理，即每个特征下的各个样本值减去各自均值
2. 计算协方差矩阵，即 1nXXT\frac{1}{n}XX^Tn1​XXT
3. 基于奇异值分解方法求协方差矩阵 1nXXT\frac{1}{n}XX^Tn1​XXT 的特征值和特征向量（这里除不除以 1n\frac{1}{n}n1​ 对结果没有影响）
4. 对右奇异矩阵从大到小排序，选择其中最大的 kkk 个特征值
5. 将选中的 kkk 个特征向量分别作为列向量组成新的特征向量矩阵 PPP
6. 将原数据映射新空间中，即 Y=PTXY=P^TXY=PTX，其中 YYY 为降维后的特征矩阵

在基于奇异值分解的PCA中，左奇异矩阵用于压缩行，而右奇异矩阵用于压缩列（特征），即使用SVD分解协方差的PCA可以实现两个方向的降维。

相比基于EVD的PCA，基于SVD的PCA的好处：一些SVD算法实现可以不求协方差矩阵 XXTXX^TXXT，直接求出右奇异矩阵，大大提高了计算效率，降低了时间成本

PCA的理论拓展

我们基于最大方差理论来进行介绍。

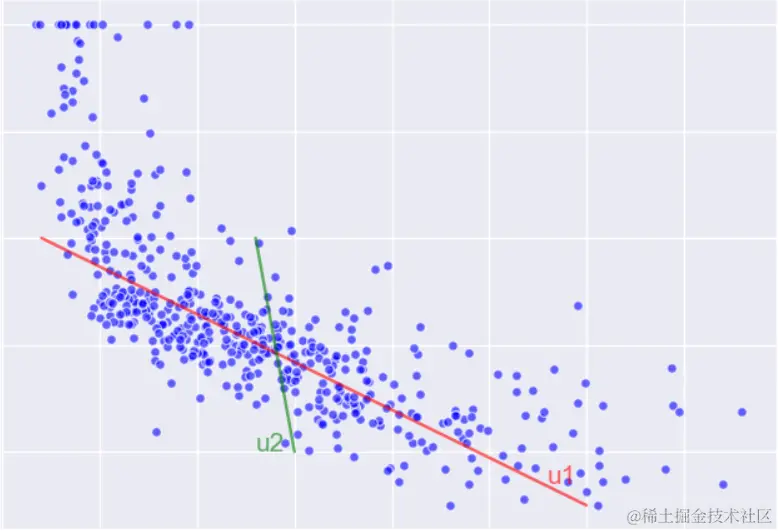
在信号处理中认为信号具有较大的方差，噪声有较小的方差，信噪比就是信号与噪声的方差比，越大越好。例如上图中样本在 u1u_1u1​（红线）方向上的投影方差较大，在 u2u_2u2​（绿线）方向上的投影方差较小，那么可认为 u2u_2u2​ 上的投影是由噪声引起的；因此认为特征的方差越大，对建模越有用，最好的 kkk 维特征是将 nnn 维样本数据降至 kkk 维后，每个特征的样本方差都很大。

假如说我要要从图中的 u1u_1u1​ 和 u2u_2u2​ 选一条来做投影，那按照最大方差理论肯定是选 u1u_1u1​ 更好。

PCA使用的信息量衡量指标：样本方差，又称可解释性方差；一定程度上，某特征的方差越大，说明样本区分度越高，提供的信息越多；在PCA中，认为方差越大则特征所能表达的信息就越多。

重建原始数据：例如将原始的 nnn 维数据降维至 kkk 维数据，我们降维的公式为 Y=PTXY=P^TXY=PTX，等式两边同时左乘矩阵 PPP，得到逆转公式：

Xapprox=PYX_{approx}=PYXapprox​=PY

• XapproxX_{approx}Xapprox​：逆转后得到的矩阵
• PPP：右奇异矩阵中由前 kkk 个特征值对应的特征向量作为列向量组成的矩阵
• YYY：降维后矩阵

平均平方映射误差(Average Squared Projection Error) ：原始数据 xix_ixi​ 和映射值 xapprox(i)x_{approx(i)}xapprox(i)​ 之间的差。即 xix_ixi​ 和其在低维表面上的映射点之间的距离的平方；描述两向量之间的相关性。

ASPE=1N∑i=1N∣∣xi−xapprox(i)∣∣2ASPE = \frac{1}{N}\sum^{N}_{i=1}||x_i - x_{approx(i)}||^2ASPE=N1​i=1∑N​∣∣xi​−xapprox(i)​∣∣2

数据的总方差 (Total Variation) ：这些样本向量 xix_ixi​ 与本身的内积（方差）的均值；描述数据本身的整体变异程度（平均来看，我的训练样本距离零向量多远）。

Var=1N∑i=1N∣∣xi∣∣2Var = \frac{1}{N}\sum^N_{i=1}||x_i||^2Var=N1​i=1∑N​∣∣xi​∣∣2

PCA所做的事是尽可能最小化平均平方映射误差，对于降至目标维度 kkk，超参数 kkk 的选择可以依据下方的经验法则：

平均平方映射误差数据的总方差=1N∑i=1N∣∣xi−xapprox(i)∣∣21N∑i=1N∣∣xi∣∣2≤0.01\frac{平均平方映射误差}{数据的总方差}=\frac{\frac{1}{N}\sum^{N}_{i=1}||x_i - x_{approx(i)}||^2}{\frac{1}{N}\sum^N_{i=1}||x_i||^2} \le 0.01数据的总方差平均平方映射误差​=N1​∑i=1N​∣∣xi​∣∣2N1​∑i=1N​∣∣xi​−xapprox(i)​∣∣2​≤0.01

数据的总方差越大越好，平均平方映射误差越小越好，其比值越小越好，我们一般用以下式子：

∑i=1kSii∑i=1NSii≥0.99\frac{\sum_{i=1}^k S_{ii}}{\sum_{i=1}^N S_{ii}} \ge 0.99∑i=1N​Sii​∑i=1k​Sii​​≥0.99

即协方差矩阵中选择的 kkk 个特征值对应的特征向量的方差之和与原来全部特征向量的总方差的比值，若结果大于0.99，我们则认为降维后的矩阵保留了原来矩阵99%以上的信息。

补充说明

① 运算复杂：现在的编程语言在大型矩阵的运算上都不是很擅长，因此PCA往往需要占用很大的算力资源，计算较为缓慢。

② 主成分不具有可解释性：PCA是将原始特征进行压缩，降维后得到的主成分与原始特征不同，是通过某种变换组合起来的新特征。通常来说，在新的特征矩阵生成之前，我们不知道PCA建立了哪些新特征向量，新特征矩阵生成之后也不具有可读性。因此PCA一般不适用于探索特征和标签之间的关系的模型（如线性回归），因为无法解释的新特征和标签之间的关系不具有意义。

③ 基于SVD的PCA算法的优点：使用基于SVD的PCA算法可以跳过计算协方差矩阵这一步而直接得到右奇异矩阵，因此会大大减小计算量和时间成本。

④ 图像处理中的右奇异矩阵：对于右奇异矩阵以及PCA的逆转公式，在处理图像时，我们在计算得到右奇异矩阵后，选择前 kkk 个特征值对应的特征向量组成新矩阵 V(k,n)V_{(k,n)}V(k,n)​，当处理纯数值时，我们无法观察该矩阵的含义，但是若我们处理的是图像，由前 kkk 个特征值对应的特征向量组成的该矩阵表示的就是从原图像中提取的压缩后的主要信息，我们则可以通过可视化该空间矩阵，并将可视化结果与原图像进行对比以查看PCA主要从原图像中提取哪些信息。

⑤ 噪音过滤：PCA的逆转公式并不能真正完全将降维后的数据映射成和原来一模一样的特征矩阵，因为原来的信息在合并时就已经丢失了，降维并不是完全可逆的，可逆转是因为采用某种策略或算法基于降维后的数据对原来数据的预测；此外，降维的目的之一就是希望抛弃掉对模型带来负面影响的特征，带有效信息的特征的方差应该是远大于噪音的，所以相比噪音，有效的特征所带的信息应该不会在PCA过程中被大量抛弃，PCA的逆转能够在不恢复原始数据的情况下，将降维后的数据返回到原本的高维空间，因此这很容易联想到PCA的另一个应用-----降噪，利用这个性质我们可以实现数据噪音的过滤。