【MATLAB第74期】#源码分享 | 基于MATLAB的ARX-ARMAX线性自回归移动平均外生模型（结合最小二乘思路）

根据ARX预测输出和实际输出的误差向量，采用ARMAX算法结合ARX误差建模，对预测值进一步细化。通过将误差描述为白噪声的移动平均值，
目前，该代码仅支持输入维度为1，输出维度为1的数据。

一、ARX模型

1.ARX公式

其中，Y代表输出向量，u代表输入向量。
参数𝑎1,𝑎2,…,𝑎𝑝 , 𝑏0,𝑏1,…,𝑏𝑚 使用最小二乘算法求解。

上述方程可以写成矩阵形式：

2.ARX代码实现

clc;
clear all;
close all;
data=xlsread('数据.xlsx');
u_in=data(:,1);
y_out=data(:,2);
% ARX Process-----------------------------
L=length(u_in);
u_in_ID=u_in;%用于标识的输入数据
u_in_vfy=u_in;%用于验证的输入数据
y_out_ID=y_out;%用于标识的输出数据
y_out_vfy=y_out;%用于验证的输出数据
m=5;%用于生成输入、输出和错误的延迟顺序的参数
n=length(y_out_ID)-m;I=eye(n,1)+1;% 
I(1)=I(1)-1; % 53 *1   ones(53,1)
A=I;%初始化矩阵A    53*1
Y=y_out_ID((m+1):end);%定义Y矢量  ,输出延迟m个值
na=1;
%将输出延迟1到m-na放入A矩阵
for k=1:1:m-na  %m-1A=[A y_out_ID((m-k+1):(end-k))]; % 53*1 5:57  4:56  3:55  2:54输出
end%将“当前输入——第m个延迟输入”输入到矩阵A
for p=1:1:mk=p-1; %0 1 2 3 4A=[A u_in_ID((m-k+1):(end-k))]; % 53*1 6:58 5:57 4:56 3:55 2:54输入
end  % A  53*10
A(:,1)=[]; %删除用于初始化矩阵A的第一列
parsol=inv(A'*A)*A'*Y  %最小二乘法求解 %基于先前生成已识别输出（预测秒数）矢量输出、当前和以前的输入和参数通过最小二乘法求解
%平方法
n=length(y_out_vfy)-m;  %53
I=eye(n,1)+1;
I(1)=I(1)-1; 
A=I;
for k=1:1:m-naA=[A y_out_vfy((m-k+1):(end-k))];
endfor p=1:1:mk=p-1;A=[A u_in_vfy((m-k+1):(end-k))];
end
A(:,1)=[]; %删除用于初始化矩阵A的第一列
y_out_sysID=A*parsol;% 预测结果T_sim1 =y_out_sysID';
T_train=y_out_vfy((m+1):end)';
vfy=y_out_vfy((m+1):end);
M=size(T_sim1,2);%%  均方根误差
error1 = sqrt(sum((T_sim1 - T_train).^2) ./ M);%%  绘图
figure
plot(1: M, T_train, 'r-*', 1: M, T_sim1, 'b-o', 'LineWidth', 1)
legend('真实值', '预测值')
xlabel('预测样本')
ylabel('预测结果')
string = {'ARX训练集预测结果对比'; ['RMSE=' num2str(error1)]};
title(string)
xlim([1, M])
grid%%  相关指标计算
% R2
R1 = 1 - norm(T_train - T_sim1)^2 / norm(T_train - mean(T_train))^2;disp(['ARX训练集数据的R2为：', num2str(R1)])% MAE
mae1 = sum(abs(T_sim1 - T_train)) ./ M ;disp(['ARX训练集数据的MAE为：', num2str(mae1)])% MBE
mbe1 = sum(T_sim1 - T_train) ./ M ;disp(['ARX训练集数据的MBE为：', num2str(mbe1)])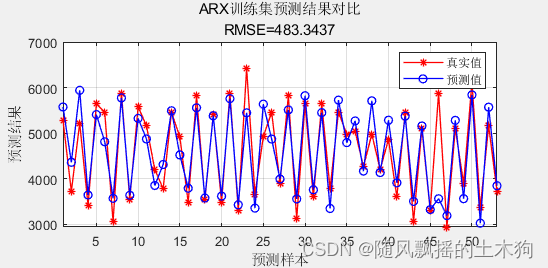

二、ARMAX模型

1.ARMAX公式

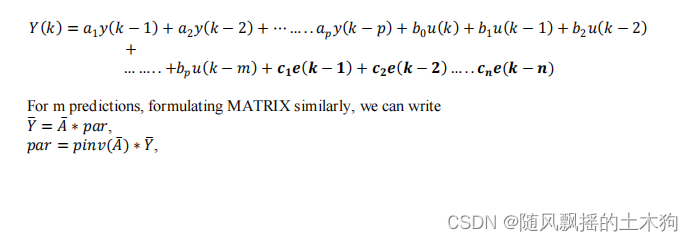
2.ARMAX代码实现（部分）

Y_actual=y_out_ID((m+1):end); %由于前m个值用于ARX中的延迟建模  53*1
u=u_in_ID((m+1):end);  %53*1 
Y_verify=y_out_vfy((m+1):end); %53*1
U_verify=u_in_vfy((m+1):end);%53*1
error =vfy- y_out_sysID;%误差矢量由实际错误组成
......
%基于先前生成已识别输出（预测秒数）矢量
%解决了输出、以前的错误、当前和以前的输入和参数
%通过最小二乘法
n=length(Y_verify)-m;
I=eye(n,1)+1;
I(1)=I(1)-1; %是一个哥伦布矢量，所有元素都是Unity
A=I;
Y=Y_verify((m+1):end);
for k=1:1:m-naA=[A Y_verify((m-k+1):(end-k))];
endfor p=1:1:mk=p-1;A=[A U_verify((m-k+1):(end-k))];
endfor p=1:1:mk=p;A=[A error((m-k+1):(end-k))];
end
A(:,1)=[];
Y_sysID=A*parsol;T_sim11 =Y_sysID';
T_train11=Y_verify((m+1):end)';
M11=size(T_sim11,2);%%  均方根误差
error11 = sqrt(sum((T_sim11 - T_train11).^2) ./ M11);%%  绘图
figure
plot(1: M11, T_train11, 'r-*', 1: M11, T_sim11, 'b-o', 'LineWidth', 1)
legend('真实值', '预测值')
xlabel('预测样本')
ylabel('预测结果')
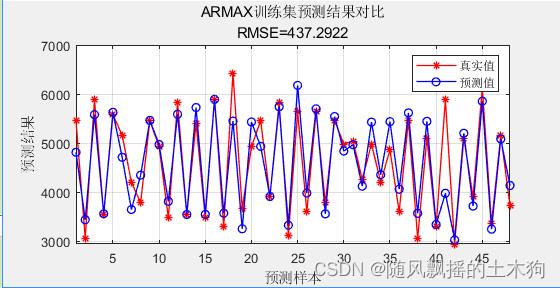
string = {'ARMAX训练集预测结果对比'; ['RMSE=' num2str(error11)]};
title(string)
xlim([1, M11])
grid%%  相关指标计算
% R2
R11 = 1 - norm(T_train11 - T_sim11)^2 / norm(T_train11 - mean(T_train11))^2;disp(['ARMAX训练集数据的R2为：', num2str(R11)])% MAE
mae11 = sum(abs(T_sim11 - T_train11)) ./ M11 ;disp(['ARMAX训练集数据的MAE为：', num2str(mae11)])% MBE
mbe11 = sum(T_sim11 - T_train11) ./ M11 ;

三、代码获取

CSDN后台私信“74期”即可获取下载方式。