3.4.1 采用递归算法解决问题 

3.4 栈与递归的关系

栈和递归之间有着紧密的关系，特别是在算法和程序设计中。栈作为一种数据结构，可以有效地支持递归算法的实现。本节我们将详细讨论栈在递归算法中的作用及其在程序设计中的重要性。

1. 递归算法的基本概念

• 定义和特点：
  • 递归是一种算法结构或编程技巧，其中函数直接或间接地调用自身来解决更小的问题实例。
  • 递归算法通常包含基本情况（终止条件）和递归步骤（自我调用来解决更小的问题）。

2. 栈在递归中的角色

• 概述：

  • 在实现递归时，栈被用作一个辅助数据结构，用于保存函数调用的信息，如返回地址和局部变量。
  • 栈的后进先出（LIFO）特性确保了函数调用的正确执行和返回。

• 详细描述：

  • 保存返回地址：在函数调用时，返回地址被推送到栈中，以便函数可以在执行完毕后返回到正确的位置。
  • 存储局部变量：函数的局部变量也存储在栈中，保证了在每次函数调用时，变量的正确初始化和使用。

3. 递归算法的设计和实现

• 基本步骤：

  • 确定基本情况：定义递归算法的终止条件。
  • 递归表达式：描述如何通过解决更小的问题来解决当前问题。

• 示例代码：

  #include <stdio.h>int factorial(int n) {if (n == 0) {return 1; // 基本情况，0的阶乘为1} else {return n * factorial(n - 1); // 递归表达式，n的阶乘是n乘以n-1的阶乘}
  }int main() {int number = 5;printf("The factorial of %d is %d\n", number, factorial(number));return 0;
  }
  

4. 栈和递归在程序设计中的应用

• 实例分析：
  • 在计算机科学中，栈和递归常用于解决各种问题，如数据结构操作（如树的遍历）、图形算法（如分治算法）和动态编程等。
  • 通过理解栈和递归的关系，程序员可以更好地设计和实现高效的算法。

注意事项

• 递归算法需要仔细设计基本情况和递归步骤，以避免无限递归和堆栈溢出错误。
• 递归虽然可以使代码更简洁和优雅，但也可能导致效率降低和内存使用增加，因此应谨慎使用。

 

 

3.4.2 递归的过程与递归工作栈 

3.4.2 递归过程与递归工作栈

在这段文本中，对递归过程和递归工作栈的概念和运行机制进行了详细阐述。现在我将帮你逐点分析这些内容：

递归函数的运行机制

1. 函数调用机制： 在程序中，函数可以调用其他函数，而递归则是函数调用自身。在函数调用中，调用函数和被调用函数的信息交换和链接是通过栈来实现的。

2. 函数调用和返回的过程：

   • 调用前需完成：
     1. 传递实参和返回地址给被调用函数。
     2. 为被调用函数的局部变量分配存储区。
     3. 控制转移到被调用函数。
   • 返回前需完成：
     1. 保存被调用函数的计算结果。
     2. 释放被调用函数的数据区。
     3. 根据保存的返回地址将控制转移到调用函数。

3. 递归函数的层次概念： 在递归函数中，每次调用都会形成一个新的层次。这些层次和调用的顺序密切相关，可以通过递归工作栈来保持跟踪。

递归工作栈

1. 递归工作栈的定义： 递归工作栈用于在递归过程中存储每一层递归所需的信息（如实参、局部变量和返回地址）。每次进入一个新的递归层次时，都会生成一个新的工作记录（或称活动记录）并压入栈顶。每次退出一个递归层次时，则从栈顶弹出一个工作记录。

2. 递归函数的运行示例： 以下是一个简化的阶乘函数递归调用过程的示例代码，解释了在递归过程中栈的运行情况和活动记录的使用：

   #include <stdio.h>long Fact(long n) {long temp;if (n <= 0) return 1;else {temp = n * Fact(n - 1);return temp;}
   }int main() {long n = 4;long result = Fact(n);printf("The factorial of %ld is: %ld\n", n, result);return 0;
   }
   

   解析：

   • main 函数调用 Fact(4)，进入第一层递归。
   • Fact(4) 调用 Fact(3)，进入第二层递归，这一过程继续，直到调用 Fact(0)，此时达到递归基条件，返回1。
   • 接着开始从栈顶逐步弹出每层递归的工作记录，计算并返回结果到上一层，直到最终返回到 main 函数。

结论

通过这段文本，我们可以更好地理解递归函数的运行机制和递归工作栈的工作原理。

 

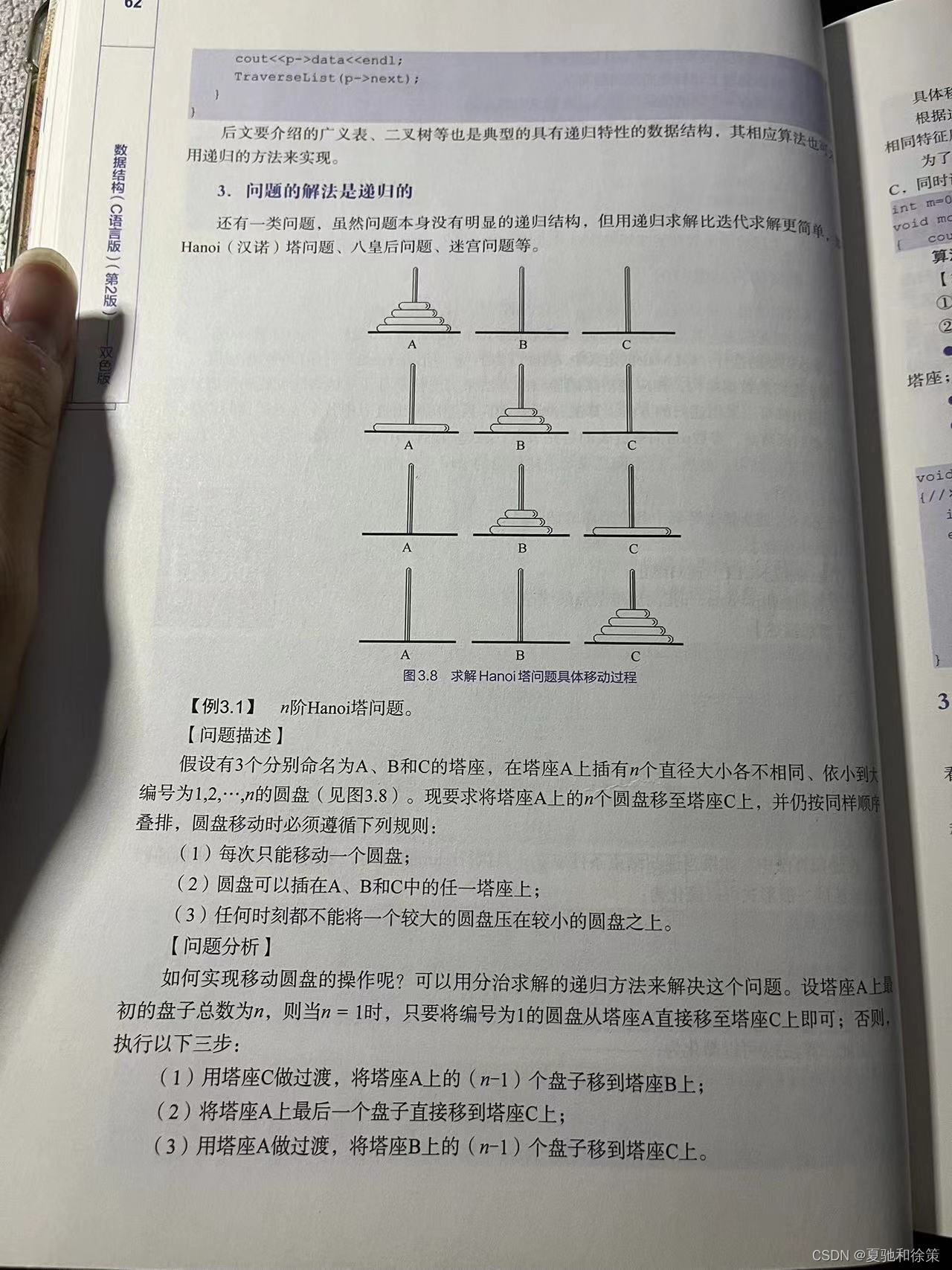
 3.4.3 递归算法的效率分析

这段文本对递归算法的效率进行了深入的分析，涉及时间复杂度和空间复杂度的计算。下面我会针对这些内容提供详细的解析：

### 3.4.3 递归算法的效率分析

#### 1. 时间复杂度的分析

在递归算法的分析中，时间复杂度通常通过建立递归方程来计算。递归方程的求解可以通过多种方法，其中一种是迭代法。迭代法通过将递归方程不断展开，最终将其转换为一个非递归的和式，然后估算这个和式来得到方程的解。

例如，我们可以使用迭代法来分析阶乘函数`Fact(n)`的时间复杂度：

int Fact(int n) {if (n == 0) return 1;else return n * Fact(n - 1);}

- **递归方程建立：**
  递归函数`Fact(n)`的执行时间可表示为`T(n)`，其中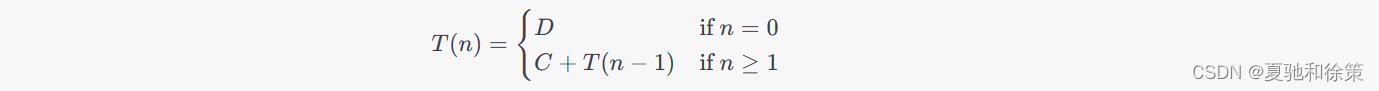

  其中D和C是常数，代表各个操作的执行时间。

- **递归方程解析：**
  通过迭代法我们可以将`T(n)`不断展开，直至找到一个模式或达到一个已知条件。按照文本的描述，我们可以得到`T(n) = nC + D`，因此时间复杂度为O(n)。

#### 2. 空间复杂度的分析

在递归算法中，系统使用“递归工作栈”来存储每层递归所需的信息，这是分析递归算法空间复杂度的关键。

- **递归工作栈的概念：**
  递归工作栈是用于存储每次递归调用所需的信息（如参数、局部变量和返回地址等）的数据结构。

- **空间复杂度计算：**
  对于递归算法，空间复杂度通常可以表示为

，其中是递归工作栈中工作记录数量与问题规模n的函数关系。例如，在阶乘问题、斐波那契数列问题和汉诺塔问题中，空间复杂度都是O(n)，因为工作栈中的记录数量与n成正比。

 

3.4.4 利用栈将递归转换为非递归的方法 

3.4.4 利用栈将递归转换为非递归的方法

在解析递归算法时，我们可以注意到它依赖于系统提供的隐式栈来执行。根据递归算法执行过程中的递归工作栈的状态变化，我们可以编写相应的非递归算法。以下是消除递归过程的具体步骤：

(1) 创建工作栈

创建一个工作栈来存储递归工作记录，包括实参（实际参数）、返回地址和局部变量等。

(2) 初始化非递归调用

在非递归调用的入口（被调用程序的开始处），初始化实参和返回地址。由于递归程序不能作为主程序，我们可以假设它最初是由某个调用程序调用的。

(3) 模拟递归分解过程

当不满足递归结束条件时，逐层递归，将实参、返回地址和局部变量压入栈中。这个过程可以通过循环语句来实现，从而模拟递归分解的过程。

(4) 设置递归退出条件

当递归结束条件被满足时，将给定常数作为当前函数值，标记递归的结束。

(5) 模拟递归求值过程

在栈不为空的情况下，重复执行以下步骤：弹出栈顶记录，根据记录中的返回地址执行特定的操作，即逐层计算当前函数值，直到栈为空为止。

结论

通过以上步骤，我们可以将任何递归算法转换为非递归算法。但是，这样改写后的非递归算法通常会失去原有的结构清晰度和可读性，有时还需进一步优化。更多具体实例可以参见本文后续的5和5.1节，其中包含二叉树中序遍历的非递归算法示例。