题目描述
这是 LeetCode 上的 「99. 恢复二叉搜索树」 ,难度为 「中等」。
Tag : 「二叉树」、「树的搜索」、「递归」、「迭代」、「中序遍历」、「Morris 遍历」
给你二叉搜索树的根节点 root,该树中的 恰好 两个节点的值被错误地交换。请在不改变其结构的情况下,恢复这棵树 。
示例 1: 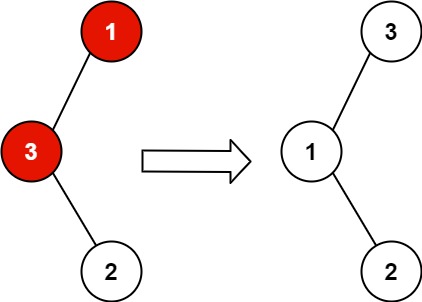
输入:root = [1,3,null,null,2]
输出:[3,1,null,null,2]
解释:3 不能是 1 的左孩子,因为 3 > 1 。交换 1 和 3 使二叉搜索树有效。
示例 2: 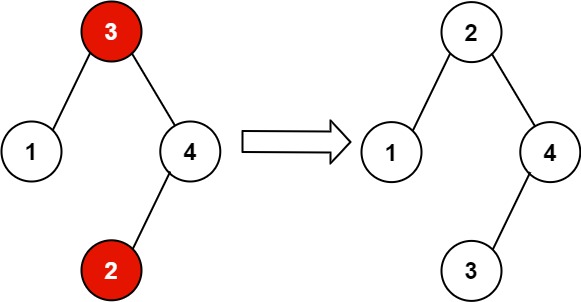
输入:root = [3,1,4,null,null,2]
输出:[2,1,4,null,null,3]
解释:2 不能在 3 的右子树中,因为 2 < 3 。交换 2 和 3 使二叉搜索树有效。
提示:
-
树上节点的数目在范围 内 -
进阶:使用 空间复杂度的解法很容易实现。你能想出一个只使用 空间的解决方案吗?
基本分析
首先,别想复杂了。
所谓的恢复二叉树(两节点互换),只需要将两节点的 val 进行互换即可,而不需要对节点本身进行互换。
中序遍历 - 递归 & 迭代
二叉搜索树,其中序遍历是有序的。
要找到哪两个节点被互换,可通过比对中序遍历序列来实现。
但将整个中序遍历序列保存下来,再检测序列有序性的做法,复杂度是 的(不要说题目要求的 ,连 都达不到)。
所以第一步,「这个「递归 & 迭代」的次优解,我们先考虑如何做到 的空间复杂度,即在中序遍历过程中找到互换节点」。
其实也很简单,除了使用 a 和 b 来记录互换节点,额外使用变量 last 来记录当前遍历过程中的前一节点即可:
若存在前一节点 last 存在,而且满足前一节点值大于当前节点(last.val > root.val),违反“有序性”,根据是否为首次出现该情况分情况讨论:
-
若是首次满足条件,即
a == null,此时上一节点last必然是两个互换节点之一,而当前root只能说是待定,因为有可能是last和root实现互换,也有可能是last和后续的某个节点实现互换。此时有
a = last, b = root -
若是非首次满足条件,即
a != null,此时当前节点root必然是两个互换节点中的另外一个。此时有
b = root
综上:如果整个中序遍历的序列中“逆序对”为一对,那么互换节点为该“逆序对”的两个成员;若“逆序对”数量为两对,则互换节点为「第一对“逆序对”的首个节点」和「第二对“逆序对”的第二个节点」。
Java 代码(递归):
class Solution {
TreeNode a = null, b = null, last = null;
public void recoverTree(TreeNode root) {
dfs(root);
int val = a.val;
a.val = b.val;
b.val = val;
}
void dfs(TreeNode root) {
if (root == null) return ;
dfs(root.left);
if (last != null && last.val > root.val) {
if (a == null) {
a = last; b = root;
} else {
b = root;
}
}
last = root;
dfs(root.right);
}
}
Java 代码(迭代):
class Solution {
public void recoverTree(TreeNode root) {
Deque<TreeNode> d = new ArrayDeque<>();
TreeNode a = null, b = null, last = null;
while (root != null || !d.isEmpty()) {
while (root != null) {
d.addLast(root);
root = root.left;
}
root = d.pollLast();
if (last != null && last.val > root.val) {
if (a == null) {
a = last; b = root;
} else {
b = root;
}
}
last = root;
root = root.right;
}
int val = a.val;
a.val = b.val;
b.val = val;
}
}
-
时间复杂度: -
空间复杂度: ,其中 为树高
中序遍历 - Morris 遍历
Morris 遍历也就是经常说到的“神级遍历”,其本质是通过做大常数来降低空间复杂度。
还是以二叉树的中序遍历为例,无论是递归或是迭代,为了在遍历完左节点(也可以是左子树)时,仍能回到父节点,我们需要使用数据结构栈,只不过在递归做法中是用函数调用充当栈,而在迭代做法则是显式栈。
「这使得空间复杂度为 ,而 Morris 遍历的核心则是利用“路径底部节点”中的空闲指针进行线索。」
举个 🌰,对于一棵最简单的二叉树:
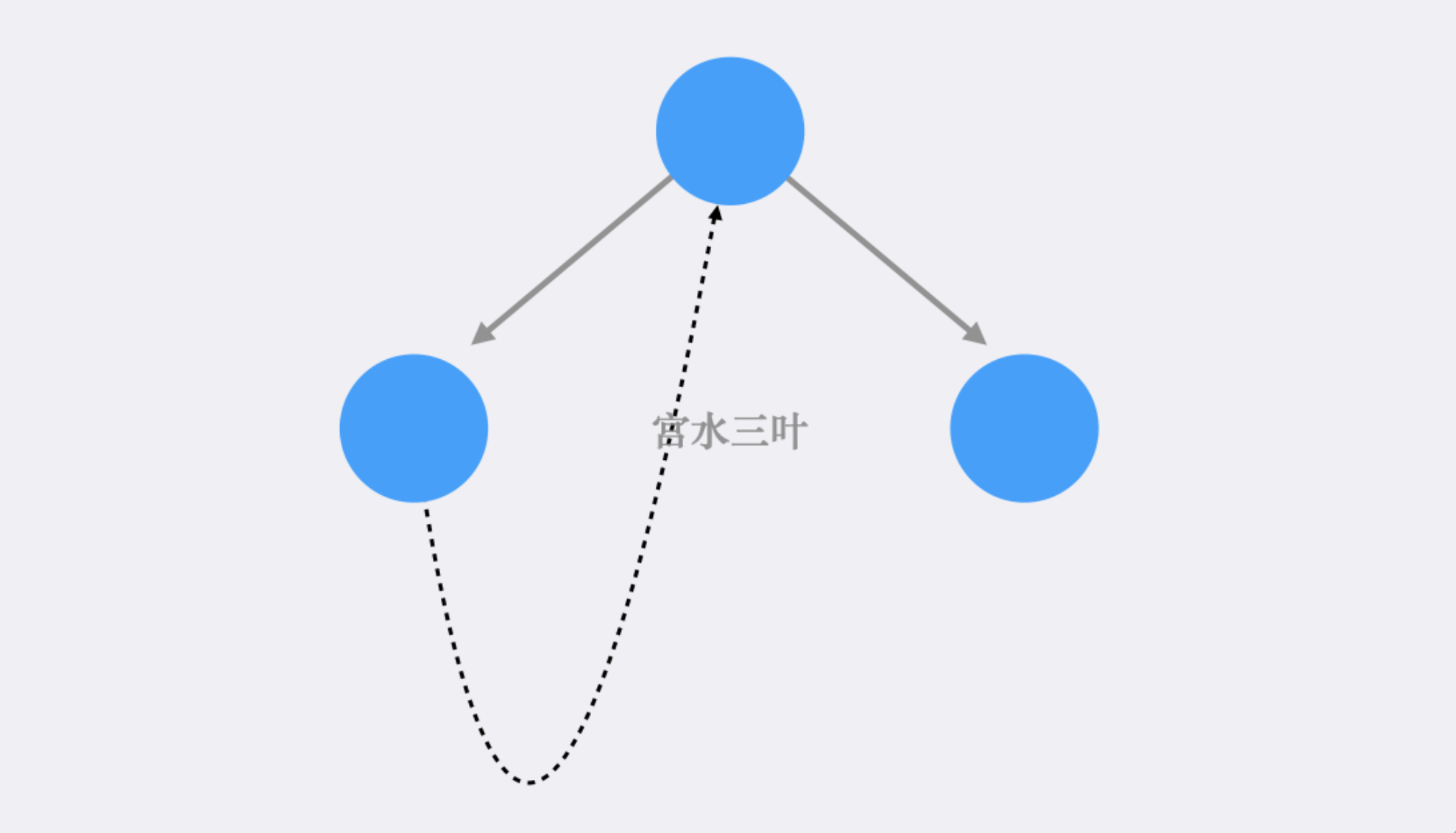
在中序遍历过程中,如果选择递归或迭代方式,并且不使用栈的情况,当遍历完左子节点(或左子树的最后一个节点)后,将会面临无法返回根节点的问题。
在 Morris 遍历中,从根节点开始,尚未真正遍历左子节点之前,就会先建立「左子节点(或左子树的最后一个节点)」与「当前根节点」之间的链接,从而避免使用栈。
具体的,Morris 遍历的中序遍历遵循如下流程(喜欢的话可以背过):
-
令根节点为当前节点
-
只要当前节点不为空(
while (root != null)),重复执行如下流程:-
若当前节点的左子节点为空(
root.left = null),将当前节点更新为其右子节点(root = root.right) -
若当前节点的左子节点不为空,利用临时变量
t存储,找到当前节点的前驱节点(左子树中最后一个节点):-
若前驱节点的右子节点为空(
t.right = null),将前驱节点的右子节点链接到当前节点(t.right = root),并将当前节点更新为左子节点(root = root.left) -
若前驱节点的右子节点不为空,说明已链接到当前节点,此时将前驱节点的右子节点置空(删除链接
t.right = null),遍历当前节点,并将当前节点更新为右子节点(root = root.right)
-
-
Java 代码:
class Solution {
public void recoverTree(TreeNode root) {
TreeNode a = null, b = null, last = null;
while (root != null) {
if (root.left == null) {
if (last != null && last.val > root.val) {
if (a == null) {
a = last; b = root;
} else {
b = root;
}
}
last = root;
root = root.right;
} else {
TreeNode t = root.left;
while (t.right != null && t.right != root) t = t.right;
if (t.right == null) { // 若前驱节点右子树为空, 说明是真正遍历左子树前, 建立与当前根节点的链接, 然后开始真正遍历左子树
t.right = root;
root = root.left;
} else { // 若已存在链接, 说明是第二次访问根节点, 左子树(前驱节点)已遍历完, 此时应该解开链接, 遍历当前节点以及右子树
t.right = null;
if (last != null && last.val > root.val) {
if (a == null) {
a = last; b = root;
} else {
b = root;
}
}
last = root;
root = root.right;
}
}
}
int val = a.val;
a.val = b.val;
b.val = val;
}
}
-
时间复杂度: -
空间复杂度:
最后
这是我们「刷穿 LeetCode」系列文章的第 No.99 篇,系列开始于 2021/01/01,截止于起始日 LeetCode 上共有 1916 道题目,部分是有锁题,我们将先把所有不带锁的题目刷完。
在这个系列文章里面,除了讲解解题思路以外,还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。
为了方便各位同学能够电脑上进行调试和提交代码,我建立了相关的仓库:https://github.com/SharingSource/LogicStack-LeetCode 。
在仓库地址里,你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。
更多更全更热门的「笔试/面试」相关资料可访问排版精美的 合集新基地 🎉🎉