当涉及到二元分类问题时，逻辑回归是一种常用的机器学习算法。它不仅简单而且有效，通常是入门机器学习领域的第一步。本文将介绍逻辑回归的基本概念、原理、应用场景和代码示例。

什么是逻辑回归？

逻辑回归是一种用于解决二元分类问题的统计学习方法。尽管其名称中包含"回归"一词，但实际上它是一种分类算法。逻辑回归的目标是预测输入变量与某个特定类别相关联的概率。

在逻辑回归中，我们使用一个称为Sigmoid函数的特殊函数来执行这种概率预测。Sigmoid函数的形状类似于"S"型曲线，它将输入的线性组合映射到0到1之间的概率值。

Sigmoid函数

Sigmoid函数的数学表达式如下：

其中，
$z$ 表示输入的线性组合。Sigmoid函数的输出范围在0到1之间，这使得它非常适合用于表示概率。

逻辑回归

损失函数

梯度下降

逻辑回归定义

逻辑函数

逻辑回归使用一种称为逻辑函数（Logistic Function）或S形函数（Sigmoid Function）的函数来建模数据点属于正类别的概率。逻辑函数的数学表示如下：

$$P(Y=1|X)=\frac{1}{1+e^{-z}}$$

其中，$P(Y=1|X)$ 表示给定输入 $X$ 条件下数据点属于正类别的概率，$z$ 是输入特征的线性组合。这个概率值范围在0到1之间，它表示数据点属于正类别的可能性。

线性组合

在逻辑回归中，我们将输入特征的线性组合表示为 $z$：

$$z={\theta }_0+{\theta }_1{X}_1+{\theta }_2{X}_2+\dots +{\theta }_n{X}_n$$

其中，${\theta }_i$ 是模型的参数，$X_i$ 是输入特征。这个线性组合表示了数据点属于正类别的“原始分数”。

模型训练

逻辑回归的目标是找到最佳的参数 $\theta$，使模型能够最好地拟合训练数据并进行准确的分类。为了实现这一点，我们通常使用最大似然估计（Maximum Likelihood Estimation，简称MLE）来估计参数 $\theta$。

MLE的目标是最大化在给定参数 $\theta$ 下观察到训练数据的概率。通过最大化这个概率，我们使模型更可能产生观察到的训练数据，从而提高了模型的性能。

决策边界

一旦模型训练完成并找到最佳参数 $\theta$，我们就可以使用逻辑函数来进行分类。通常，我们会将概率值大于0.5的数据点分为正类别，概率值小于0.5的数据点分为负类别。这个概率阈值通常是可调的。

逻辑回归的决策边界是一个超平面，它将特征空间分成两个区域，每个区域对应一个类别。这个超平面的位置取决于参数 $\theta$。

了解逻辑回归：从原理到实现

逻辑回归是一种常用于分类问题的机器学习算法。它具有简单的原理和实现，同时在各种应用中都有广泛的用途。在本篇博客中，我们将深入了解逻辑回归，包括其原理、实现和应用。

什么是逻辑回归？

逻辑回归是一种二分类算法，用于将输入数据分为两个类别，通常是正类别和负类别。尽管其名称中包含“回归”，但它实际上是一个分类算法，用于估计输入数据属于某一类别的概率。

逻辑回归的原理

逻辑回归的核心思想是使用S形函数（也称为逻辑函数）来建模输入特征和目标类别之间的关系。逻辑函数将输入映射到0到1之间的概率值，表示样本属于正类别的概率。其数学表示如下：

$$P(Y=1|X)=\frac{1}{1+e^{-z}}$$

其中，$P(Y=1|X)$ 表示给定输入 $X$ 条件下样本属于正类别的概率，$z$ 是线性组合的结果，通常表示为：

$$z={\theta }_0+{\theta }_1{X}_1+{\theta }_2{X}_2+\dots +{\theta }_n{X}_n$$

其中，${\theta }_i$ 是模型的参数，$X_i$ 是输入特征。

逻辑回归的实现

逻辑回归的实现通常包括以下步骤：

1. 收集和准备数据：收集样本数据，并对数据进行预处理和特征工程。

2. 定义模型：选择逻辑回归作为模型，并初始化模型参数。

3. 训练模型：使用训练数据集，通过最大似然估计等方法来估计模型参数。

4. 预测和评估：使用训练好的模型对新数据进行预测，并评估模型性能。

5. 超参数调优：根据性能指标调整模型的超参数，如学习率和正则化参数。

逻辑回归的应用

逻辑回归在许多领域都有广泛的应用，包括：

• 医学：用于疾病诊断和预测患者风险。

• 金融：用于信用评分和欺诈检测。

• 自然语言处理：用于文本分类和情感分析。

• 网络安全：用于入侵检测和威胁分析。

代码示例

以下是使用Python和Scikit-Learn库实现的简单逻辑回归代码示例：

from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score# 创建训练数据集和标签
X = [[1.2], [2.4], [3.1], [4.5], [5.0]]
y = [0, 0, 1, 1, 1]# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 创建逻辑回归模型
model = LogisticRegression()# 训练模型
model.fit(X_train, y_train)# 进行预测
y_pred = model.predict(X_test)# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print(f"准确率：{accuracy}")

# 损失函数
def compute_loss(y, y_pred):m = len(y)return -1 / m * np.sum(y * np.log(y_pred) + (1 - y) * np.log(1 - y_pred))# 梯度下降优化参数
def gradient_descent(X, y, theta, learning_rate, num_epochs):m = len(y)losses = []for epoch in range(num_epochs):z = np.dot(X, theta)y_pred = sigmoid(z)gradient = np.dot(X.T, (y_pred - y)) / mtheta -= learning_rate * gradientloss = compute_loss(y, y_pred)losses.append(loss)return theta, losses# 生成示例数据
np.random.seed(0)
X = np.random.randn(100, 3)
y = np.random.randint(0, 2, 100)
print(X)
print(y)
# 添加偏置项（截距项）到特征矩阵
X_b = np.c_[np.ones((100, 1)), X]# 初始化模型参数
theta = np.random.randn(4)# 定义梯度下降参数
learning_rate = 0.1
num_epochs = 1000# 使用梯度下降训练模型
theta, losses = gradient_descent(X_b, y, theta, learning_rate, num_epochs)# 打印最终参数和损失
print("最终参数:", theta)
print("最终损失:", losses[-1])

算法可视化

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score# 创建一个模拟的二分类数据集
X, y = make_classification(n_samples=100, n_features=2, n_classes=2, n_clusters_per_class=1, n_redundant=0, random_state=42)# 将数据集分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 初始化逻辑回归模型
model = LogisticRegression()# 训练模型
model.fit(X_train, y_train)# 预测测试集
y_pred = model.predict(X_test)# 计算模型的准确率
accuracy = accuracy_score(y_test, y_pred)
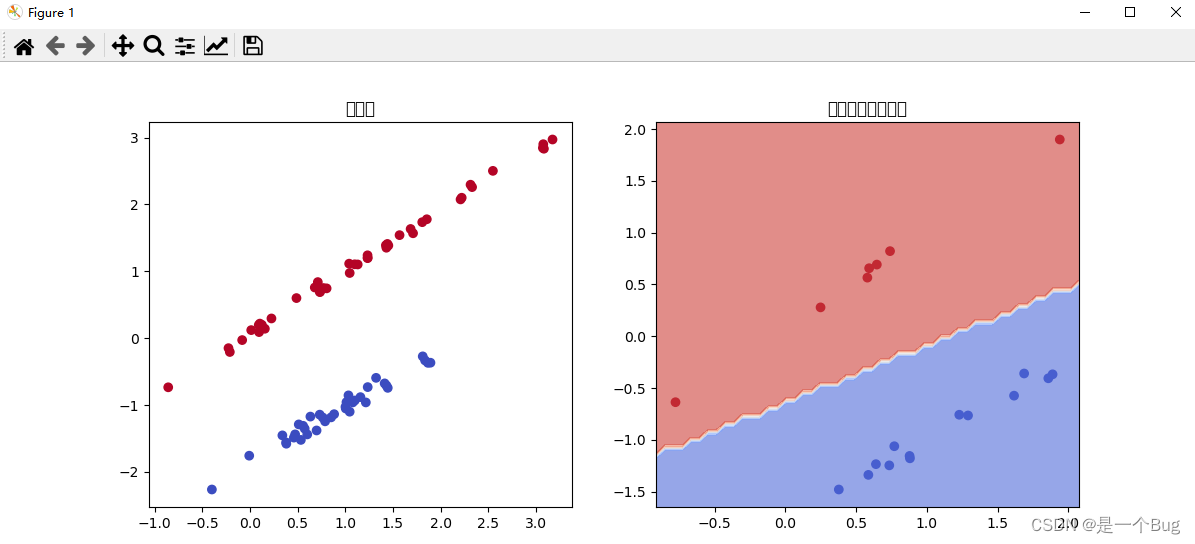
print("模型准确率:", accuracy)# 可视化训练集和测试集以及决策边界
plt.figure(figsize=(12, 5))# 绘制训练集
plt.subplot(1, 2, 1)
plt.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap='coolwarm')
plt.title("训练集")# 绘制测试集以及决策边界
plt.subplot(1, 2, 2)
plt.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap='coolwarm')
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
xx, yy = np.meshgrid(np.linspace(xlim[0], xlim[1], 50),np.linspace(ylim[0], ylim[1], 50))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap='coolwarm', alpha=0.6)
plt.title("测试集和决策边界")plt.show()