使用高斯混合模型进行聚类

一、说明

高斯混合模型（GMM）是一种基于概率密度估计的聚类分析技术。它假设数据点是由具有不同均值和方差的多个高斯分布的混合生成的。它可以在某些结果中提供有效的聚类结果。

二、Kmean算法有效性

K 均值聚类算法在每个聚类的中心周围放置一个圆形边界。当数据具有圆形时，此方法非常有效。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeansnp.random.seed(42)def generate_circular(n_samples=500):X = np.concatenate((np.random.normal(0, 1, (n_samples, 2)),np.random.normal(5, 1, (n_samples, 2)),np.random.normal(10, 1, (n_samples, 2))))return XX = generate_circular()kmeans = KMeans(n_clusters=3, random_state=42)
kmeans_labels = kmeans.fit_predict(X)# boundaries of the cluster spheres
radii = [np.max(np.linalg.norm(X[kmeans_labels == i, :] - kmeans.cluster_centers_[i, :], axis=1))for i in range(3)]# plot
fig, ax = plt.subplots(ncols=2, figsize=(10, 4))ax[0].scatter(X[:, 0], X[:, 1])
ax[0].set_title("Data")ax[1].scatter(X[:, 0], X[:, 1], c=kmeans_labels)
ax[1].scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1],marker='x', s=200, linewidth=3, color='r')
for i in range(3):ax[1].add_artist(plt.Circle(kmeans.cluster_centers_[i, :], radius=radii[i], color='r', fill=False, lw=2))
ax[1].set_title("K Means Clustering")plt.show()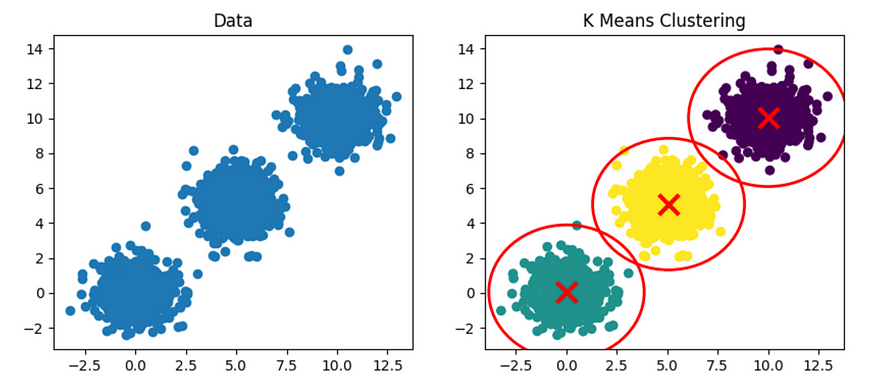

但是，当数据具有不同的形状（如长方形或椭圆形）时，此方法可能无效。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeansnp.random.seed(42)def generate_elliptic(n_samples=500):X = np.concatenate((np.random.normal([0, 3], [0.3, 1], (n_samples, 2)),np.random.normal([2, 4], [0.3, 1], (n_samples, 2)),np.random.normal([4, 6], [0.4, 1], (n_samples, 2))))return XX = generate_elliptic()kmeans = KMeans(n_clusters=3, random_state=42)
kmeans_labels = kmeans.fit_predict(X)
kmeans_cluster_centers = kmeans.cluster_centers_# the radius of each cluster
kmeans_cluster_radii = [np.max(np.linalg.norm(X[kmeans_labels == i, :] - kmeans.cluster_centers_[i, :], axis=1))for i in range(3)]# plot
fig, ax = plt.subplots(ncols=2, figsize=(10, 4))ax[0].scatter(X[:, 0], X[:, 1])
ax[0].set_title("data")ax[1].scatter(X[:, 0], X[:, 1], c=kmeans_labels)
ax[1].scatter(kmeans_cluster_centers[:, 0], kmeans_cluster_centers[:, 1],marker='x', s=200, linewidth=3, color='r')
for i in range(3):circle = plt.Circle(kmeans_cluster_centers[i], kmeans_cluster_radii[i], color='r', fill=False)ax[1].add_artist(circle)
ax[1].set_title("k-means clustering")
plt.xlim(-4, 10) 
plt.ylim(-4, 10)
plt.show()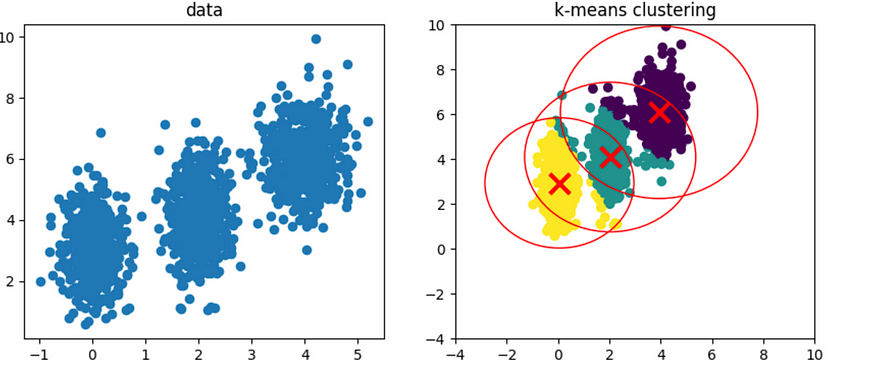

三、比K-mean更进步的GMM

GMM 通过使用高斯分布表示聚类来扩展 K 均值模型。与 K 均值不同，GMM 不仅捕获聚类的均值，还捕获协方差，允许对其椭圆体形状进行建模。为了拟合GMM，我们使用期望最大化（EM）算法，该算法最大化了观察到的数据的可能性。EM 类似于 K 均值，但将数据点分配给具有软概率的聚类，而不是硬赋值。

在高层次上，GMM 结合了多个高斯分布来对数据进行建模。不是根据最近的质心来识别聚类，而是将一组 k 高斯拟合到数据中，并为每个聚类估计平均值、方差和权重等参数。了解每个数据点的参数后，可以计算概率以确定该点属于哪个聚类。

每个分布都按权重因子（π）加权，以考虑聚类中不同的样本数量。例如，如果我们只有来自红色聚类的 1000 个数据点，但来自绿色聚类的 100，000 个数据点，我们将对红色聚类分布进行更严格的权衡，以确保它对整体分布产生重大影响。

组件。源

GMM算法由两个步骤组成：期望（E）和最大化（M）。

第一步称为期望步骤或 E 步骤，包括计算给定模型参数 πk μk 和 σk 的每个数据点 xi∈X 的组件分配 Ck 的期望。

第二步称为最大化步骤或M步骤，它包括最大化E步骤中相对于模型参数计算的期望。此步骤包括更新值 πk、μk 和 σk。

整个迭代过程重复，直到算法收敛，给出最大似然估计。直观地说，该算法之所以有效，是因为知道每个 xi 的分量赋值 Ck 使得求解 πk μk 和 σk 变得容易，而知道 πk μk σk 使得推断 p（Ck|xi）变得容易。

期望步骤对应于后一种情况，而最大化步骤对应于前一种情况。因此，通过在假定固定值或已知值之间交替，可以有效地计算非固定值的最大似然估计值。

算法

使用随机或预定义值初始化平均值（μk）、协方差矩阵（σk）和混合系数（πk）。
计算所有群集的组件分配（Ck）。
使用当前组件分配（Ck）估计所有参数。
计算对数似然函数。
设置收敛标准。
如果对数似然值收敛到特定阈值，或者所有参数都收敛到特定值，请停止算法。否则，请返回到步骤 2。

需要注意的是，此算法保证收敛到局部最优值，但不能确保此局部最优值也是全局最优值。因此，如果算法从不同的初始化开始，则可能会导致不同的配置。

四、python代码

from sklearn.mixture import GaussianMixture

参数：

n_components是聚类数。
covariance_type确定 GMM 使用的协方差矩阵的类型。它可以采用以下值：：每个混合分量都有其通用协方差矩阵。：所有混合分量共享相同的一般协方差矩阵。：每个混料分量都有其对角协方差矩阵。：每个混合分量都有其单个方差值，从而生成球形协方差矩阵。fulltieddiagspherical
tol控制 EM 算法的收敛阈值。当对数可能性的改进低于此阈值时，它将停止。
reg_covar在协方差矩阵的对角线中添加正则化项，以确保计算过程中的数值稳定性。它有助于防止条件不佳或奇异协方差矩阵的潜在问题。
max_iter是 EM 迭代的次数。
n_init控制模型参数的初始化。它可以采用以下值：“kmeans：初始均值是使用 K 均值算法估计的。random“：从数据中随机选择初始均值，并初始化协方差和混合系数。
weights_init手动指定每个组分的初始权重（混合系数）。
means_init手动指定每个分量的初始平均向量。
precision_init手动指定每个分量的初始精度矩阵（协方差矩阵的逆）。

import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
from sklearn.mixture import GaussianMixturedef generate_elliptic(n_samples=500):X = np.concatenate((np.random.normal([0, 3], [0.3, 1], (n_samples, 2)),np.random.normal([2, 4], [0.3, 1], (n_samples, 2)),np.random.normal([4, 6], [0.4, 1], (n_samples, 2))
))return XX = generate_elliptic()# k-means clustering
kmeans = KMeans(n_clusters=3, random_state=0).fit(X)
kmeans_labels = kmeans.labels_# Gaussian mixture clustering
gmm = GaussianMixture(n_components=3, random_state=0).fit(X)
gmm_labels = gmm.predict(X)# Plot the clustering results
fig, axs = plt.subplots(1, 2, figsize=(10, 5))axs[0].scatter(X[:, 0], X[:, 1], c=kmeans_labels)
axs[0].set_title('K-means clustering')axs[1].scatter(X[:, 0], X[:, 1], c=gmm_labels)
axs[1].set_title('Gaussian mixture clustering')plt.show()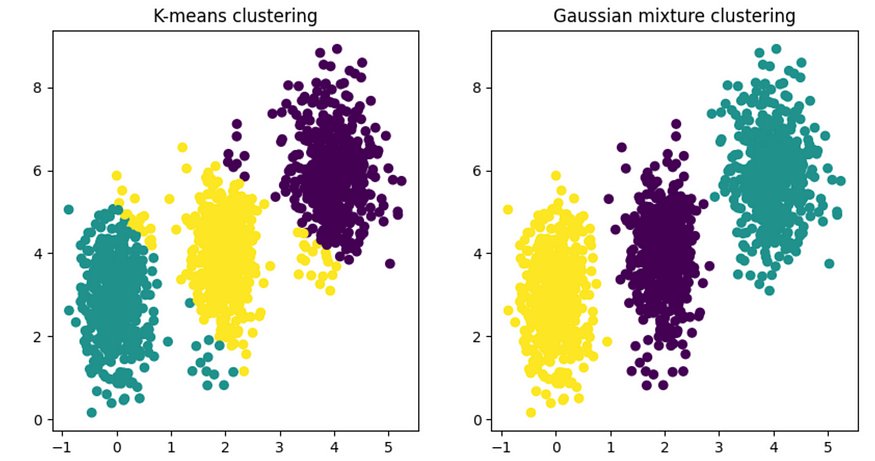

K-means vs Gaussian. Image by the author.

print("Weights: ", gmm.weights_)
print("Means: ", gmm.means_)
print("Covariances: ", gmm.covariances_)
print("Precisions: ", gmm.precisions_)"""
Weights:  [0.33300331 0.33410451 0.33289218]
Means:  [[ 1.98104152e+00  3.95197560e+00][ 3.98369464e+00  5.93920471e+00][-4.67796574e-03  2.97097723e+00]]
Covariances:  [[[ 0.08521068 -0.00778594][-0.00778594  1.01699345]][[ 0.16066983 -0.01669341][-0.01669341  1.0383678 ]][[ 0.09482093  0.00709653][ 0.00709653  1.03641711]]]
Precisions:  [[[11.74383346  0.08990895][ 0.08990895  0.98397883]][[ 6.23435734  0.10022716][ 0.10022716  0.9646612 ]][[10.55160153 -0.07224865][-0.07224865  0.96535719]]]
"""

奥坎·耶尼根