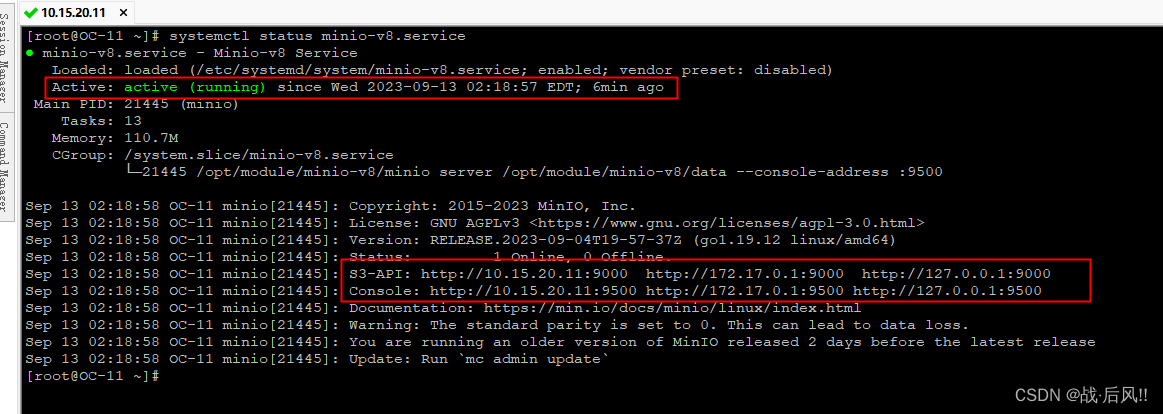
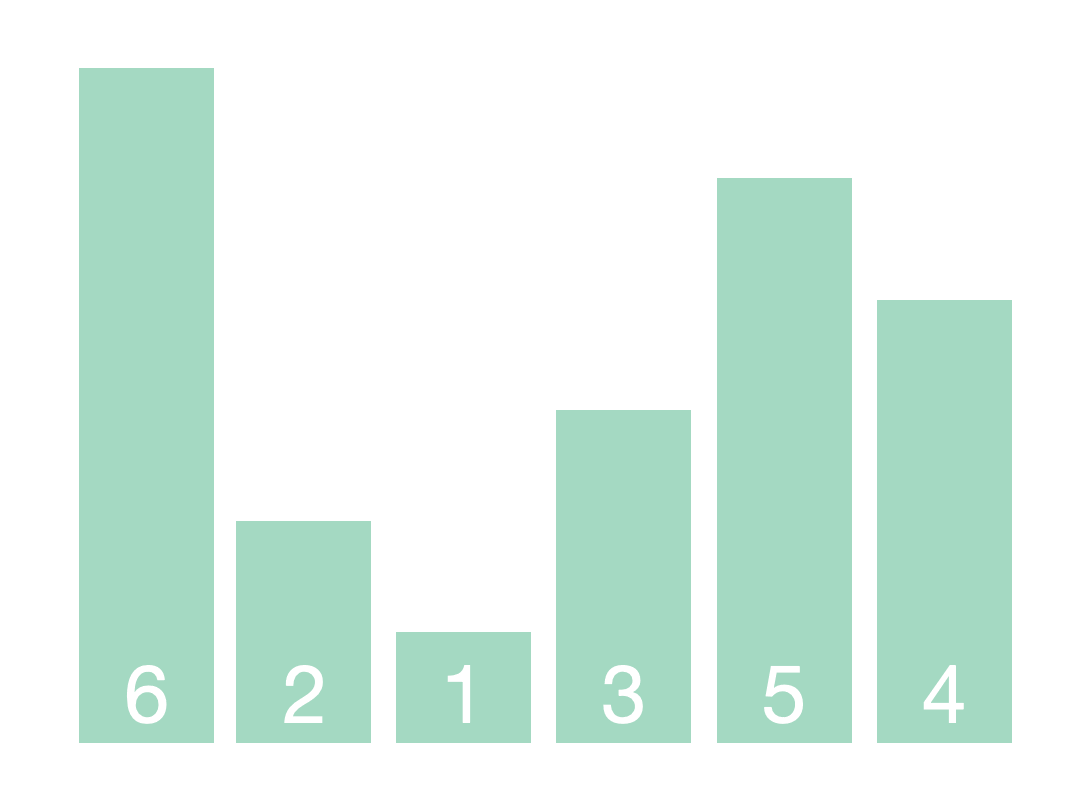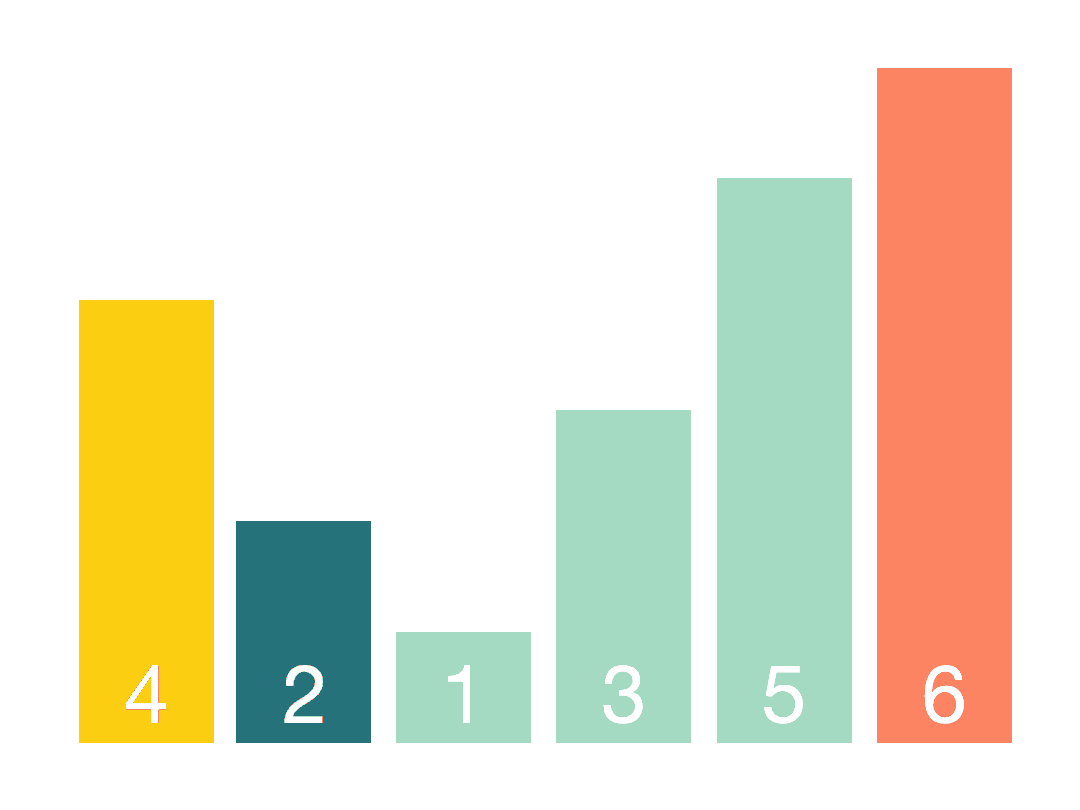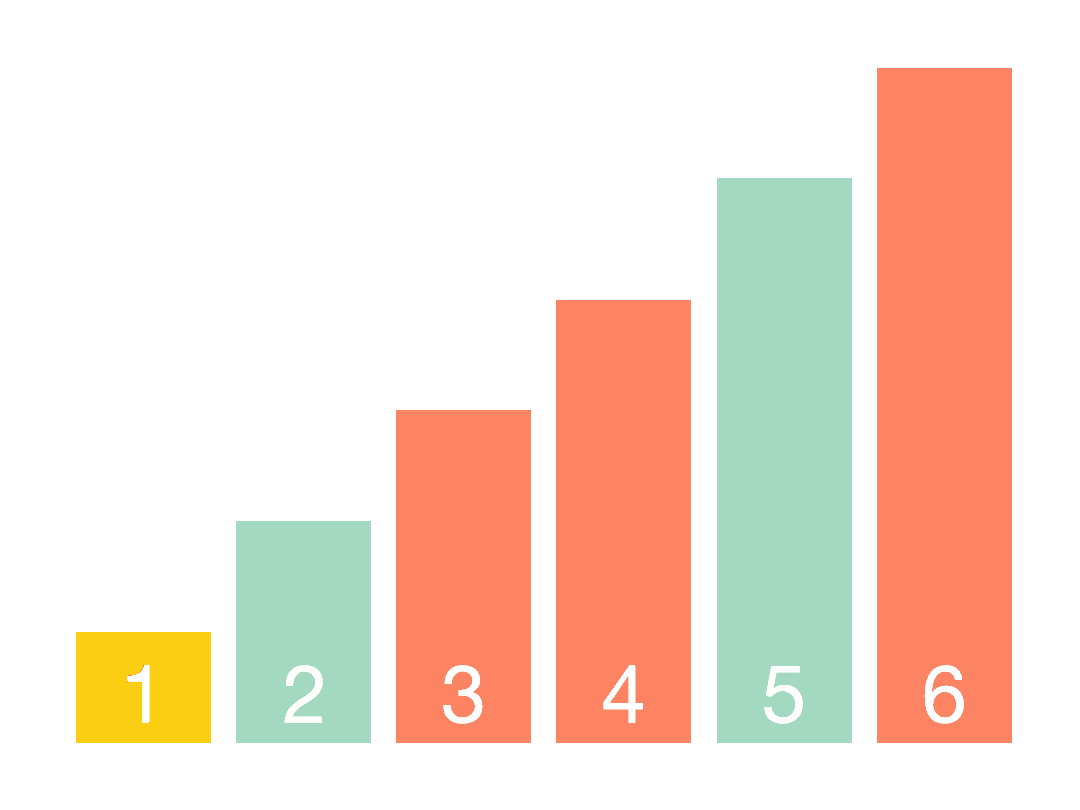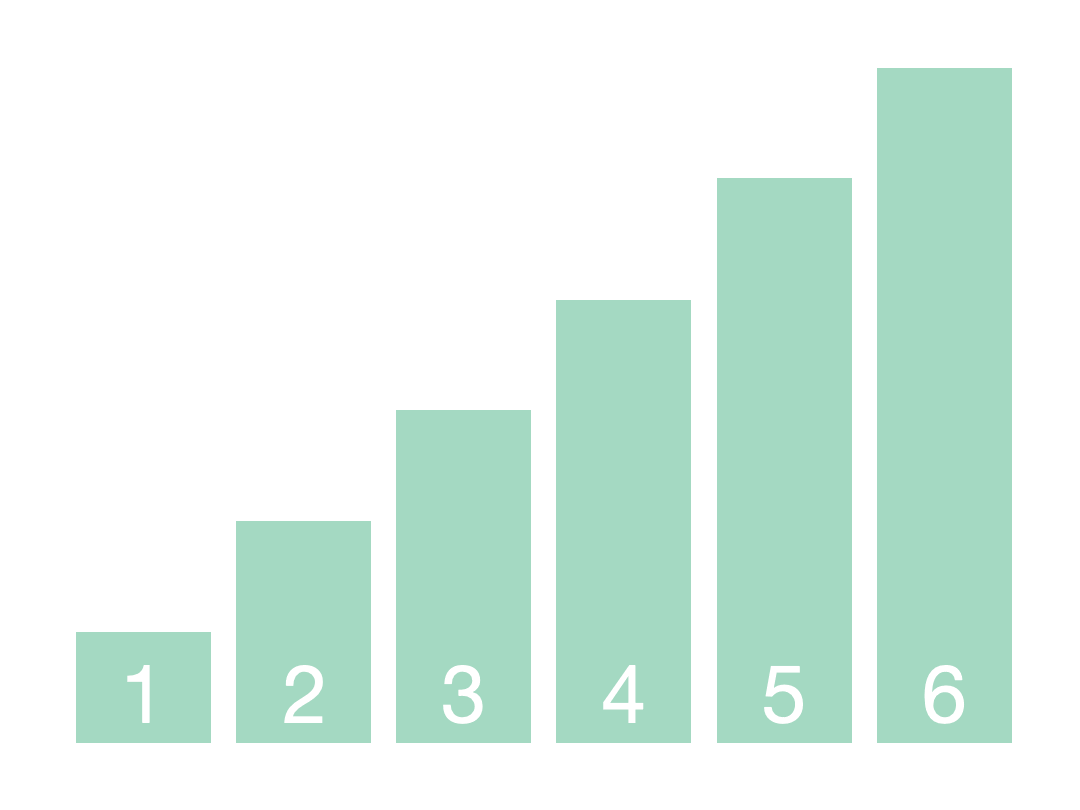想要精通算法和SQL的成长之路 - 受限条件下可到达节点的数目
- 前言
- 一. 相交链表(邻接图和DFS)
前言
想要精通算法和SQL的成长之路 - 系列导航
一. 相交链表(邻接图和DFS)
原题链接
public int reachableNodes(int n, int[][] edges, int[] restricted) {
}
我们读一下题目,我们总结几个核心的点:
- 无向图。
- 受限节点。
- 题目用一个二维数组代表图。
针对第一个点和第三个点:我们用何种方式通过二维数组来构建出一个无向图?
使用邻接图。在Java当中,邻接图可以用下面一个模板来完成:
List<Integer>[] adj = new List[n];
// 初始化每个数组
for (int i = 0; i < n; i++) {adj[i] = new ArrayList<>();
}
for (int[] edge : edges) {adj[前继节点].add(后继节点);
}
那么由于本题目又特意声明了它是一个无向图,我们前后顺序换一下再存储一次即可:
adj[前继节点].add(后继节点);
adj[后继节点].add(前继节点);
针对第二点:受限节点。我们用一个一维数组,代表每个元素是否受限,下标即是对应的元素值:
boolean[] limits = new boolean[n];
for (int i : restricted) {limits[i] = true;
}
有了这些数据,我们就可以通过DFS去递归遍历这颗树:
- 我们指定对应的元素 0 作为根节点,向后继节点递归。
- 同时因为无向的关系,我们在递归节点的时候,需要做判断,当前节点并不是父节点,满足条件才可往深层递归。否则就会出现死循环。
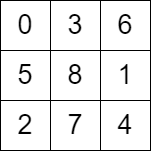
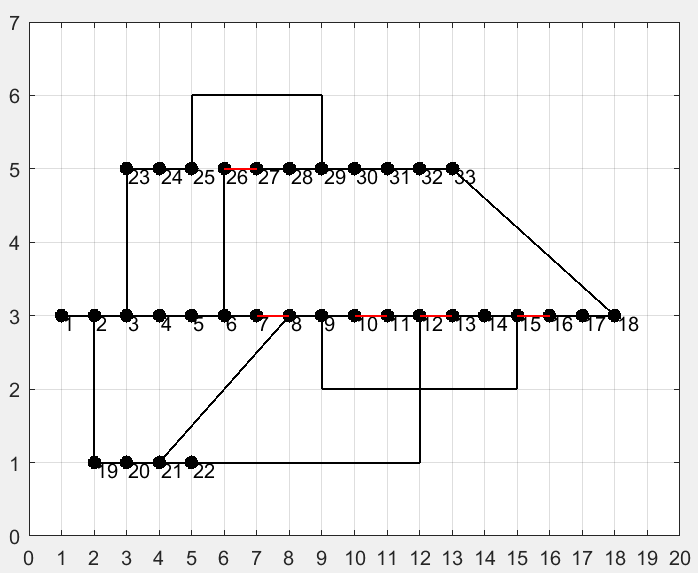
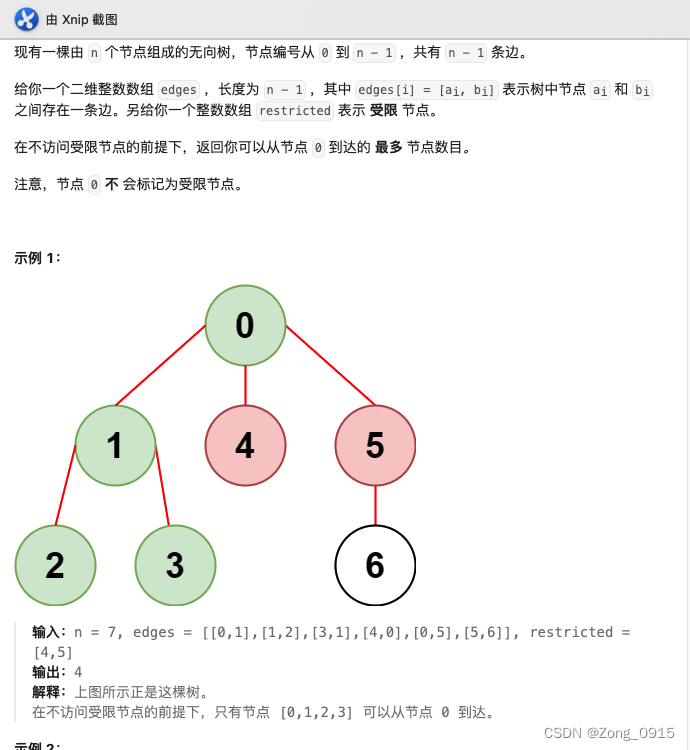
例如:以上图的案例,最终的无向图数据部分如下:
- 0–>1,4,5。
- 1->0,1,3
死循环逻辑如下:
- 第一层:倘若当前节点为1的时候,根据顺序深层递归。递归节点0。
- 第二层:当前遍历节点为0,发现0的相邻节点有1,开始递归节点1。回到第一步。
- 第三层…
因此我们在dfs递归的时候需要有两个参数:
- 当前节点。
- 当前节点的父节点。
同时我们用一个全局变量count代表递归的数量(即是题目返回要求)
void dfs(int root, int pre) {count++;for (int node : adj[root]) {if (!limits[node] && node != pre) {dfs(node, root);}}
}
最终完整代码如下:
public class Test2368 {int count = 0;List<Integer>[] adj;boolean[] limits;public int reachableNodes(int n, int[][] edges, int[] restricted) {// 邻接图数据构建adj = new List[n];for (int i = 0; i < n; i++) {adj[i] = new ArrayList<>();}for (int[] edge : edges) {adj[edge[0]].add(edge[1]);adj[edge[1]].add(edge[0]);}// 构建受限节点数组limits = new boolean[n];for (int i : restricted) {limits[i] = true;}// 开始递归,从根节点0开始,父节点不存在,我们传一个-1dfs(0, -1);return count;}void dfs(int root, int pre) {count++;// adj[root] 就是与 当前节点 所有的相邻节点for (int node : adj[root]) {// 非受限节点并且当前节点并不是父节点的时候,继续往下递归if (!limits[node] && node != pre) {dfs(node, root);}}}
}